एक अचल त्रिभुजाकार ब्लॉक पर दो गुटके स्थित है| ये गुटके ब्लॉक पर लगी एक घिरनी एक घिरनी पर से होकर जाती है डोरी से बँधे है| प्रत्येक गुटके तथा ब्लॉक के बीच स्थितिज घर्षण गुणांक 0.28 तथा गतिज घर्षण गुणांक 0.25 है|
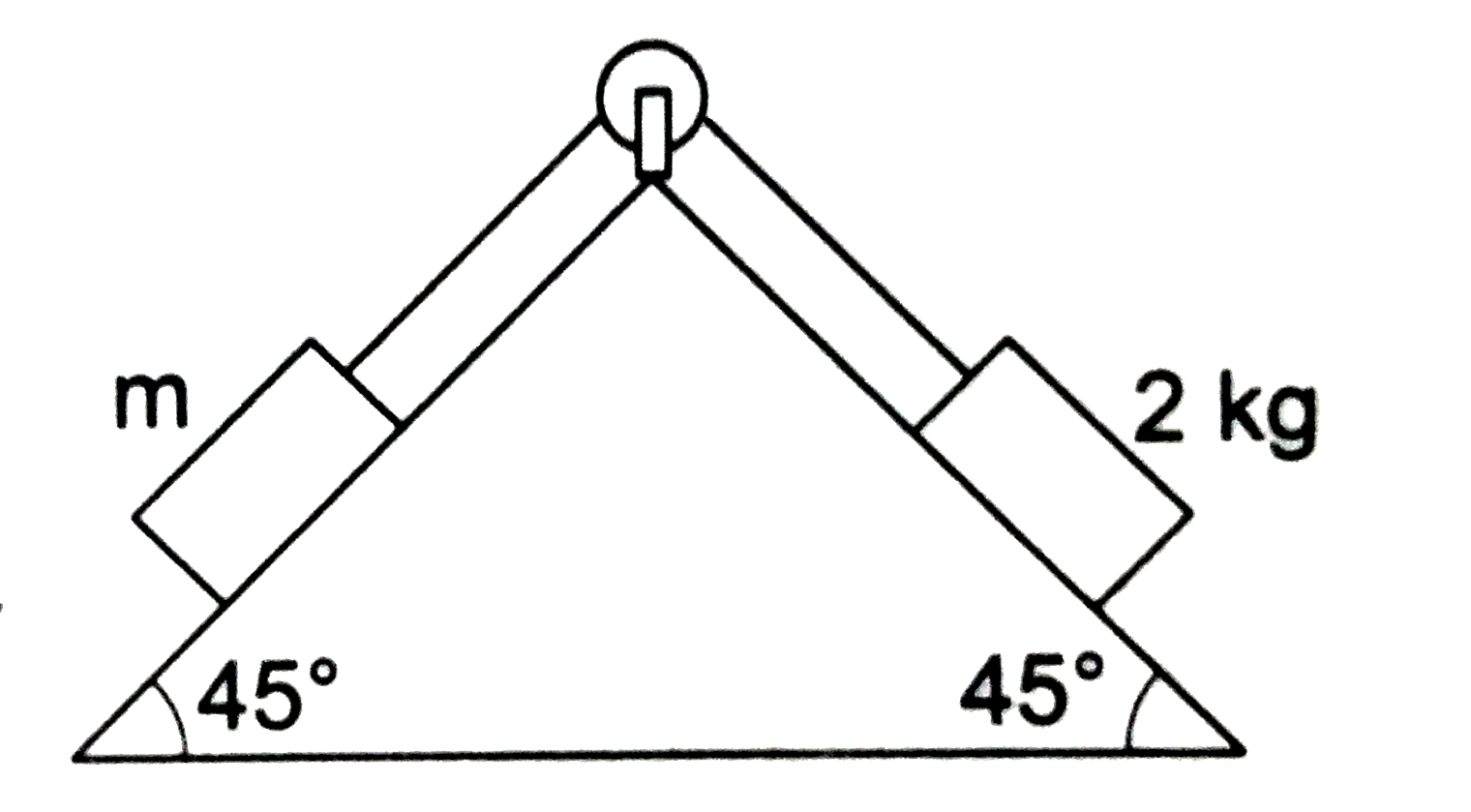
(a) द्रव्यमान m का न्यूनतम और अधिकतम मान निकालें ताकि गुटके स्थिर रहे| मान लें की इन दोनों स्थितियों में दोनों गुटकों पर सीमांत घर्षण लग रहे है|
(b) यदि m का मान न्यूनतम के बराबर रखा जाये और 2 kg के गुटके को धीरे से सतह पर निचे की और जरा-सा चलाकर छोड़ दिया जाए, तो गुटकों के त्वरण का परिमाण निकालें|
(a ) जब m अपने न्यूनतम मान पर है तब 2kg का गुटका निचे की और तथा m द्रव्यमान वाला गुटका ऊपर की और फिसलने की प्रवृति रखेगा|
2kg के गुटके पर लगते बल में दिखाए गए है| यहाँ M =2kg है| चूँकि गुटका स्थिर है ,उसपर लगनेवाले सभी बलों का योग शून्य होगा|
(##HCVHINPHYCOPC09SLV011_S01.png width=80%><br>सतहकेलंबवतघटकलेनेपर,<br> " "N=Mcos45^(@) =(Mg)/(sqrt(2))<br>सतहकेसमांतरघटकलेनेपर<br> " "T+ f= Mg sin 45^(@) =(Mg)/(sqrt(2))<br>या " "T+ mu_s N=( Mg)/( sqrt(2))<br>या " "T=(Mg)/(sqrt(2)) (1-mu_s ) " "...(i) <br>अबmद्रव्यमानवालेगुटकेकोदेखे∣∣इसपरलगतेबलमेंदिखायगएहै∣∣<br>सतहकेलंबवतघटकलेनेपर<br> " "N'=mg cos 45^(@) =(mg)/( sqrt(2))<br>सतहकेसमानांतरघटकलेनेपर<br> T= mg sin 45^(@) + f'=(mg)/(sqrt(2))+ mu _s N' =(mg)/( sqrt(2) ) +mu_s (mg)/(sqrt(2))<br>या T= (mg)/( sqrt(2)) (1+ mu_s)" "...(ii)<br>समीकरण(i)तथा(ii)से<br> " "m( 1+mu_s) =M (1-mu_s) " "...(iii)<br>या " "m=( 1-mu_s)/(1+mu_s) M=(1-0.28)/(1+ 0.28) xx2kg =( 9)/(8) kg .<br>गुटकोंकोसंतुलनमेंबनायेरखनेकेलिएतथाmकाअधिकतममानज्ञातकरनेकेलिएहमसमीकरण(iii)मेंहीmu_ s =- 0.28रखसकतेहै∣∣ऐसाइसलिएकीअधिकतमmरखनेपरयहगुटकानीचेकीऔरतथा2kgकागुटकाऊपरकीऔरसरकनेकाप्रयासकरेगा∣∣अतःदोनोंजगहसीमांतघर्षणकीदिशाएंउल्टजाएँगी∣गणितकरनेमें mu_s काचिन्हबदलनेसेइसस्थितिकेसमीकरणमिलजातेहै∣<br>अतः m=(1+mu_s) /(1-mu_s)M =( 1+ 0.28)/( 1-0.28) xx 2kg =(32)/(9) kg .<br>(b)अबm= (9)/(8) kg लियागयाहैऔर2kgकेगुटकेकोनीचेकीऔरचलाकरछोड़दियागयाहै∣∣अबगतिजघर्षणकामकरेंगे∣∣यदित्वरणकामानaहोतो<br> " "Mg sin 45^(@) -T -f =Ma <br>या " "(Mg)/(sqrt(2)) -T -( mu_kMg)/( sqrt(2)) =Ma" "...(iv) <br>तथाचित्रसे<br> " "T -mg sin 45^(@) -f =ma <br>या " "T-(mg)/(sqrt(2))-mu_k (mg)/(sqrt( 2)) =ma " "...(v) <br>समीकरण(iv)तथा(v)कोजोड़नेपर,<br> (Mg)/(sqrt(2)) (1-mu_k) -(mg)/(sqrt(2)) (1+ mu_k) =(M+m) a <br>या a =( M( 1-mu_k) -m (1+mu_k ))/( sqrt(2) (M +m) ) g <br> " " = (2xx0.75-(9)/(8) xx1.25)/( sqrt(2) (2+ (9)/(8))) g <br> " "= 0.31m//s^(2)
Topper's Solved these Questions
- BOOK - HC VERMA HINDICHAPTER - घर्षण EXERCISE - उदाहरण5videos
घर्षण
- BOOK - HC VERMA HINDICHAPTER - घर्षण EXERCISE - विचार हेतु प्रश्न13videos
घर्षण
- BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - अभ्यास के प्रश्न50videos
गोलीय सतहों पर अपवर्तन
- BOOK - HC VERMA HINDICHAPTER - घूर्णन गतिEXERCISE - अभ्यास के प्रश्न12videos
घूर्णन गति
Similar Questions
400 ग द्रव्यमान की एक वस्तु एक टेबुल पर चल रही है| टेबुल वस्तु पर 3.0N का घर्षण बल लगाती है|(a ) टेबुल द्वारा वस्तु पर लगाय गए कुल बल ऊर्ध्वाधर से कोण निकालें|(b ) इस कुल बल का परिमाण निकालें | g=10m/s2 माने|
View Solutionदैनिक जीवन में प्रयुक्त अधिकांश सतहों के बीच घर्षण गुणांक का मान 1 से कम होता है| क्या सदैव यह आवश्यक है की घर्षण गुणांक का मान 1 से कम ही हो?
09:58View Solutionचित्र में दिखाई गई सतह के दाहिने काँच ( n = 1.5) तथा बाएँ हवा हैं । सतह की त्रिज्या 20 cm हैं तथा उससे 25 cm दूरी पर हवा में एक बिंदुस्त्रोत रखा हैं । प्रतिबिंब का स्थान बताएँ ।
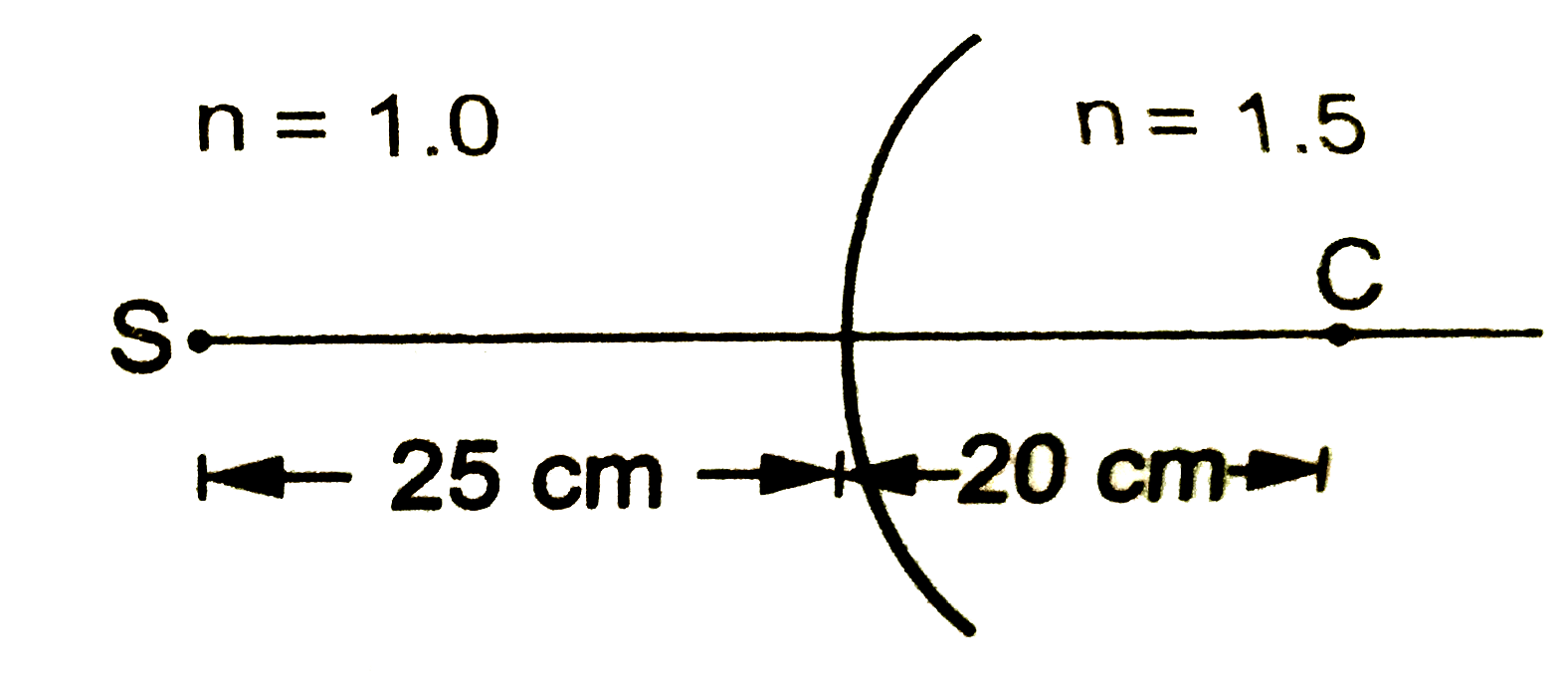 04:01View Solution
04:01View Solutionएक पहिया अपने अक्ष के परितः एकसमान कोणीय त्वरण से घूर्णन कर रहा है | विरामावस्था से प्रारंभ करके यह 4 s में 100 चक्कर/सेकंड चाल प्राप्त कर लेता है | पहिये का कोणीय त्वरण ज्ञात करें | इन चार सेकंडो में पहिये द्वारा तय किया गया कोण भी ज्ञात करें |
08:00View Solutionचित्र में प्रदर्शित ब्लॉकों के बीच घर्षण गुणांक μ है, किन्तु फर्श घर्षणरहित है|
04:32View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
03:50View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।04:26View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
04:29View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
05:40View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
06:39View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
02:42View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
46:57View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
48:07View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionघर्षण रहित नत तल पर रखे गुटके की गति
View Solution

