3 cm किनारे वाली लकड़ी का एक घन एक बरतन में रखे पानी में तैरता है | यह घन बरतन में रखे दो प्लेटों के बिच में है (चित्र 24. W4) जिसके कारण इसकी सतहें क्षैतिज तथा ऊर्ध्वाधर तलों में रहती है | इस बरतन की पेंदी में एक ऊर्ध्वाधर स्प्रिंग जुड़ा है | घन की निचली सतह स्प्रिंग के ऊपरी सिरे को छूती है | इस घन के ऊपर अधिकतम कितने भार की वस्तु रखी जा सकती है ताकि वह पानी में न भींगे ? लकड़ी का घनत्व =800kg/m3, स्प्रिंग नियतांक =50N/m,g=10m/s2.
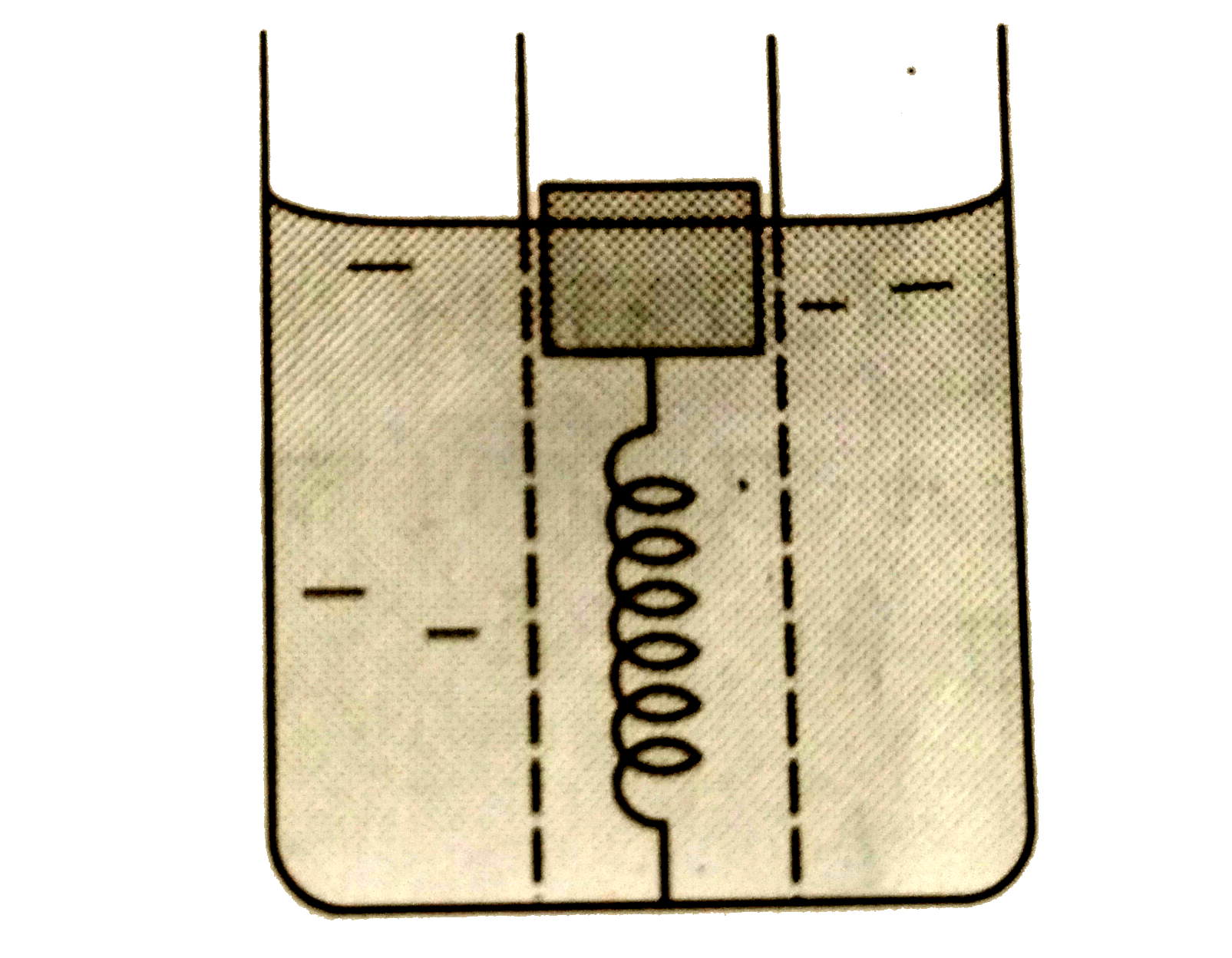
प्रारंभ में घन द्वारा विस्थापित पानी का भार = घन का भार | यदि इसकी h ऊंचाई पानी में हो, तो
h×L2×ρwater×g=L3×ρwood×g
या h×L×ρ woodρ water=(3cm)×8001000=2.4cm.
घन का भार =(3cm)2×800kgm3×10ms2=0.22N.
जब अधिकतम भार रख दिया जाए तो घन पूरी तरह पानी में चला जाएगा | अर्थात, घन x=(3−2.4)cm=0.6cm निचे जाएगा और स्प्रिंग भी इतनी लंबाई से दाब जाएगा | इस स्थिति में घन तथा उसपर रखे भार पर लगते बलों को सोचें | ये बल है,
(a) कुल भार W, निचे की ओर
(b) स्प्रिंग द्वारा बल F1, ऊपर की ओर
(c) उत्प्लावन बल F2, ऊपर की ओर
W=0.22N+W',
जहाँ W' घन के ऊपर रखी गई वस्तु का भार है |
F1=kx=(50Nm)×(0.6cm)=0.3N
तथा F2=(3cm)3×1000kgm3×10ms2=0.27N
संतुलन के लिए,
W=F1+F2
या 0.22N+W'=0.3N+0.27N
या W'=0.35N.
अतः, अधिकतम 35 g की वस्तु घन पर रखी जा सकती है |
Topper's Solved these Questions
- तरल पदार्थों कि भौतिकीBOOK - HC VERMA HINDICHAPTER - तरल पदार्थों कि भौतिकीEXERCISE - विचार हेतु प्रश्न
18 Videos
- तरल पदार्थों कि भौतिकीBOOK - HC VERMA HINDICHAPTER - तरल पदार्थों कि भौतिकीEXERCISE - सटीक उत्तरवाले प्रश्न I
19 Videos
- तरल पदार्थों कि भौतिकीBOOK - HC VERMA HINDICHAPTER - तरल पदार्थों कि भौतिकीEXERCISE - अभ्यास के प्रश्न
39 Videos
- डोरियों पर अप्रगामी तरंगेंBOOK - HC VERMA HINDICHAPTER - डोरियों पर अप्रगामी तरंगेंEXERCISE - अभ्यास के प्रश्न
21 Videos
- द्रवों का प्रवाहBOOK - HC VERMA HINDICHAPTER - द्रवों का प्रवाहEXERCISE - अभ्यास के प्रश्न
11 Videos
Similar Questions
जब कोई आपको नुकीली सुई चुभाता, है तब आपको बहुत दर्द होता है | पर यदि वह आपको उतने ही बल से एक डंडा चुभाए, तो आप आसानी से उसे सह जाते हैं | ऐसा क्यों ? दर्द होने का दाब से क्या संबंध है ?
View Solutionचित्र 24.Q1 में दिखाए गए तीनों बरतनों की पेंदी के क्षेत्रफल समान है | बराबर आयतन के द्रव इन तीनों में डाले जाते हैं | पेंदी पर बल
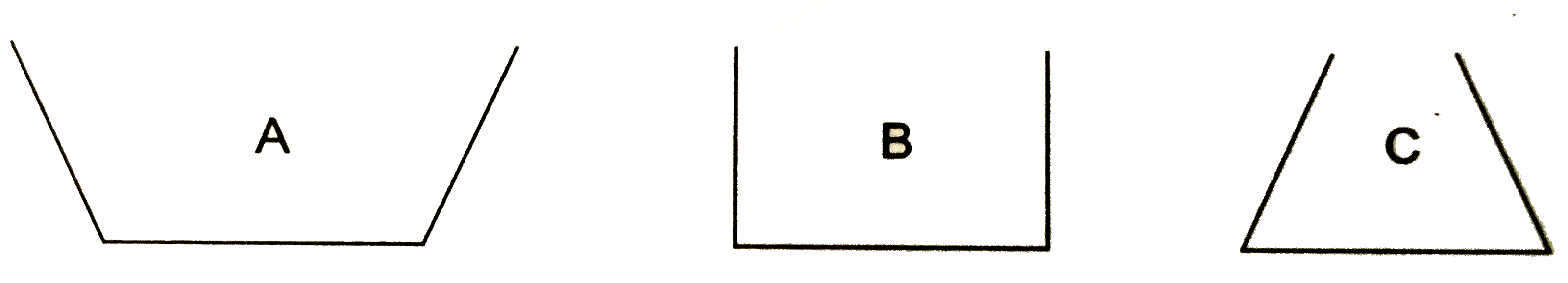
View Solutionएक घर की छत पर रखे पानी की टैंक में पानी की सतह नल की सतह से 4 m ऊपर है | नल के पानी का दाब (वायुमंडलीय दाब के सापेक्ष) निकाले जब वह बंद हो | क्या यह कहना आवश्यक है कि नल बंद हो ? g=10m/s2 ले |
View Solutionयदि 1m लंबी रस्सी पर अनुप्रस्थ तरंगिका की चाल 60m/s और इसे दोनों किनारों पर बांधकर रखा जाए, तो इसकी मूल आवृत्ति कितनी होगी ?
View Solutionउत्तराखंड प्रान्त के देवप्रयाग में अलकनंदा ओर भागीरथी नदियाँ आपस में मिलकर गंगा नदी बनकर आगे बढ़ती है । मान ले कि अलकनन्दा कि चौड़ाई 12 m , भागीरथी कि चौड़ाई 8 m तथा गंगा कि चौड़ाई वह 16 m है । अलकनंदा तथा भागीरथी नदियों में पानी के औसत वेगो को क्रमशः 20 km/h तथा 16 km/h माने । नदियों कि गहराई को समान मानते हुए तथा श्यानता को अनदेखा करते हुए गंगा का औसत वेग निकाले ।
View Solutionएक घनाकार सन्दूक के आयतन कि गणन में प्रतिशत त्रुटि ज्ञात कीजिये यदि घन कि कोर कि लम्बाई में त्रुटि 5 प्रतिशत रहती है।
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View SolutionA cube is placed inside a cone of radius 20cm and height 10cm, one of its face being on the base of the cone and vertices of opposite face touching the cone. What is the length (in cm) of side of the cube? एक घन को एक शंकु जिसकी त्रिज्या 20 से. मी. तथा ऊँचाई 10 से.मी. है, के अंदर रखा जाता है, उसको एक सतह शंकु के आधार कौर ओर है तथा विपरीत सतह के शीर्ष शंकु का स्पर्श कर रहे है। घन की भुजा लम्बाई (से. मी. में) क्या है ?
View SolutionA solid sphere has a radius 21 cm. It is melted to form a cube. 20% material is wasted in this process. The cube is melted to form hemisphere. In this process 20% material is wasted. The hemisphere is melted to form two spheres of equal radius. 20% material was also wasted in this process. What is the radius (in cm) of each new sphere?
एक ठोस गोले की त्रिज्या 21 से.मी. है। इसे पिघलाकर एक घन बनाया जाता है । इस प्रकिया में 20% सामग्री व्यर्थ हो जाती है। घन को पिघलाकर एक अर्धगोला बनाया जाता है। इस प्रकिया में 20% सामग्री व्यर्थ हो जाती है। अर्धगोला को पिघलाकर दो समान त्रिज्या वाले दो गोले बनाये जाते है। इस प्रकिया में भी 20% सामग्री व्यर्थ हो गई थी। प्रत्येक नए गोले की त्रिज्या (से.मी. में) क्या. है?
View SolutionThe volume of a cube is 216 cm^3 . What is the area of one face of the cube? किसी घन का आयतन 216 cm^3 है | इस घन के एक फलक का क्षेत्रफल ज्ञात करें |
View SolutionA sphere is inscribed in a cube. What is the ratio of the volume of the cube to the volume of the sphere?
एक गोले को किसी घन में डाला गया है | घन के आयतन तथा गोले के आयतन में अनुपात ज्ञात करें |
View SolutionThe volume of a cube is 343 cm^3 . The edge of cube is: एक घन का आयतन 343 cm^3 है। घन का किनारा है:
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
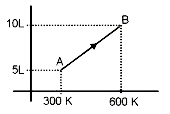
View Solution
