Question

एक लंबी तनी हुई डोरी पर एक तरंग धनात्मक -दिशा में चल रही है । इसका समीकरण है
$y=y_0{e}^{-{(\frac{x}{\lambda }-\frac{t}{T})}^2}$
जहाँ $y_0=4mm$, $T=1.0s$ तथा $\lambda =4cm$ है । (a) तरंग की चाल बताएँ| (b) समय t के साथ $x=0$ के कण के विस्थपन के लिए फलन $f\left(t\right)$ बताएँ । (c ) $t=0$ पर डोरी के विभिन्न कणों के विस्थापन के लिए फलन $g\left(x\right)$ बताएँ । (d) $t=0$ पर डोरी की सकल बताने के लिए ग्राफ खींचे तथा (e) t = 5 s पर डोरी की शक्ल बताने के लिए ग्राफ खींचें ।

Explanation

(a) `y = y_(0)e^(-(t/T-x/lambda)^(2)) = y_(0)e^(- 1/(lambda^(2))(x-(lambdat)/(T))^(2))`
`y = f(x - upsilont)` की तुलना करने पर,
`upsilon = (lambda)/(T) = (4 cm)/(1.0 s) = 4 cm//s`
(b) `x = 0` रखने पर ,
`y = y_(0)e^(-(t/T)^(2)) = (4 mm) e^((t/(1.0s))^(2))`
(c ) `t = 0` रखने पर ,
`y = y_(0)e^(-(x/lambda)^(2)) = (4mm) e^(-(x/(4cm))^(2))`
(d) `t = 0` पर डोरी की शक्ल नीचे चित्र में दिखाए गए ग्राफ से मिलेगी ।

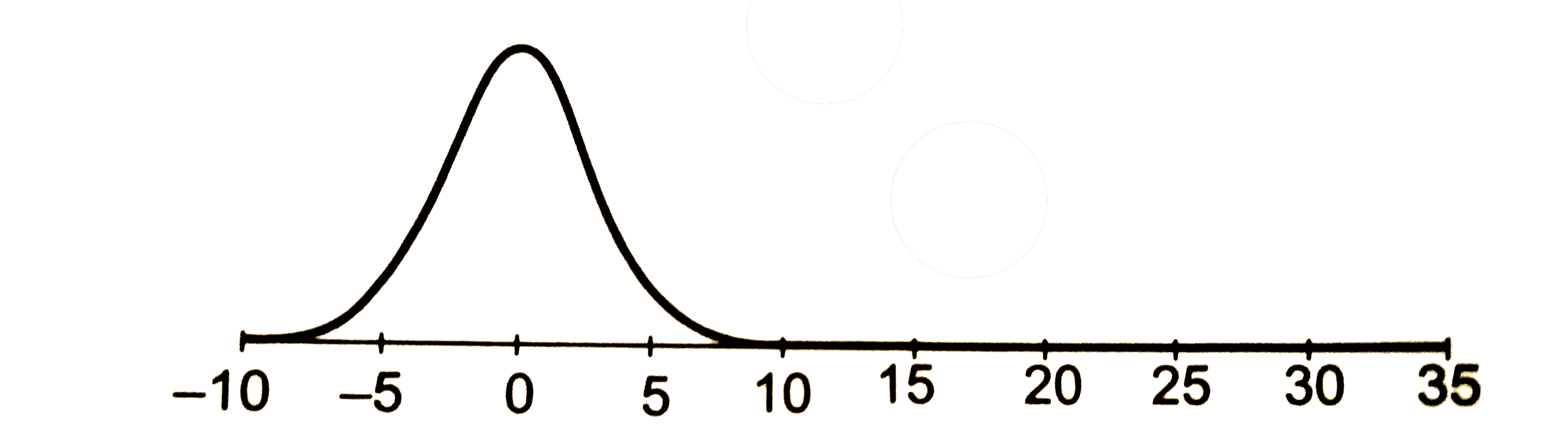
(e) `t = 5s` पर
`y = y_(0) e^(-(t/T - x/lambda)^(2)) = (4 mm) e^(-(x/4cm - (5s)/(1s))^(2))`
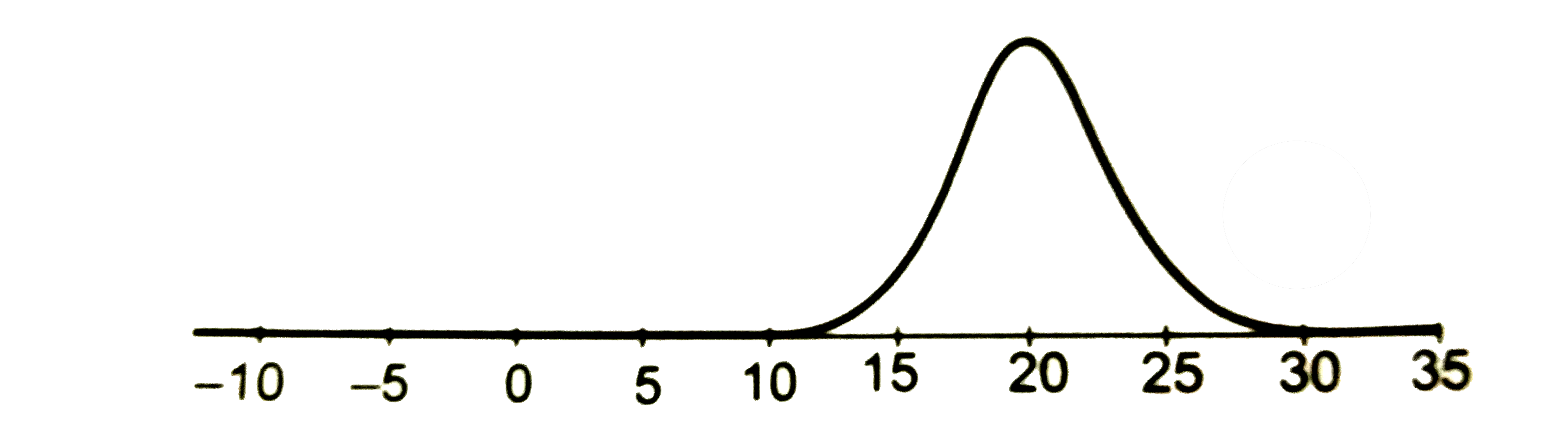
` (4mm)e^(-((x-20 cm)/(4cm))^(2)`
डोरी की यह शक्ल चित्र में दिखाई गई है । यह ठीक वैसी ही है जैसी `t = 0` पर थी । अंतर् सिर्फ इतना है कि `t = 0` पर यह शक्ल `x = 0` पर केंद्रित है , जबकि `t = 5s` पर यह`x= 20 cm` पर केंद्रित है । तरंग 5s में `20 cm` आगे बढ़ गई है।