15 cm फोकस -दूरी का एक उत्तल लेंस तथा 20 cm फोकस - दूरी का एक अवतल दर्पण इस प्रकार रखे गए हैं कि उनके मुख्य अक्ष एक ही हैं । एक बिंदुस्त्रोत S मुख्य अक्ष पर लेंस से 12cm दूरी पर रखा गया हैं । यह पाया जाता हैं कि सारे परावर्तन एंव अपवर्तन के बाद किरणें अक्ष के समानांतर हो जाती हैं । लेंस तथा दर्पण के बीच की दूरी निकालें ।
बिंदुस्त्रोत S से आती किरणें लेंस से निकलने के बाद I1 पर प्रथम प्रतिबिंब बनाती हैं । इस भाग के लिए ,
u = -12 cm , f = 15 cm . अतः 1v=1u+1f
1−12cm+115cm
−160cm
या v = - 60 cm .
यहाँ ऋणात्मक चिह्र बताता हैं कि प्रतिबिंब लेंस के बायीं ओर बना हैं जैसा कि चित्र में दिखाया गया हैं ।
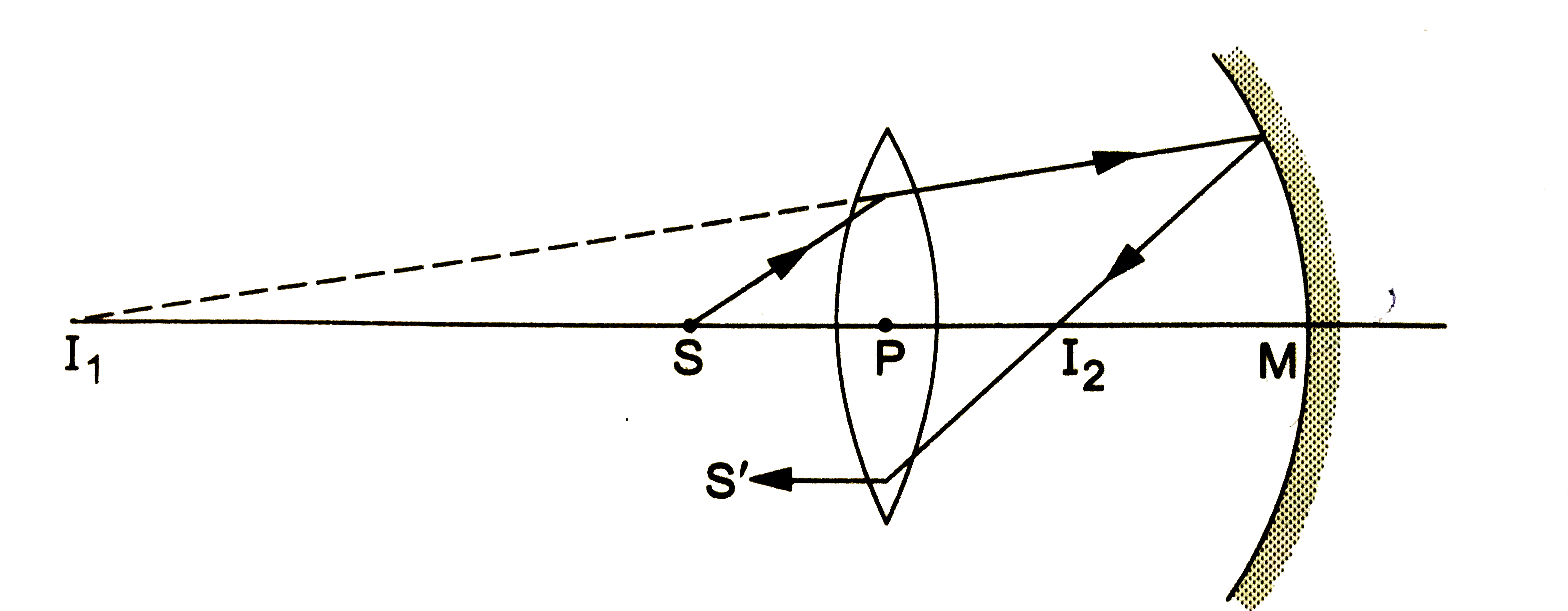 लेंस से निकलती किरणें , जो I1 पर ( पीछे बढ़ाने पर ) कटती हैं , अवतल दर्पण पर आपतित होती हैं । अतः , अवतल दर्पण के लिए I1 वस्तु का स्थान हैं । यदि दर्पण की लेंस से दूरी x cm हो तो दर्पण से बने प्रतिबिंब I2 के लिए ,
लेंस से निकलती किरणें , जो I1 पर ( पीछे बढ़ाने पर ) कटती हैं , अवतल दर्पण पर आपतित होती हैं । अतः , अवतल दर्पण के लिए I1 वस्तु का स्थान हैं । यदि दर्पण की लेंस से दूरी x cm हो तो दर्पण से बने प्रतिबिंब I2 के लिए ,
u = -(60 + x ) cm , f = -20 cm .
अतः , दर्पण के सूत्र 1v+1u=1f
1v=1f−1u=1−20cm−1−(60+x)cm
= −(40+x)cm(20cm)(60+x)cm
या v=−(20cm)(60+x)cm(40+x)cm. .
अवतल दर्पण व्दारा परिवर्तित किरणें I2 पर मिलेंगी । ये किरणें पुनः लेंस पर आपतित होती हैं और लेंस के मुख्य अक्ष के समानांतर होकर निकलती हैं । स्पष्ट है कि I2 को लेंस के फोकस पर होना होगा । अर्थात् , लेंस से I2 की दूरी 15 cm होगी ।
PM=PI2+I2M
या x cm = 15 cm + 20(60+x)40+x cm
या x( 40 + x) = 15(40 + x ) + 20 ( 60 + x)
या x2+5x−1800=0
अतः , x = 40 या - 45 .
चूँकि लेंस तथा दर्पण के बीच की दूरी - 45 cm नहीं हो सकती हैं , अतः , यह दूरी 40 cm हैं ।
Topper's Solved these Questions
- BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - अभ्यास5videos
गोलीय सतहों पर अपवर्तन
- BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - विचार हेतु प्रश्न6videos
गोलीय सतहों पर अपवर्तन
- BOOK - HC VERMA HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - अभ्यास के प्रश्न40videos
गुरुत्वाकर्षण
- BOOK - HC VERMA HINDICHAPTER - घर्षण EXERCISE - अभ्यास के प्रश्न30videos
घर्षण
Similar Questions
चित्र में दिखाई गई परिस्थिति में वस्तु O के प्रतिबिंब का स्थान निर्धारित करें । बिंदु C दोनों माध्यमों की उभयनिष्ठ (COMMON) गोलीय सतह का वक्रता - केंद्र हैं ।
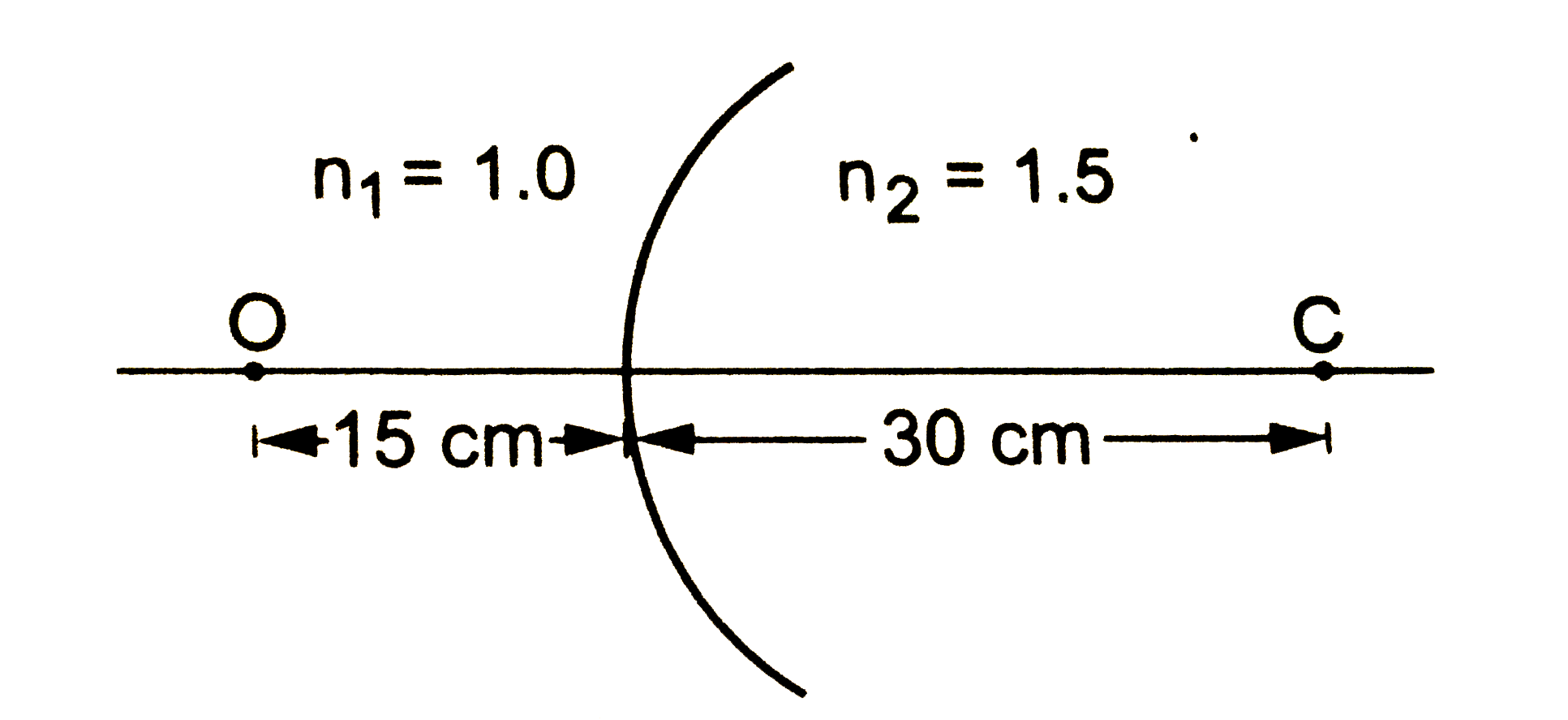 08:36View Solution
08:36View Solutionएक अपारदर्शी टयूब के अंदर एक लेंस फिट किया हुआ हैं , प्रकाश की एक समानांतर बीम ट्यूब में प्रवेश करती हैं और अपसारी ( divergent) बीम के रुप में ट्यूब के अंदर का लेंस हैं ?
53:16View Solution10 kg द्रव्यमान की दो गोलाकार गेदे एक – दूसरे से 10 cm दूर रखी गई है। इनके बीच लगनेवाले गुरूत्वीय बल ज्ञात करें।
04:32View Solutionएक खुरदरे (rough ) क्षैतिज तल पर फिसल रही वस्तु 4.0m/s2 अवमंदन से गतिशील है|वस्तु तथा तल के बीच गतिज घर्षण गुणांक का मान निकालें|
04:45View Solutionएक बिंदु वस्तु एक काँच जिसका अपवर्तनांक (μs=32) है, से बने 20 सेमी फोकस दूरी वाले उत्तल लेन्स से 30 सेमी की दूरी पर रखी है। वस्तु का अन्तिम प्रतिबिमब अनन्त पर बनेगा यदि
03:50View Solutionलेंस तथा इसके अवयव || उत्तल लेंस द्वारा प्रतिबिम्ब बनने के नियम || अवतल लेंस द्वारा प्रतिबिम्ब बनने के नियम
04:26View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
48:30View Solutionएक परवलय का अक्ष X-अक्ष के अनुदिश है। यदि इसके शीर्ष तथा नाम नाभि , X-अक्ष कि धनात्मक दिशा में मूलबिंदु से क्रमशः 2 तथा 4 कि दुरी पर हैं , तो इनमें से कौन - सा बिन्दु इस परवलय पर स्थित नहीं है ?
55:43View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
01:21:11View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
55:31View Solutionलेंस की क्षमता | लेंस की फोकस दूरी तथा क्षमता में सम्बन्ध
05:35View Solutionलेंस की फोकस दूरी की निर्भरता|लेंस सूत्र तथा संयुग्मी फोकस
38:09View Solutionसंपर्क में रखे दो पतले लेंसों की संयुक्त फोकस दूरी|उत्तल लेंस तथा समतल दर्पण का संयोजन#!#लेंसों के उपयोग
48:24View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
36:41View Solutionएक लेंस 10 सेमी दूरी पर रखी वस्तु का तीन गुना बड़ा आभासी प्रतिबिम्ब बनाता है। लेंस की प्रकृति, फोकस दूरी तथा प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
View SolutionBoard Special|प्रकाश - परावर्तन तथा अपवर्तन#!#उत्तल तथा अवतल दर्पण के अनुप्रयोग #!#दर्पण सूत्र
01:38View Solution

