Plot the graph of the function f(x)=limt→0(2xπtan−1xt2)
Video Solution
|
Answer
Step by step video & image solution for Plot the graph of the function f(x)=lim_(t->0)((2x)/pitan^(- 1)x/(t^2)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The graph of the function f(x)=Limt→0(2xπcot−1xt2), is
A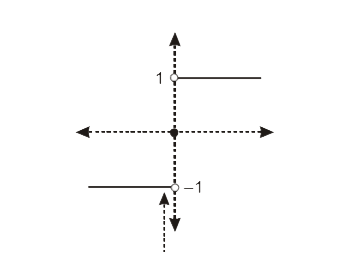 B
B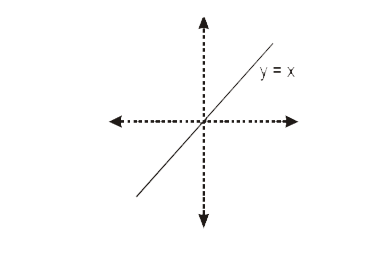 C
C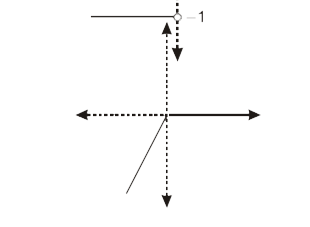 D
D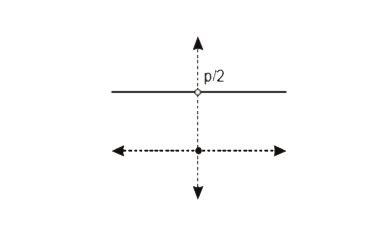
The interval in which the function
f(x)=∫x0(tt+2−1t)dtwill be non- increasing isA(−2,−1]∪(0,3]B(−2,−1]∪[0,3]C(-2,-1]cup [0,2]D(−2,−1]∪(0,2]If the function f(x) satisfies limx→1f(x)−2x2−1=π, then limx→1f(x) is equal to
A1B2C0D3
If f(x)=limt→0[2xπ.tan−1(xt2)],then f(1) is …….
View SolutionFor the function f(x)=2. Find limx→1f(x)
View SolutionFind the derivative with respect to x of the following functions :
(a) F(x)=∫2x0sintt dt ,
(b) f(x)=∫0x√1+t4dt
View SolutionIf the graph of the function y=f(x) has a unique tangent at point (ea,0) (not vertical, non-horizontal) on the graph, then evaluate limx→ea(1+9f(x))−tan(f(x))2f(x).
View SolutionLet f(x) be differentiable on the interval (0,∞) such that f(1)=1 and limt→xt2f(x)−x2f(t)t−x=1 for each x>0. Then f(x)=
View Solution