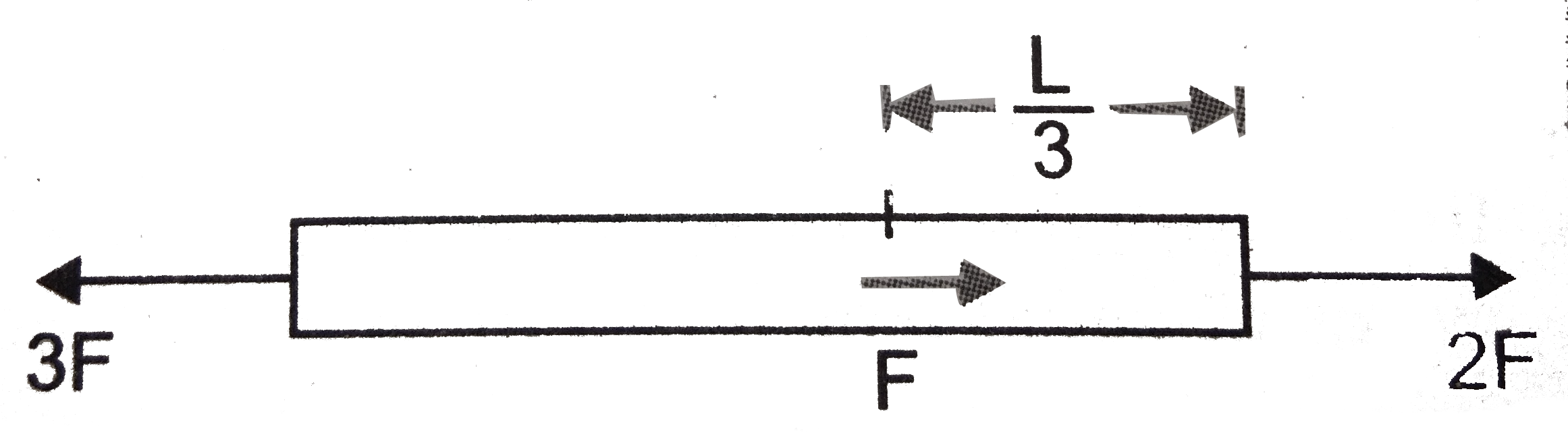
A uniform elastic rod of cross sectional area A, natural length L and Young's modulus Y is placed on a smooth horizontal surface. Now two horizontal forces (F and 3F) directed along the length of rod and in opposite direction act at two of its ends as shown. After the rod has acquired steady state, the extension of rod will be -
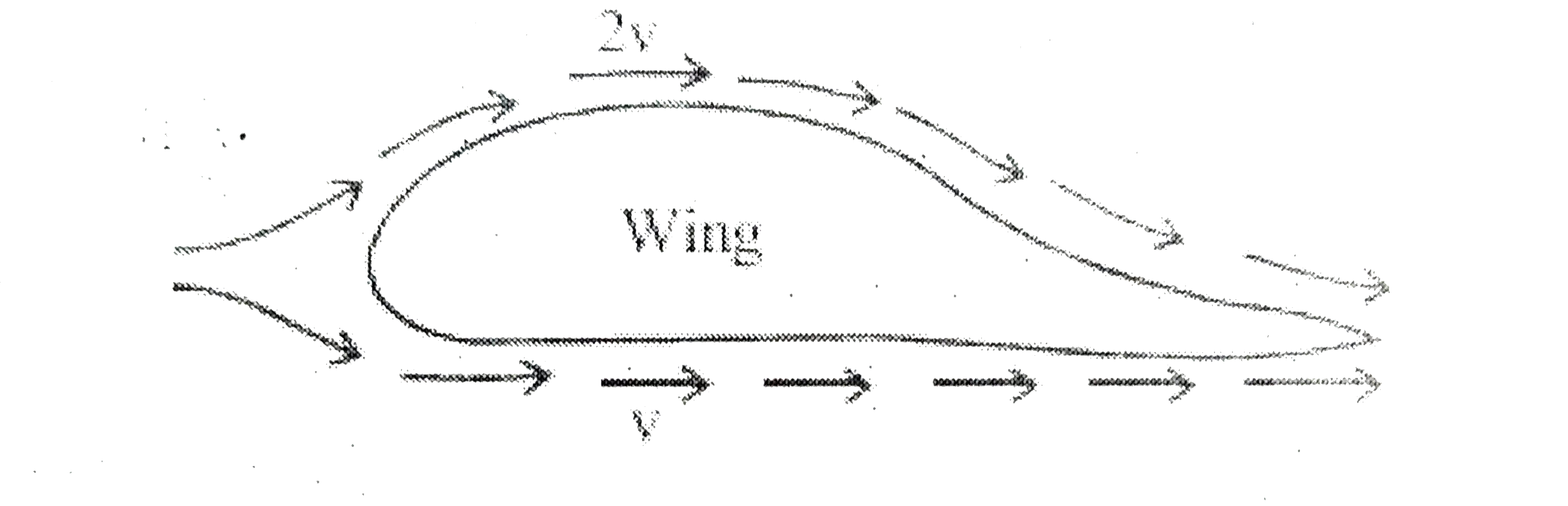
12ρv2A
rhov^(2)A
32ρv2A
2ρv2A
The correct Answer is:C
P+12ρv21=P2+12ρv22
ΔP=12ρ(v22−v21)
ΔP=12ρ[(2v)2−v2]
ΔP=32ρv3
Topper's Solved these Questions
Similar Questions
Two blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
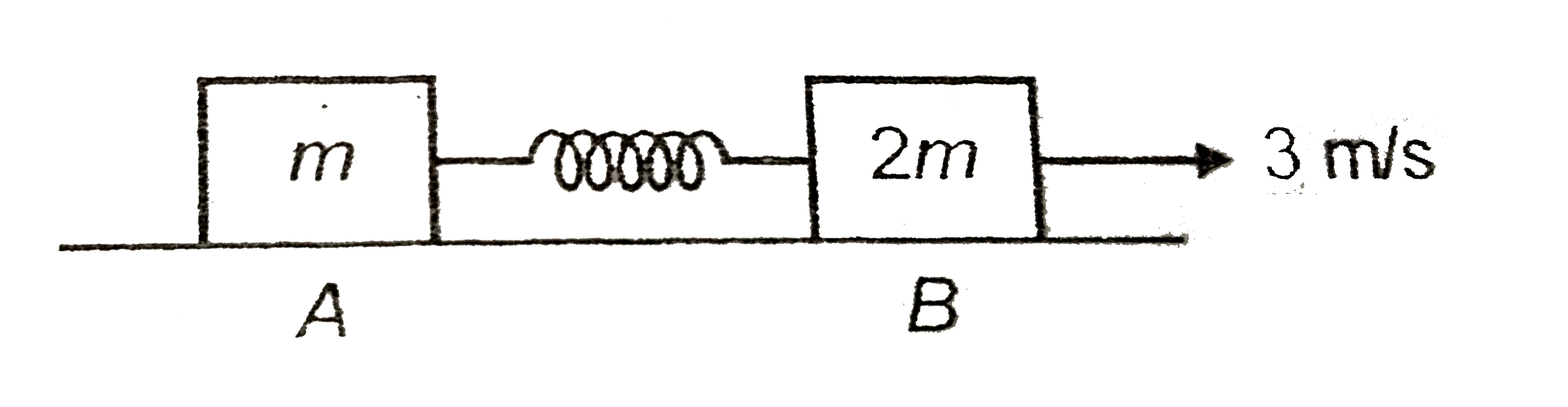
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View Solution
Knowledge Check

A uniform elastic rod of cross section area A natural length L and Young's modulus Y is placed on a smooth horizontal surface. Now two horizontal forces (of magnitude F and 3F) directed along the length of rod and in opposite direction act at two of its ends as shown . After the rod has acquired steady state, the extension of the rod will beA2FYALB4FYALCFYALD3F2YALA uniform plank of Young's modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross section of the plank is A. The compressive strain on the plank in the direction of the force is
AF/AYB2F/AYC12(F/AY)D3F/AYA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elongation in section PQ of rod and section QR of rod isA1:1B3:5C5:7D1:2
A uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is

View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View Solution
