Find four consecutive terms in an A.P. whose sum is 46 and the product of the 1st and the 3rd is 56. The terms are in ascending order.
Let four consecutive termsin an A.P. be and .
From the first condition.
………1
From th second condition
.....(Substituting the value of )
....(Multiplying both the sides by )
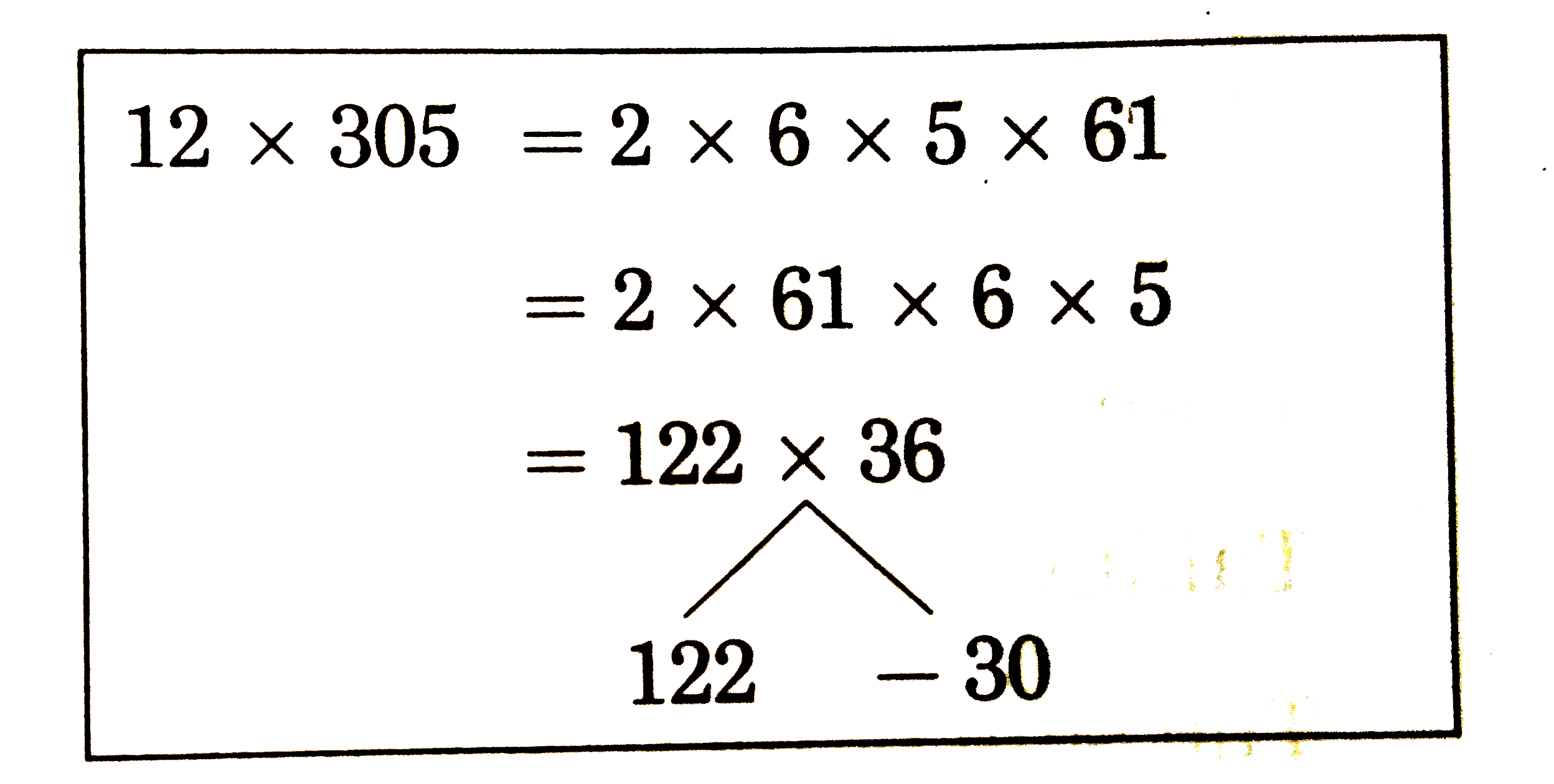
brgt or
or
or
The terms are in ascending order is unacceptable.
The required terms are 4,9,14, and 19.
Topper's Solved these Questions
- CHALLENGING QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE
22 Videos
- BOARD'S QUESTION PAPER : MARCH 2019BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - BOARD'S QUESTION PAPER : MARCH 2019EXERCISE - QUESTION
30 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
Similar Questions
Knowledge Check
The sum of four consecutive terms in A.P. is 36 and the ratio of product of the first and fourth is to be the product of the second and the third is 9:10 . Find the largest of the numbers :
A9B10C8D12
Find three consecutive terms in A.P.whose sum is 9 and the product of their cubes is 3375
View SolutionFind four consecutive terms in an A.P. whose sum is −8 and sum of third and fourth term is 8.
View SolutionFind four consecutive term in an A.P. such that the sum is -54 and the sum of the first and the third terms is −30.
View SolutionFind four consecutive terms in an A.P. Whose sum is 72 and the ratio of the product of the 1st and the 4th terms to the product of the 2nd and 3rd terms is 9 : 10.
(a) Let the four consecutive terms be a - 3d, a - d, a + d, a + 3d.
(b) Using the first condition, find the value of a.
(c) Using the second condition, find the value of d and hence the numbers.
View SolutionFind the three terms in AP, whose sum is 36 and product is 960.
View SolutionThe sum of three consecutive terms of an A.P. is 30 and their product is 360. Find the terms.
View SolutionThe sum of three consecutive terms of an A.P. is 9 and the sum of their squares is 35. Find the terms.
View Solution
