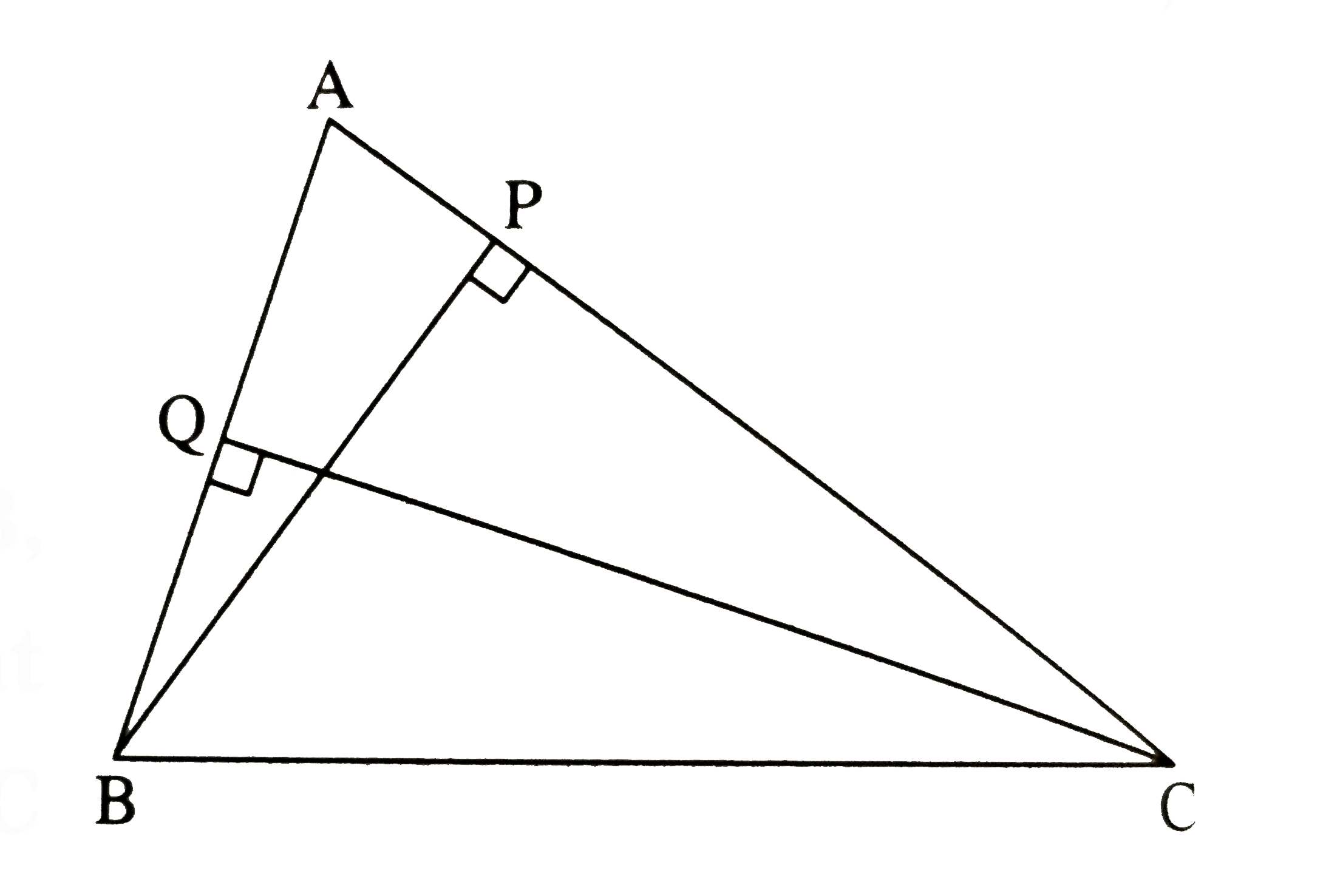
In the adjoining figure, BP⊥AC, CQ⊥AB, A−P−C, A−Q−B. Complete the following activity to Prove ΔAPB~ΔAQC.
In ΔAPB and ΔAQC
∠APB=□∘…….(1)
∠AQC=□∘……..(2)
∴∠APB≅∠AQC…....(□)
∴ΔAPB~ΔAQC......(□)

In ΔAPB and ΔAQC
∠APB=90∘…….(1)
∠AQC=90∘……..(2)
∴∠APB≅∠AQC…....(common angle)
∴ΔAPB~ΔAQC......("AA" test of similarity)
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.4 (3 mark each)8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)3videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.2 (1 mark each)5videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ABCD is a square. M is the midpoint of AB and PQ⊥CM. Which of the following statements is not true ?
 AAM = MBBCP = CQCCP = CBDPM = MQ
AAM = MBBCP = CQCCP = CBDPM = MQ - Question 2 - Select One
In the following figure, PQRS is a square. M is the mid-point of PQ and AB⊥RM. Then, which of the following is false?
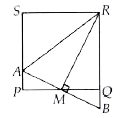 AAM=MBBRA=RBCΔRMA=ΔRMBDΔRAM≅ΔRMB
AAM=MBBRA=RBCΔRMA=ΔRMBDΔRAM≅ΔRMB
In the following figure, square ABCD is inscribed in the sector C-BXD IS 20 cm. Complete the following activity to find the area of shaded region
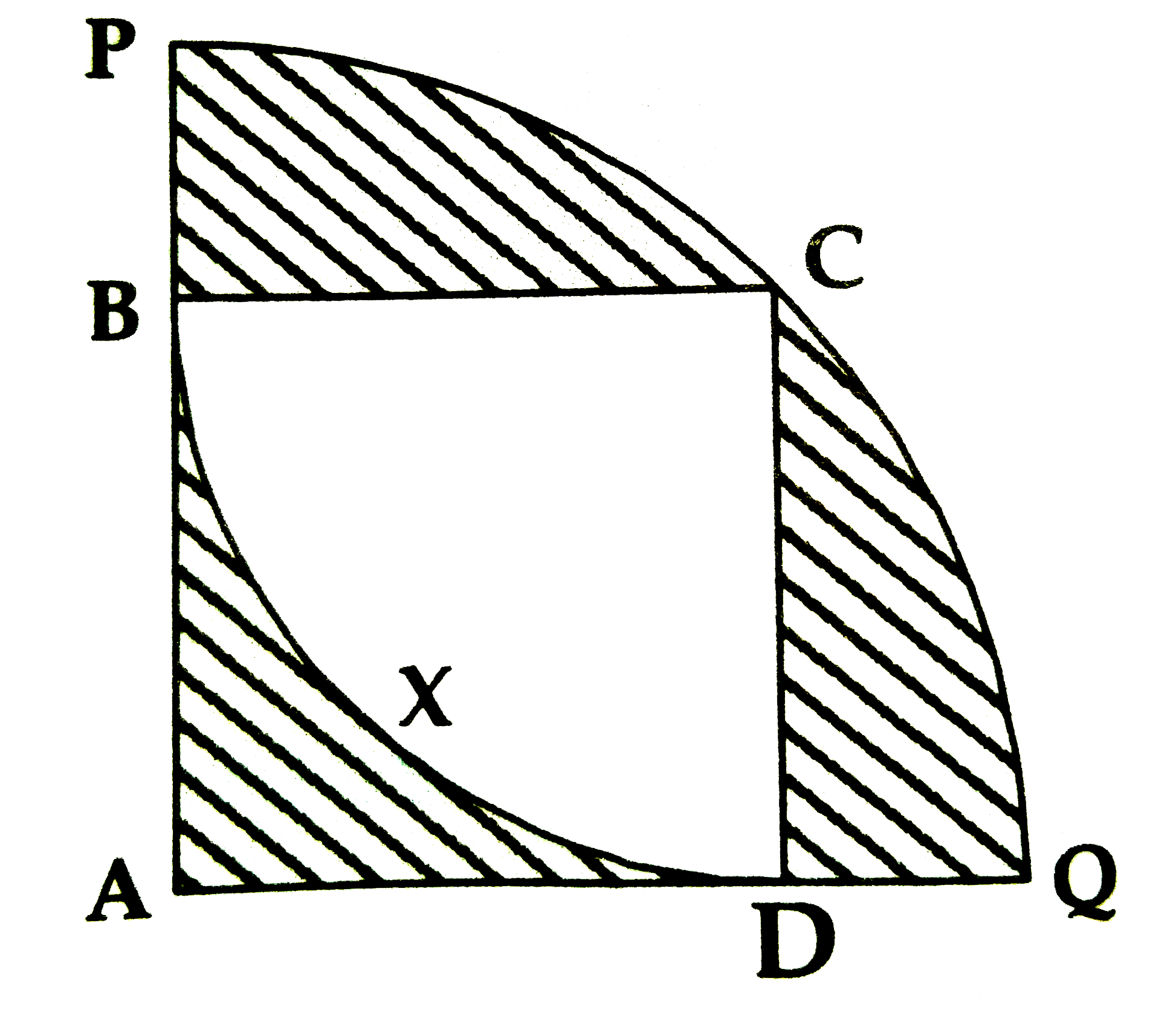 View Solution
View SolutionIn the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.
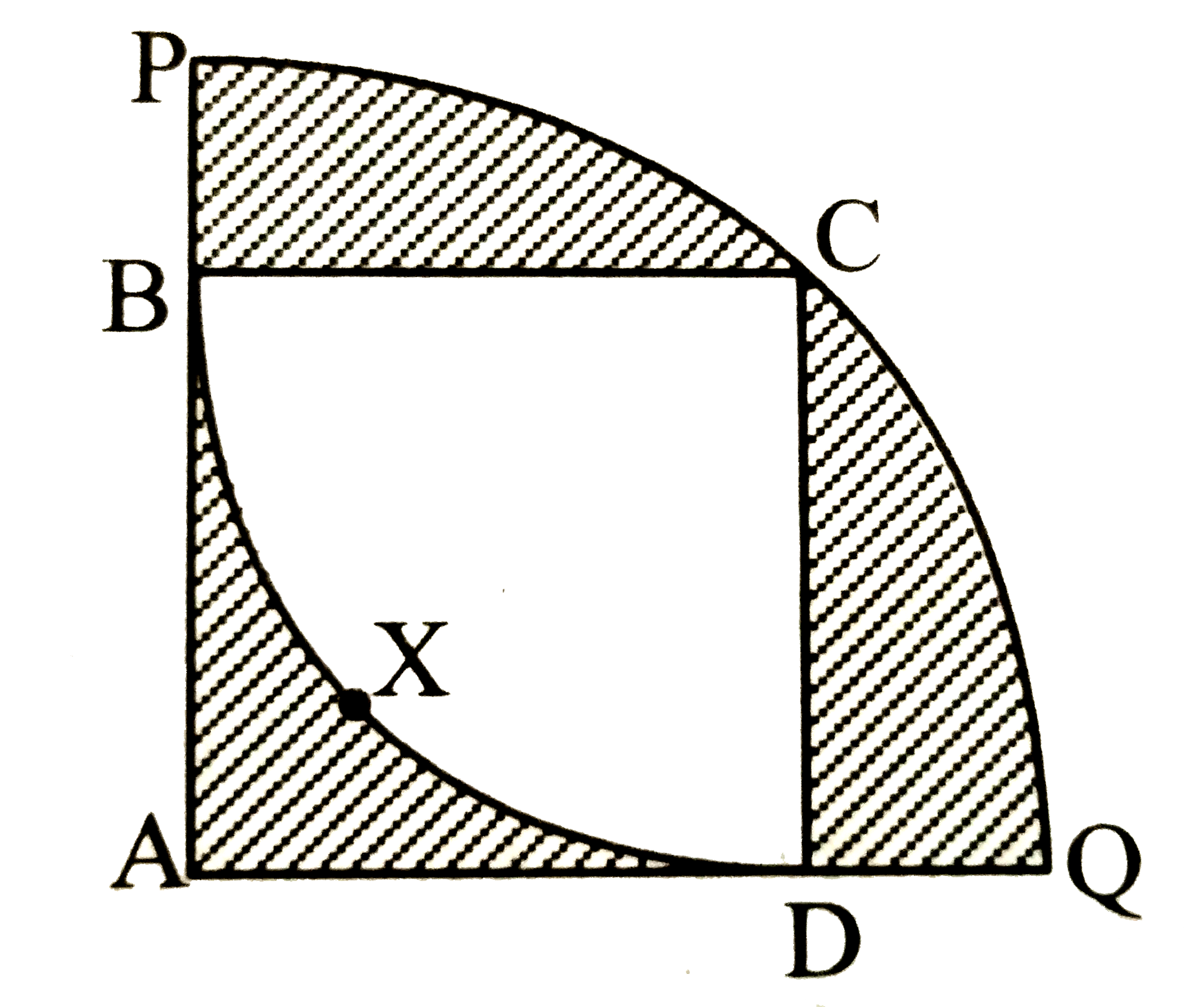 View Solution
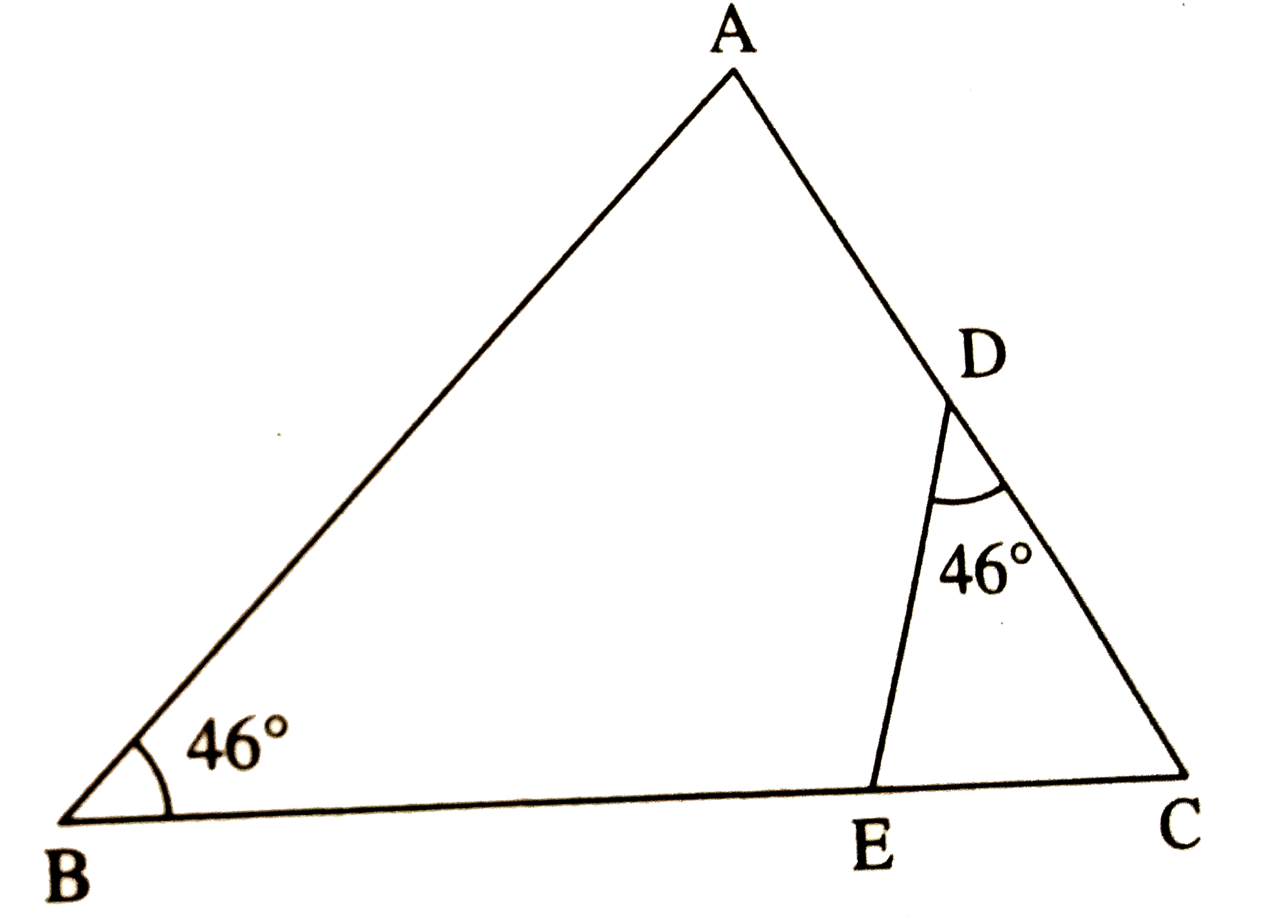
View SolutionIn trapezium PQRS, side PQ∣∣ side SR, AR=5AP, AS=5AQ then prove that SR=5PQ by completing the following activity.
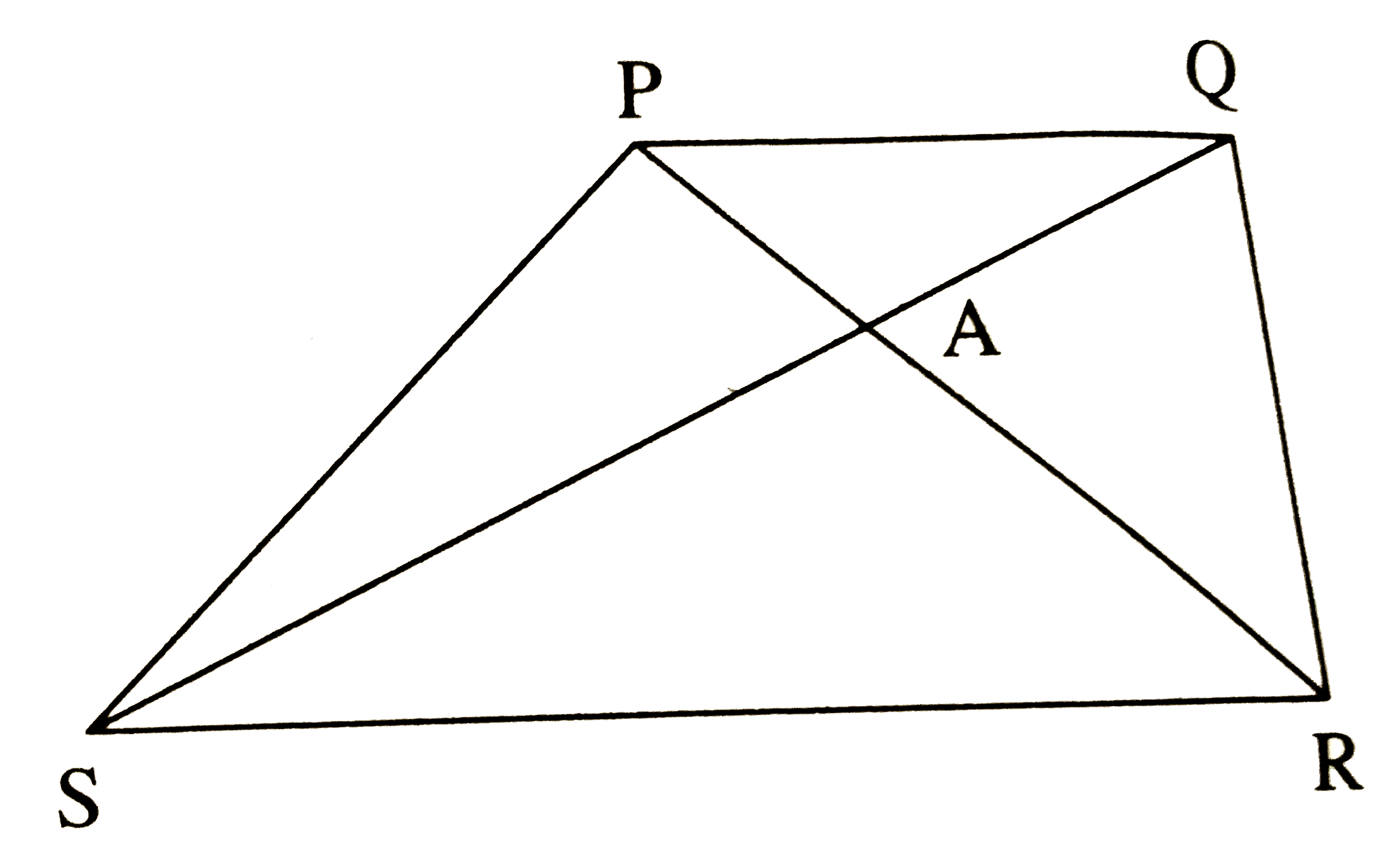
In ΔPQA and ΔRSA,
∠PQA≅∠RSA……(□)
∠PAQ≅∠RAS....(□)
∴ΔPQA~ΔRSA ......(□)
PQSR=□AR.........(Corresponding sides of similar triangles).....(1)
Substituting AR=5AP in (1)
∴PQSR=□5AP
∴PQSR=□5
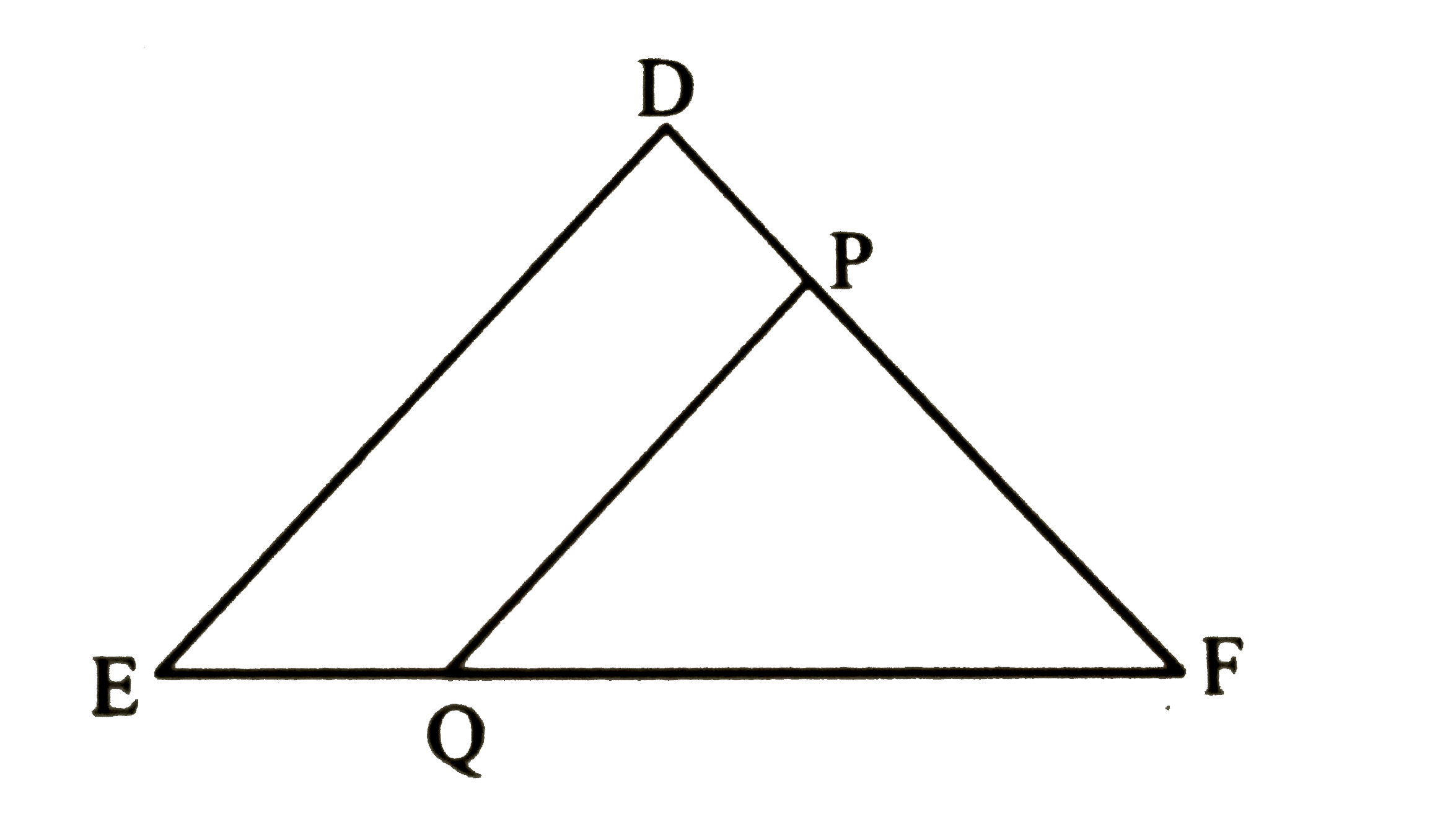
∴SR=5PQView SolutionIn the adjoining figure, seg PQ||seg DE, A(ΔPQF)=20 sq. uints, PF = 2 DP, then find A (□DPQE) by completing the following activity.
 View Solution
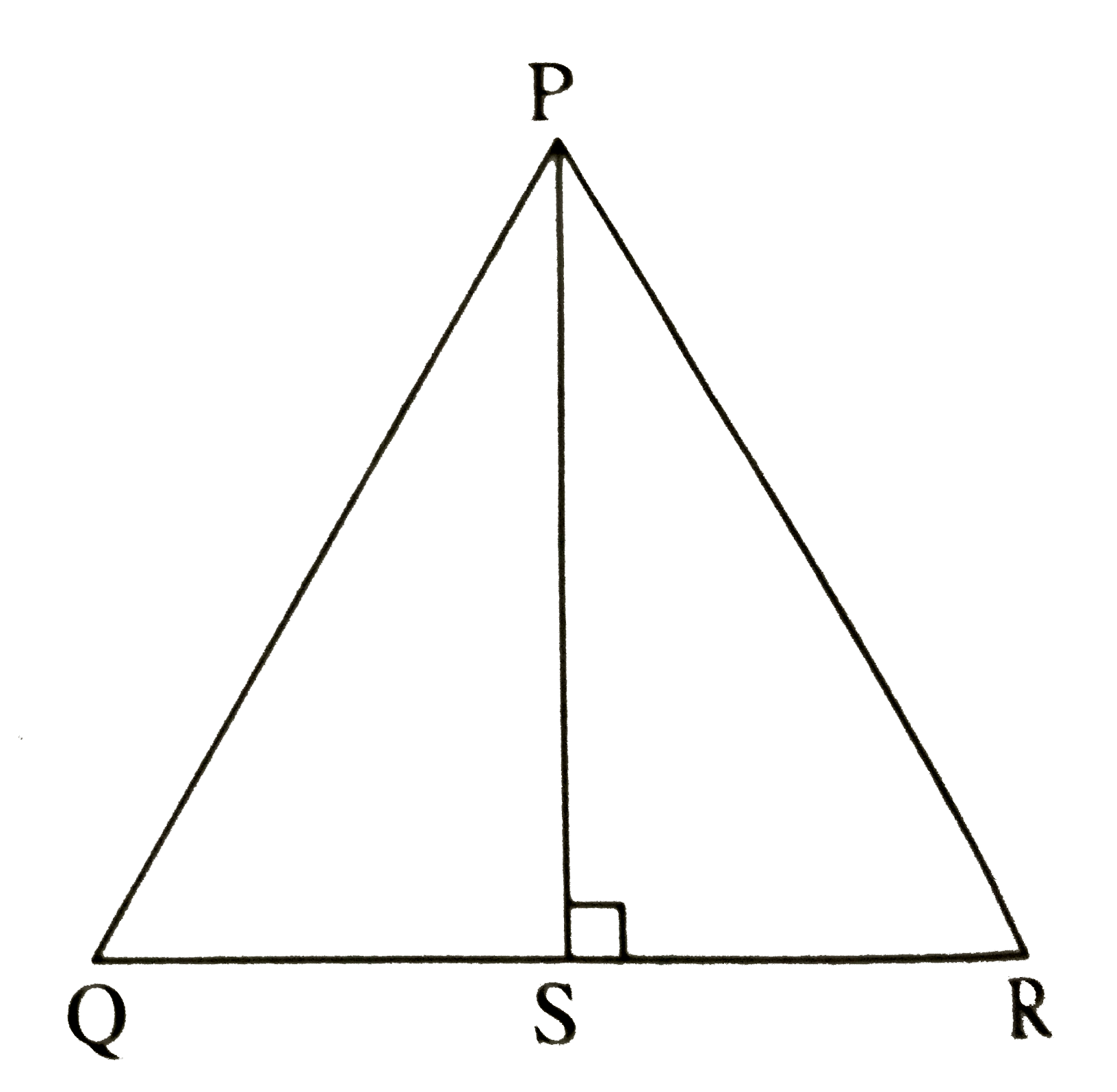
View SolutionΔPQR is an equilateral triangle. Seg PS⊥ side QR such that Q−S−R. Prove PS2=3QS2 by completing the following activity.
In ΔPQS,
∠PSQ=□……(Given)
∠Q=□………….(Angle of an equilateral triangle)
∴∠QPS=30∘.................(Remaining angle of ΔPQS)
∴ΔPQS is a □ triangle
PS=□PQ.............(Side opposite to 60∘)..............(1)
and QS=□PQ..........(Side opposite to 30∘)
PQ=2QS .....(2)
Substituting value of PQ from (2) in (1)
PS=√32×2QS
∴PS=□QS
∴PS2=3QS2......(Square both the sides)
 View Solution
View SolutionIn the figure □ ABCD is a cyclic quadrilateral.Seg AB is a diameter . If ∠ADC=120∘ , complete the following activity to find the measure of ∠BAC.
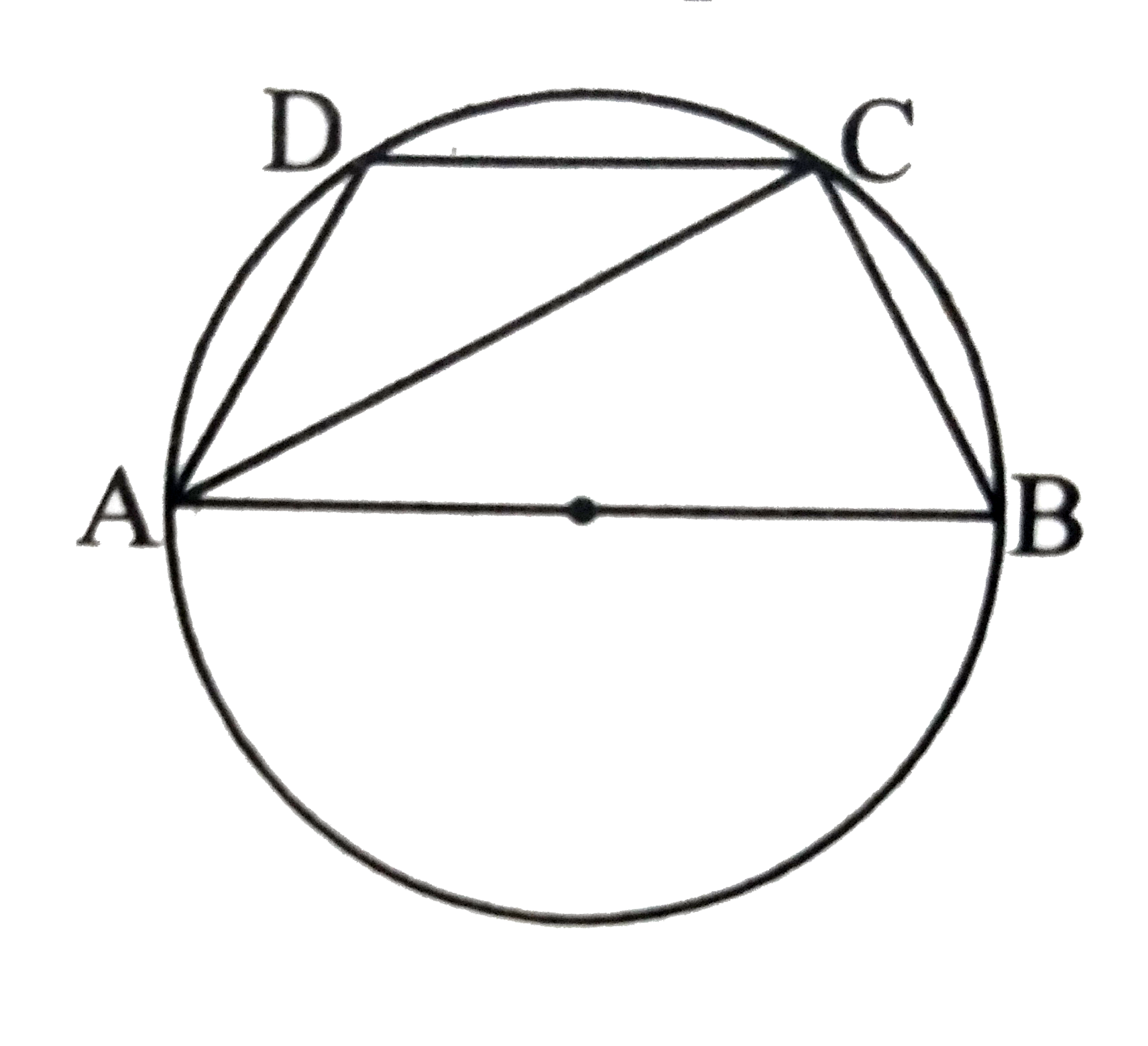 View Solution
View Solution