A circle with centre P is inscribed in the Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
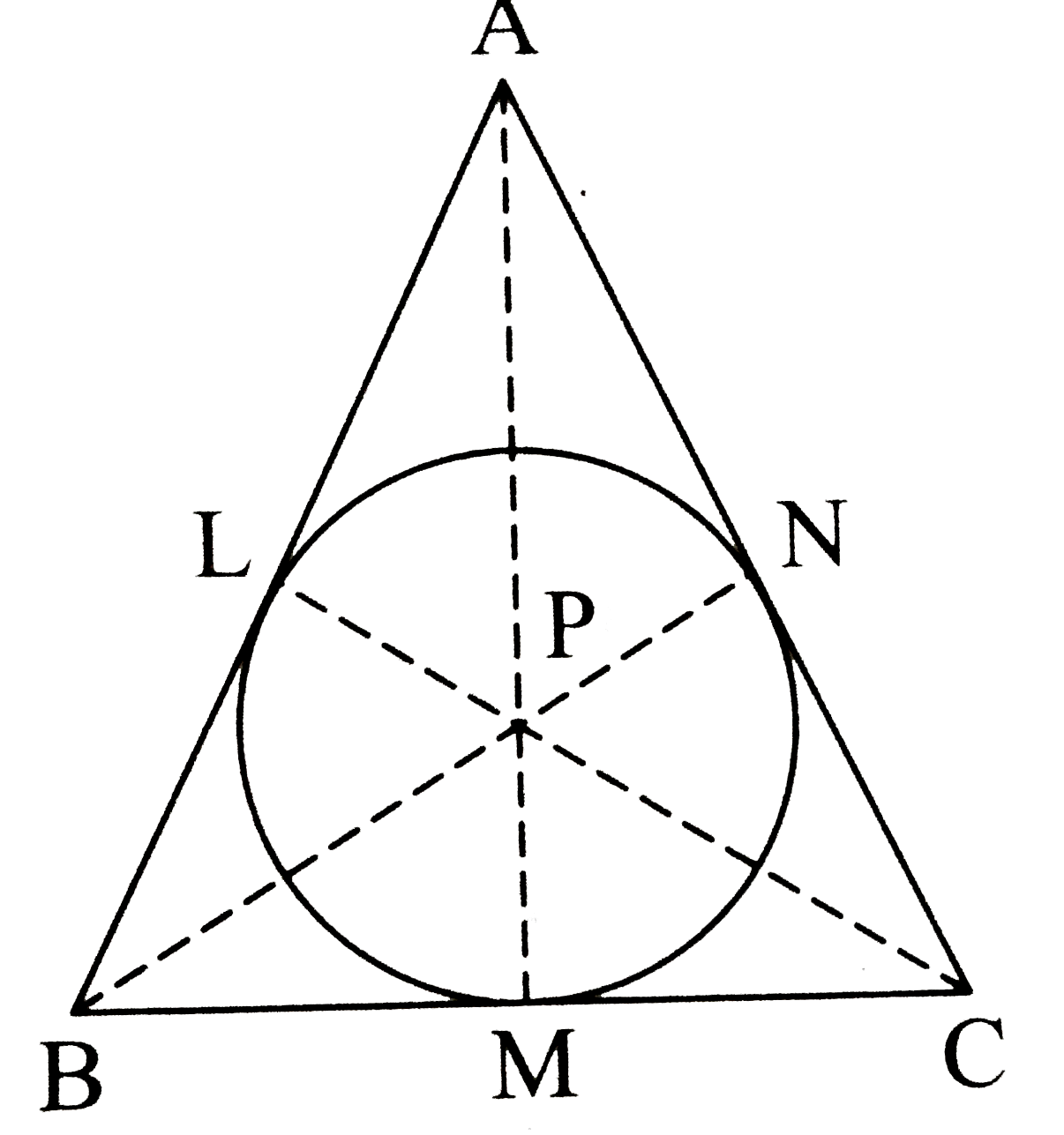
Draw seg PA, seg PL , seg PN , seg PB , seg PC and seg PM
PL = Pm = PN = r …(radii of the same circle)
… (Tangent theorem )
... (1)
Similarly,
...(2)
..... (Area addition postulate )
[ From (1), (2) and (3)]
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE )7videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Choose the correct alternative :3videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE22videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
Similar Questions
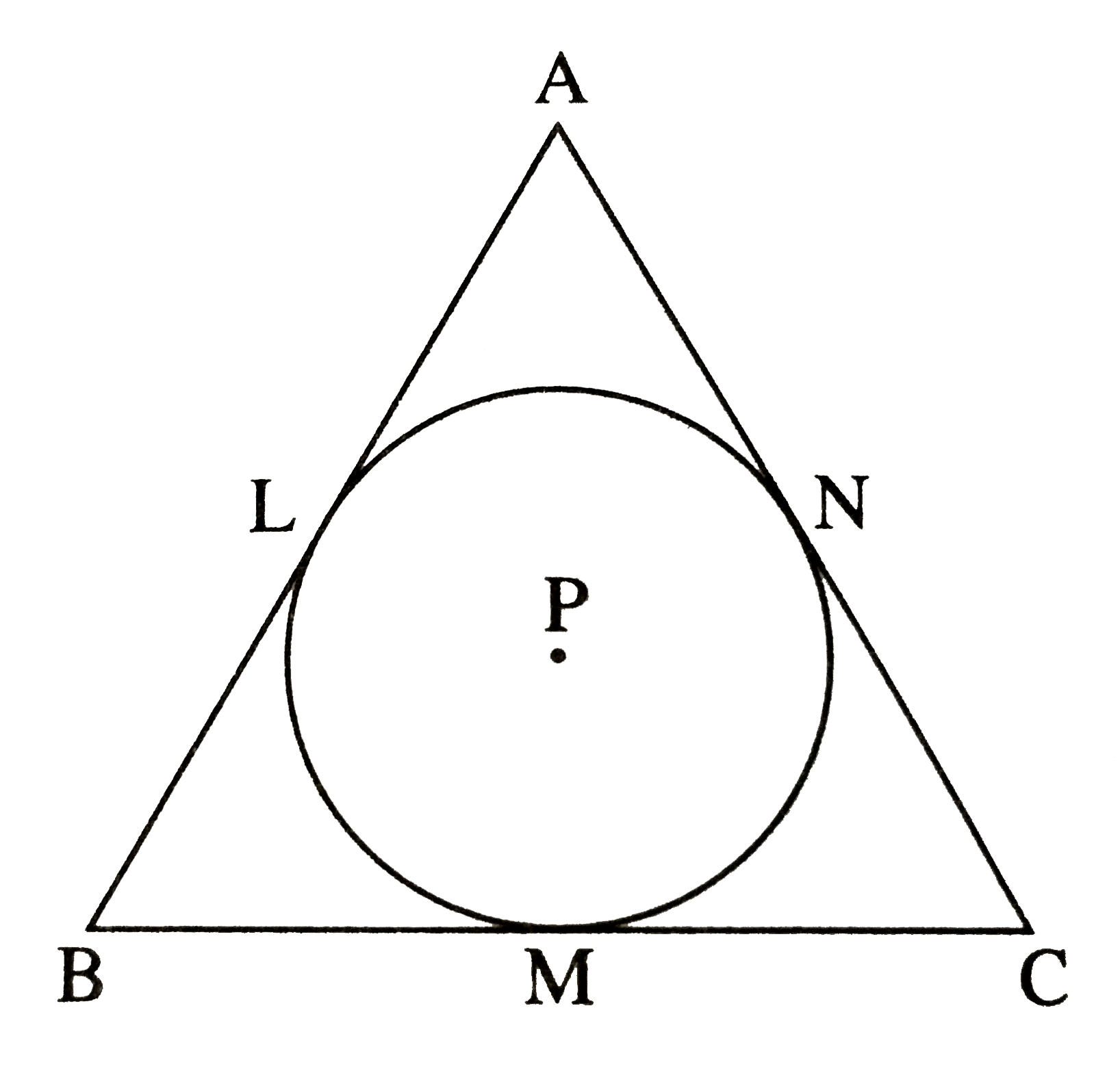
A circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
 View Solution
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View Solution
Knowledge Check
- Question 1 - Select One
In figure , the sides AB, BC and CA of triangle ABC, touch a circle at P,Q and R, respectively . If PA = 4 cm , BP = 3 cm and AC = 11 cm , then length of BC is
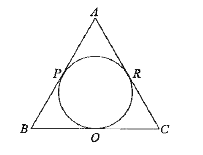 A11 cmB15 cmC14 cmD10 cm
A11 cmB15 cmC14 cmD10 cm - Question 2 - Select One
A circle is inscribed in Δ PQR having sides 8 cm, 10 cm and 12 cm. A circle touches the sides PQ, QR and RP at D, E and F. Find PD
A5 cmB6 cmC4 cmD10 cm
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.
 View Solution
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View SolutionA circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View SolutionA circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively Prove that AQ=12(Perimeter of ΔABC)
View SolutionThe side AB, BC and CA of triangle ABC touch a circle at P,Q and R respectively. If PA =4 cm, BP=3 cm and AC=11 cm, then length of BC is
 View Solution
View SolutionThe incircle of an isosceles triangle ABC, with AB=AC, touches the sides AB, BC, CA at D,E and F respectively. Prove that E bisects BC.
View Solution

