Seg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
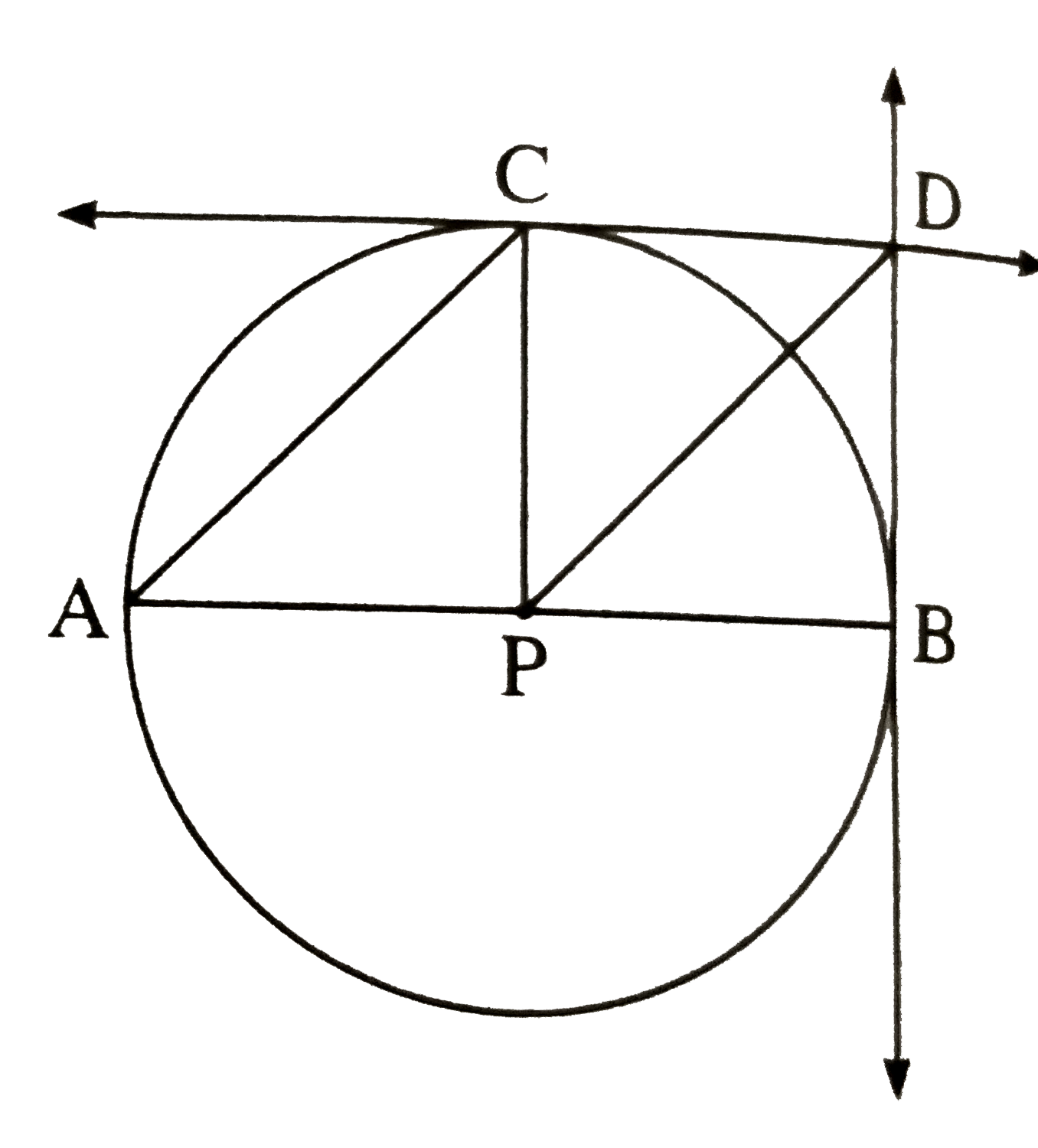
In ΔPAC ,
seg PA≅segPC …(Radii of the same circle )
∴Ang≤PAC≅∠PCA …(Isosceles Delta theorem ) …(1)
seg AC ∣∣ seg PD nd PA is the transversal ,
∠PAC≅∠BPD ...(Corresponding angles ) ... (2)
seg AC ∣∣ seg PD and PC is the transversal ,
∠PCA≅∠CPD ...(ALternate angles ) ...(3)
∴∠BPD≅∠CPD ... [ From (1) , (2) and (3) ] ...(4)
In ΔBPDandΔCPD,
seg BP≅segCP ...(Radii of the same circle )
∠BPD≅∠CPD ...[ From (4)]
seg PD≅segPD ...(Common side )
∴ΔBPD≅ΔCPD (SAS test)
∴∠PBD≅∠PCD ... (c.a.c.t.)
∠PCD=90∘ ... (Tangent is perpendicular to radius )
∴∠PBD=90∘
∴ line DB is tangent to the circle at point B
... ( Converse of tangent theorem )
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE )7videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Choose the correct alternative :3videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE22videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
Similar Questions
In a right Delta, the sum of the squares of sides containing right angle is 225 , then what is the length of its hypotenuse
03:26View Solution(A) Choose the correct alternative :
O is a centre of a circle, Tangents TP and TQ of the circles itersect at point T in the exterior of the circle. Points P and Q lie on the circle . If ∠POQ=120∘ then ∠PTQ=?02:11View SolutionSolve:
(i) 8x+2y+32x−y=3,12x+2y−62x−y=1.
(ii) 2x−1+3y−2=1,5x−1+6y−2=7
(iii) 13x+y+13x−y=1235,12x(3x+y)−12(3x−y)=23502:45View SolutionIn the figure, a semicircle with its diameter on the hypotenuse of a right angled triangle, is shown touching the remaining sides of the triangle. The two parts of the hypotenuse made by the centre of the semicircle have lenghs 15 cm and 20 cm respectively. Find the radius of the semicicle.
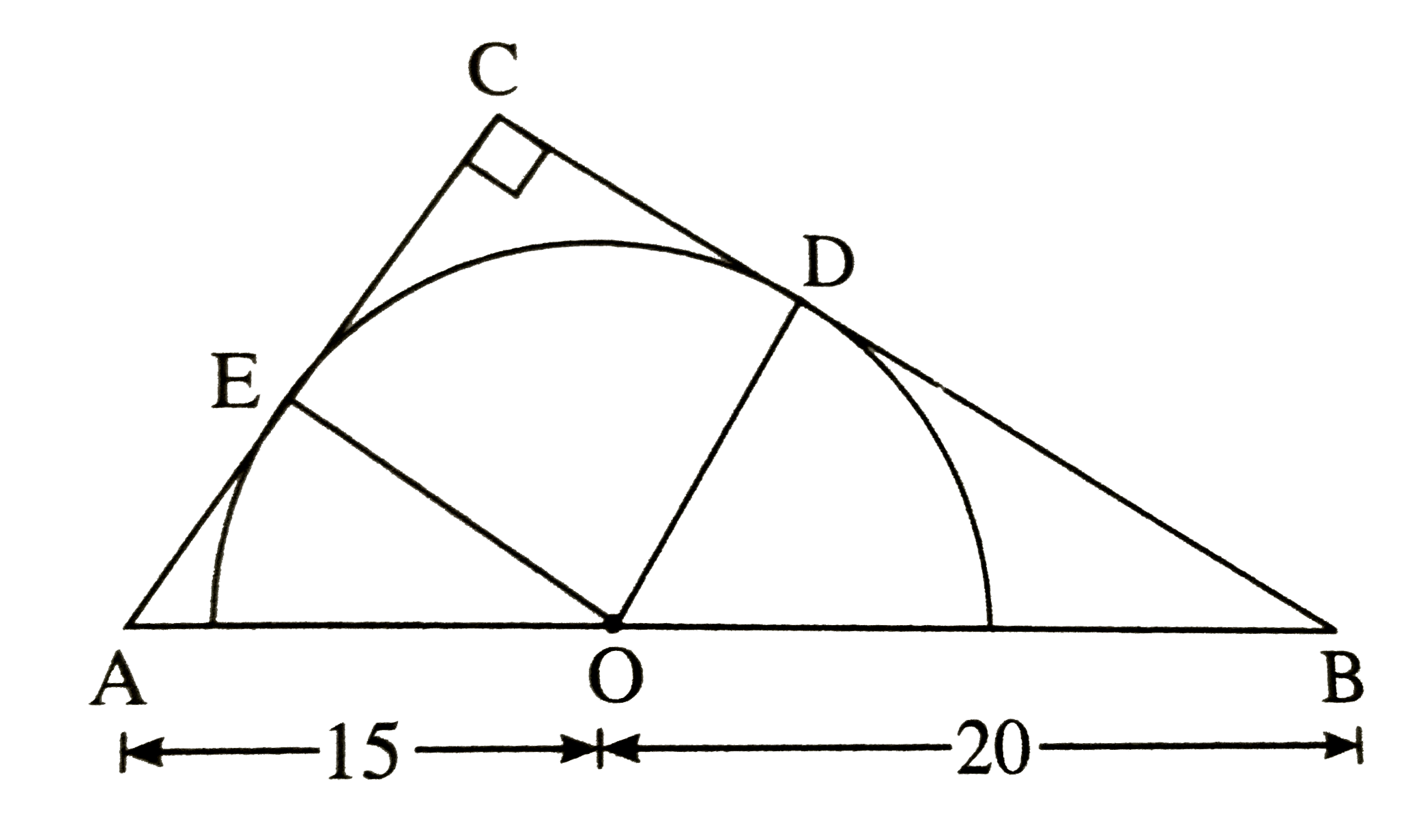 02:17View Solution
02:17View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and AB=CD . If /_MON =120^(@) , then find /_ OPN .
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
04:27View SolutionMatch the following Column A to Column B
 09:54View Solution
09:54View SolutionMatch the following Column A to Column B
 05:01View Solution
05:01View SolutionMatch the following Column A to Column B
 07:34View Solution
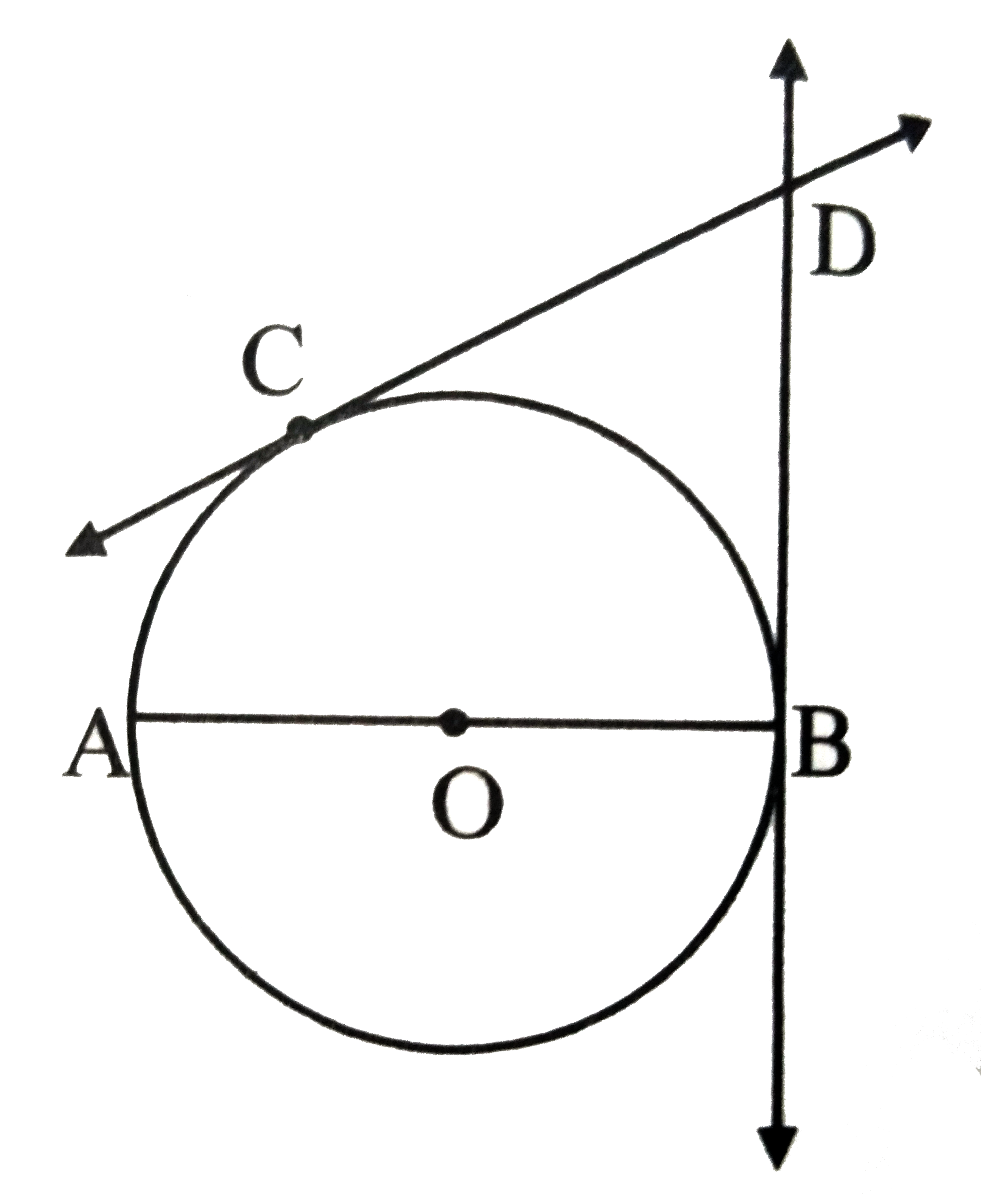
07:34View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
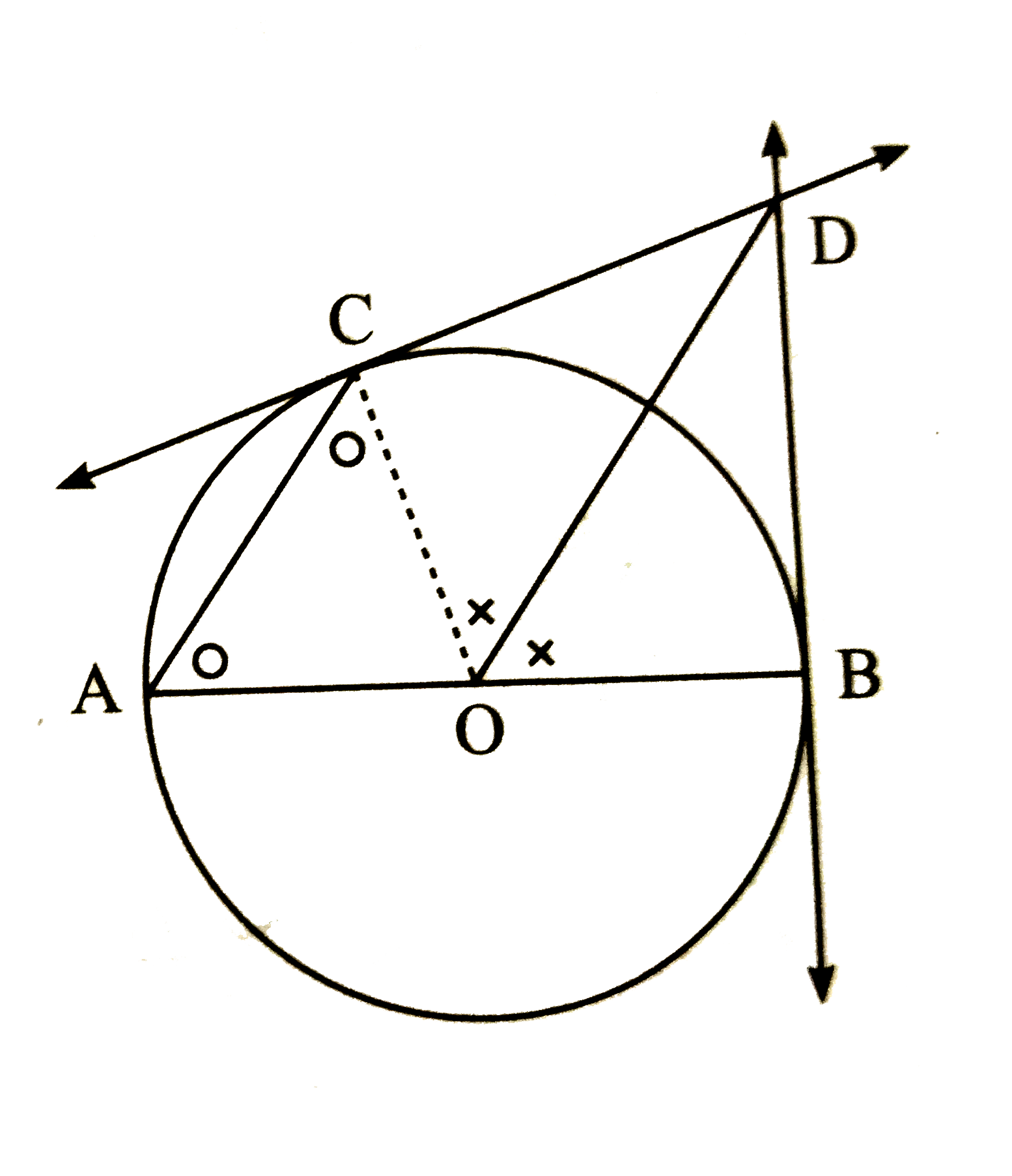 03:00View Solution
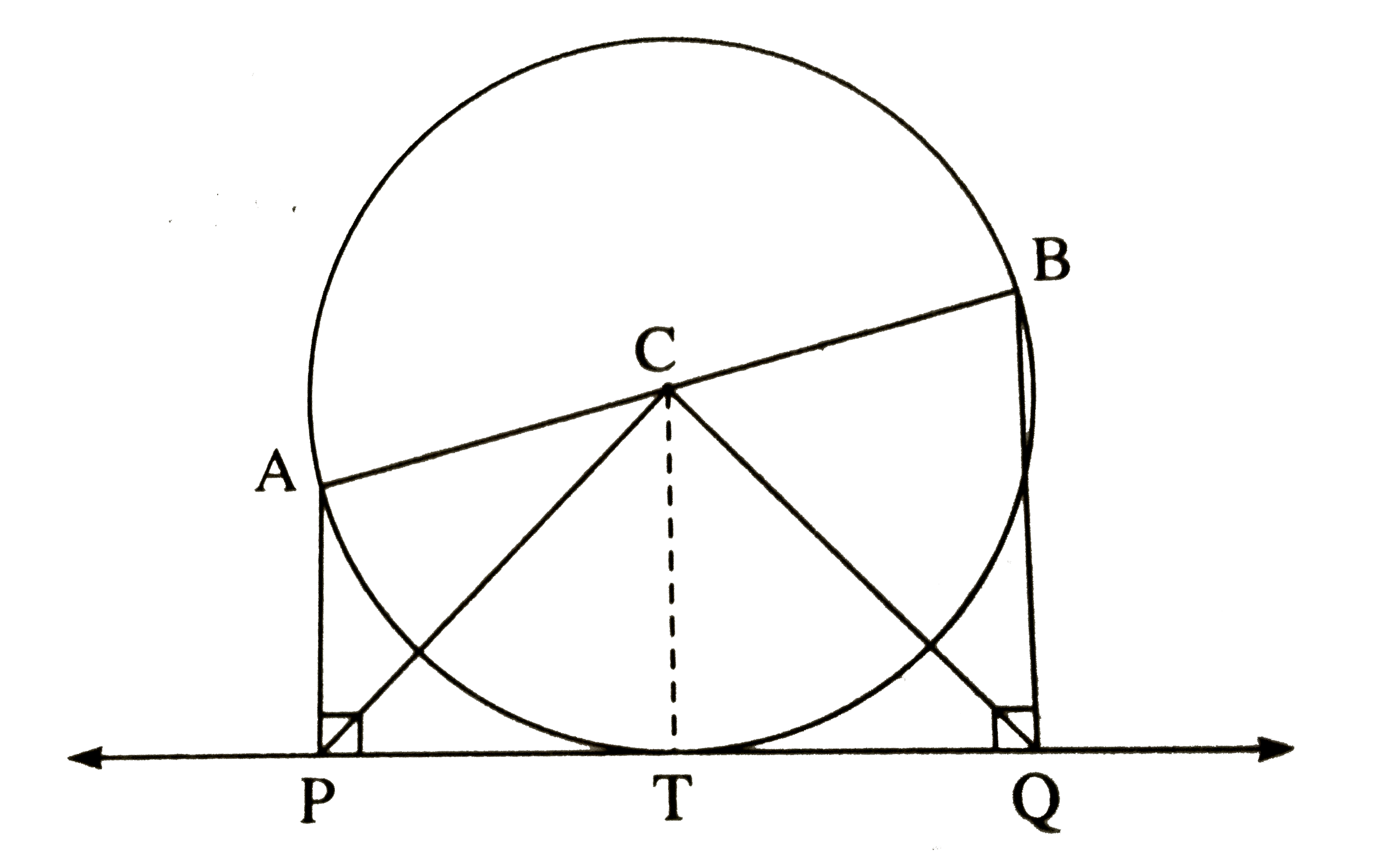
03:00View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.
 09:50View Solution
09:50View SolutionIn the adjoining figure, M is the centre of the circle and seg AB is a diameter. Seg MS⊥ chord AD, seg MT ⊥ chord AC, ∠DAB≅∠CAB.
Prove that : chord AD≅ chord AC.
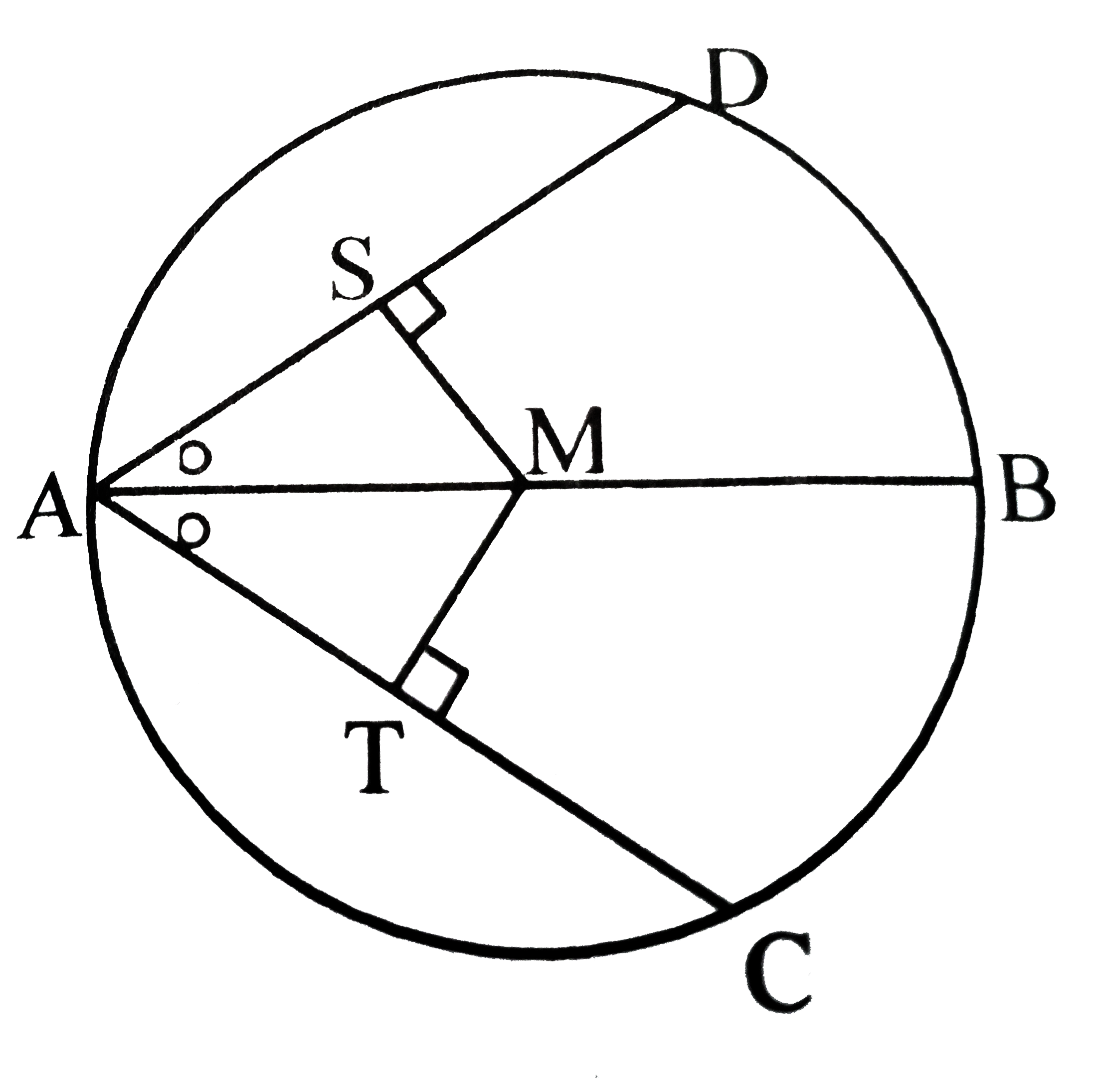 07:09View Solution
07:09View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
 03:16View Solution
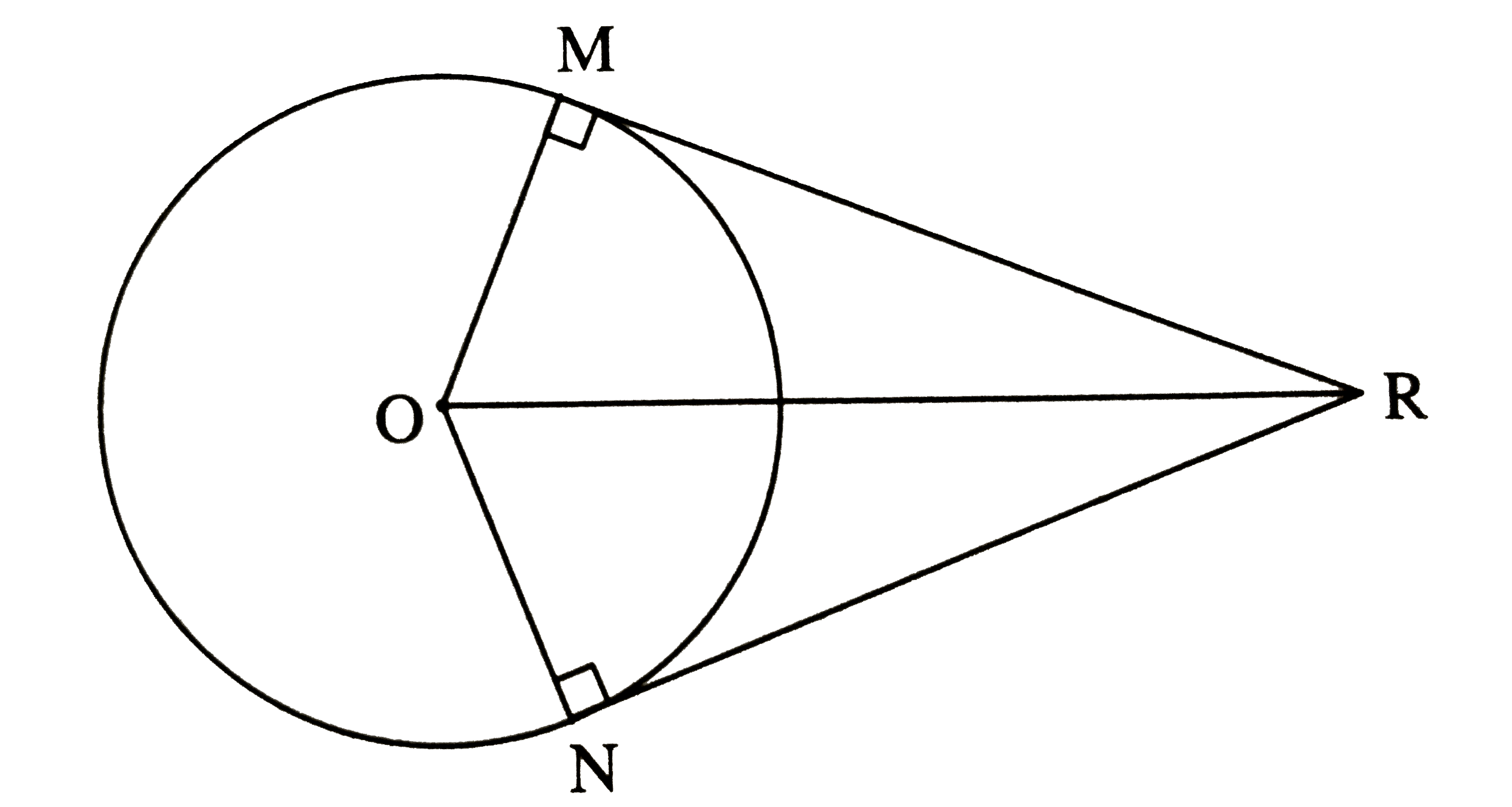
03:16View SolutionSeg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON.
 09:25View Solution
09:25View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
 07:03View Solution
07:03View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
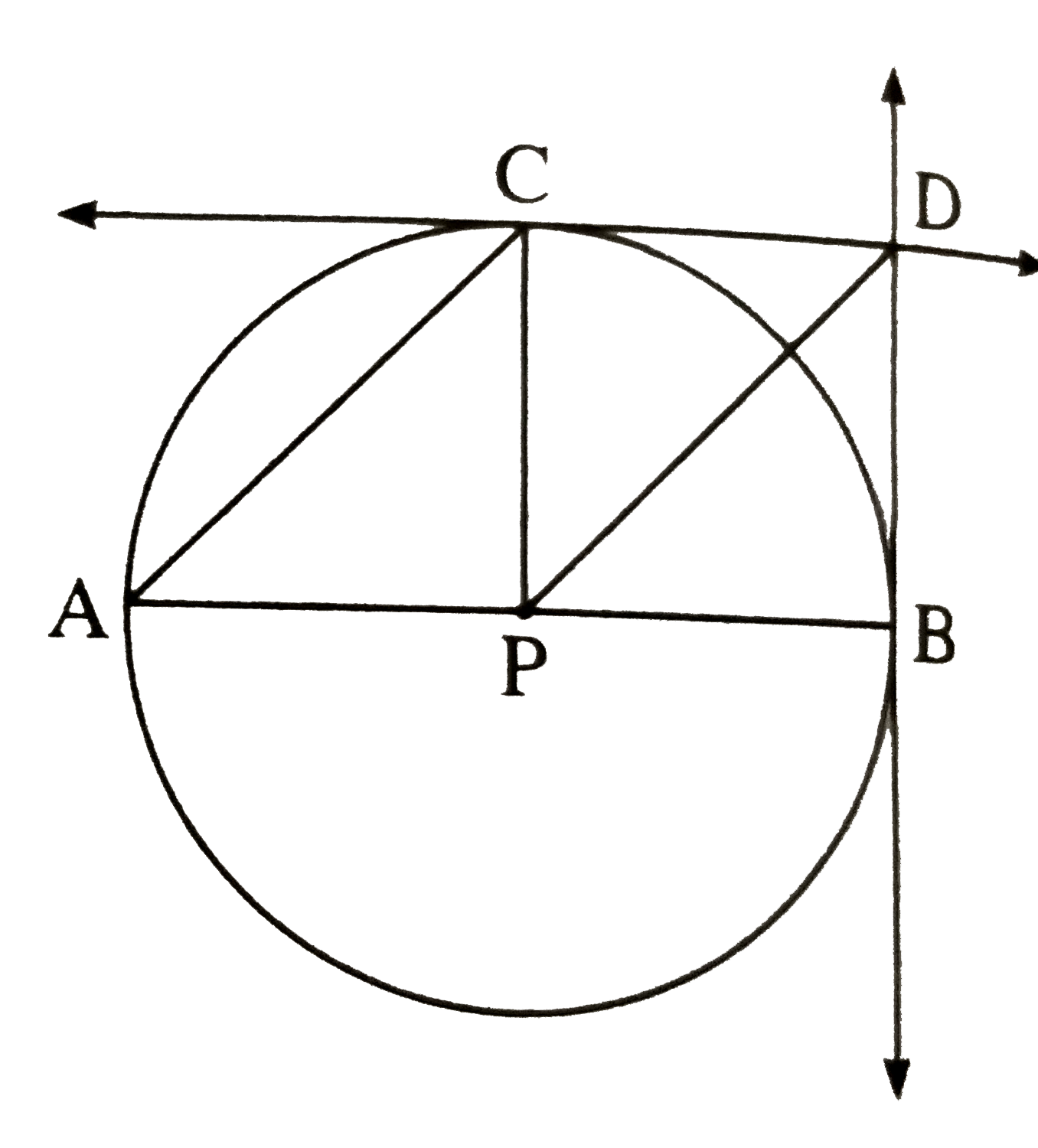 06:11View Solution
06:11View Solution

