(A) Complete any two out of three activites :
(##NVT21_MATP2X_C09E02010_Q01.png width=80%>Inthefigure,segmentsBCandBAaretan≥nts.P∮sCandAarethep∮sCandAarethep∮sofcontact.Oisthecentreofthe∘≤.Comp≤tethefollow∈gactivity→proveseg<br>ODistheperpendica––rbisec→rofsegAC.<br>Pr∞f:<br>OC = OA ... square<br> BC = square ...(Tan≥ntsegmentsdrawnomanexternalp∮→the∘≤areequal.)<br> :. p∮sOandBare square omthep∮sAandCofthechordAC<br> :. byperpendicr–bisec→rtheorem,<br>segOBisthesquareofsegAC<br>i.esegODistheperpendica––rbisec→rofsegAC(O-D_B)
Text Solution
The correct Answer is:radii of the same circle , BA , equidistant , perpendicular bisector
|
Topper's Solved these Questions
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any four of the following subquestions :
4 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Complete any one out of two activities :
2 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve the following subquestions :
3 Videos
- CHALLENGING QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE
22 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
Similar Questions
Knowledge Check
In figure ,PR = ?
(##CEN_JEE_MAT_X_C14_E01_032_Q01.png" width="80%">A20 cmB22 cmC24 cmD26 cmIn the figure shown
(##AHT_PGT_PHY_C10_E01_006_Q01.png" width="80%">AP>P0BP<P0CP=P0DP=0The probability distribution of X is
(# #TRG_MAT_MCQ_XII_P2_C08_E02_005_Q01.png" width="80%">
Then P(X is odd)=A0.45B0.55C0.65D0.75
Observe: the images below.Is it national why ?
(##NVT_SCI_TECH_DIG_X_P2_C09_E13_006_Q01.png" width="80%">
View SolutionSolve any two of the following subquestions :
In the figure , O is the centre of the circles and AP is the tangent to the circle at point A . Ray AF is the bisector of ∠BAC
Prove : seg AP≅ seg PE<br>
View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
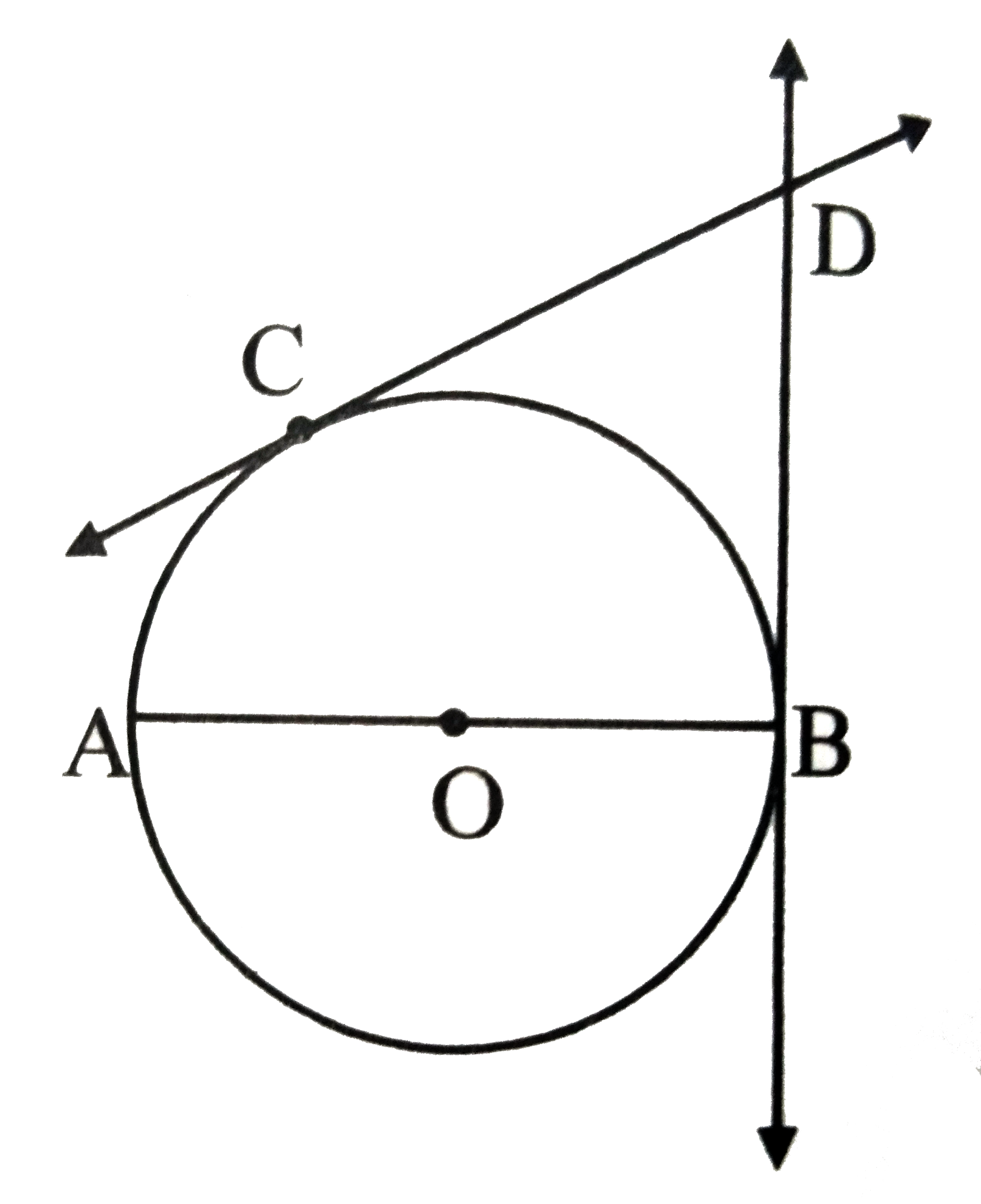
View SolutionSTATEMENT-1:
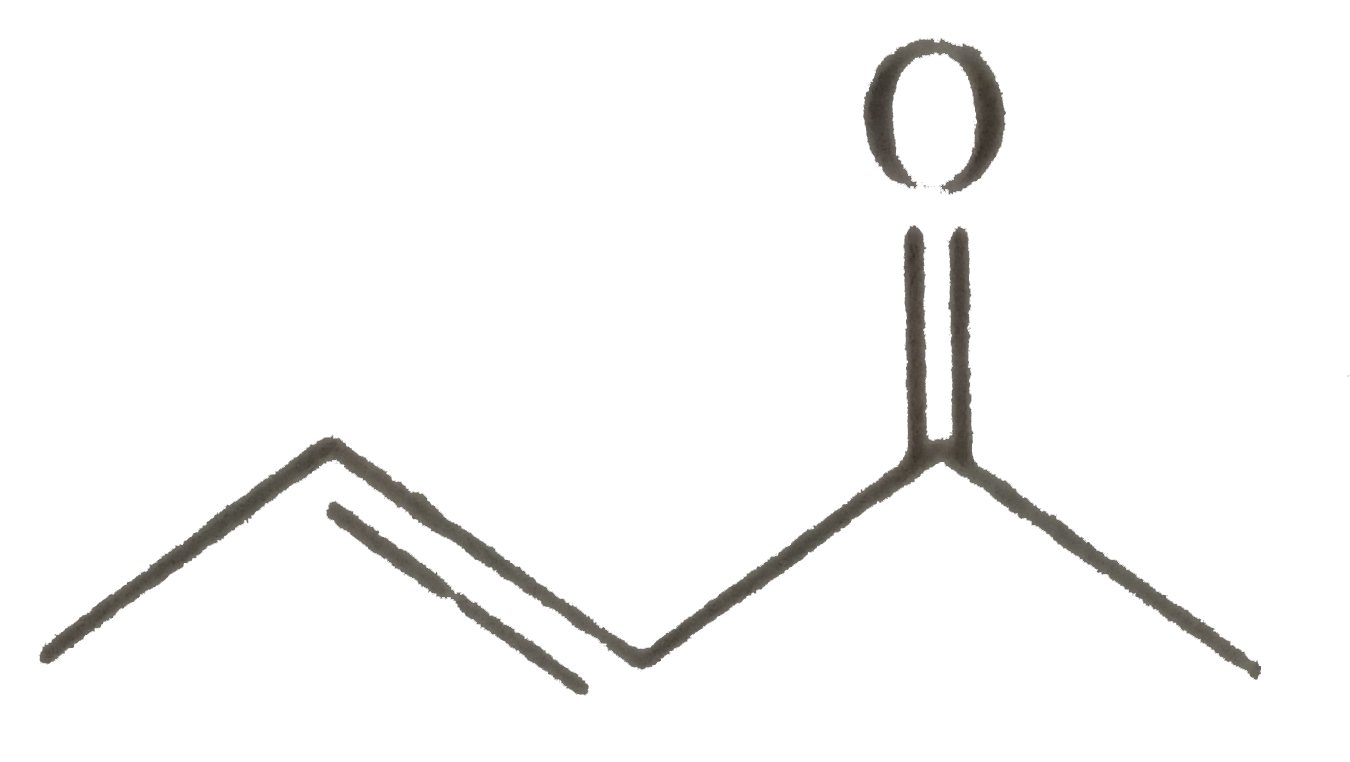
##GRB_ORG_CHM_V02_QB_C03_E01_149_Q02.png" width="80%">
View SolutionThe p.m.f. of a random variable X is
(# TRG_MAT_MCQ_XII_P2_C08_E02_009_Q 01.png" width="80%">
If b= 2a, then
View Solution
