Doubtnut Promotions Sticky

निम्न व्यंजकों के गुणनखंड ज्ञात कीजिए।
(a) y3−7y+6 (b) x3−10x2−53x−42
(c) y3−2y2−29y−42

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(a) माना f(y)=y3−7y+6
स्पष्ट है की f(1)=(1)3−7(1)+6=0
⇒(y−1),f(y) का एक गुणनखंड है।
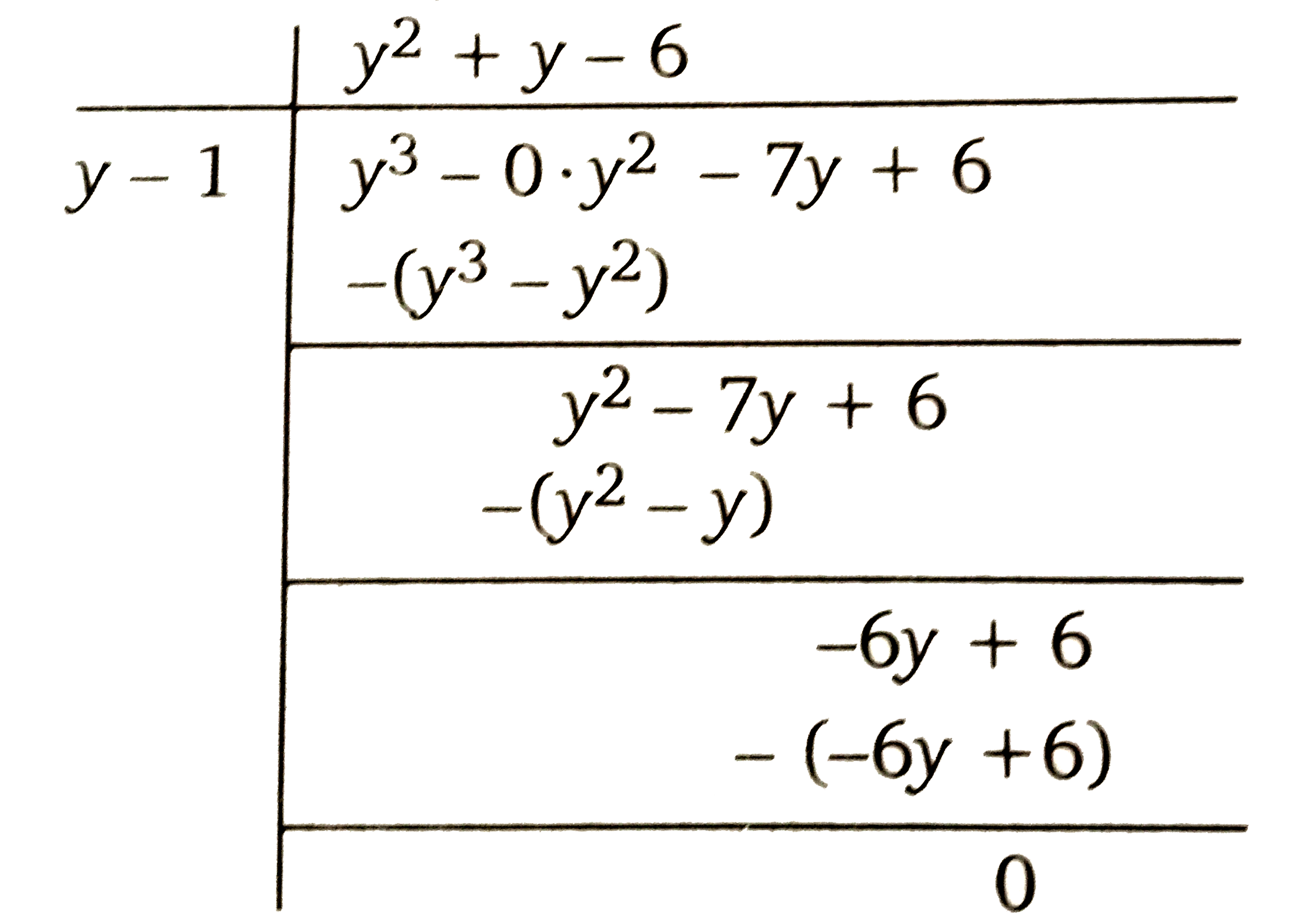
ocr_image
इसलिए f(y)=(y−1)(y2+y−6)=(y−1)(y2+3y−2y−6)
=(y−1)[y(y+3)−2(y+3)]=(y−1)(y+3)(y−2)
(b) माना f(x)=x3−10x2−53x−42
f(x) का अचर पद =−42
अचर पद के गुणनखंड =±1,±2,±3,±6,±7,...±42
अब f(1)=1−10−53−42=−104≠0
f(−1)=(−1)3−10(−1)2−53(−1)−42
=−1−10+53−42=−53+53=0
⇒(x+1), बहुपद f(x) का एक गुणनखंड है।
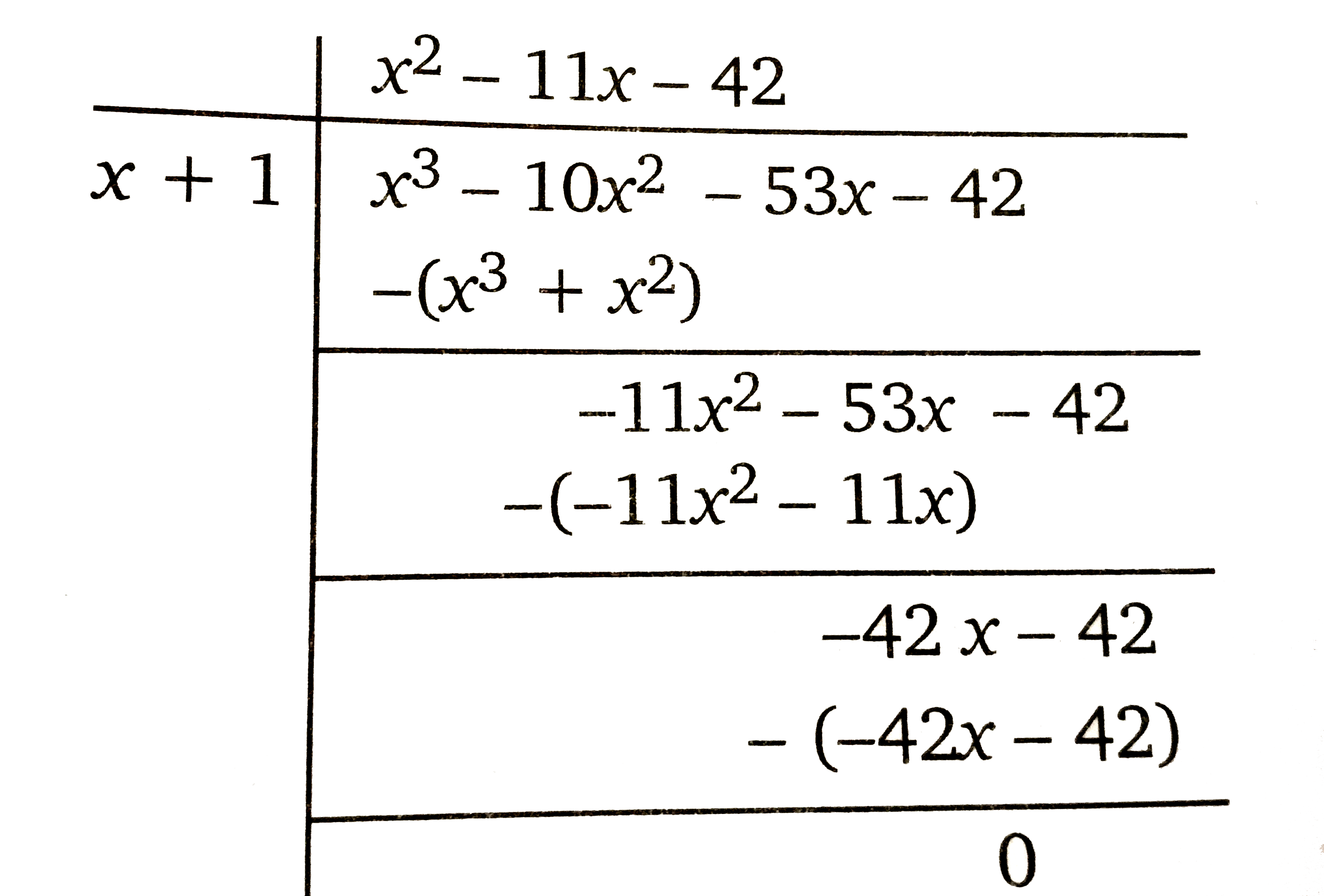
ocr_image
अतः f(x)=(x+1)(x2−11x−42)=(x+1)(x2−14x+3x−42)
=(x+1)[x(x−14)+3(x−14)]=(x+1)(x+3)(x−14)
(c) माना f(y)=y3−2y2−29y−42
f(y) का अचर पद =−42
अचर पद के गुणनखंड =±1,±2,±3,±6,±7,...,±42
अब f(1)=1−2−29−42=−72≠0
f(−1)=(−1)3−2(−1)2−29(−1)−42=−1−2+29−42=−16≠0
f(2)=(2)3−2(2)2−29(2)−42=8−8−58−42=−100≠0
f(−2)=(−2)3−2(−2)2−29(−2)−42=−8−8+58−42=0
⇒(y+2), बहुपद f(y) का एक गुणनखंड है।
ocr_image
अतः f(y)=(y+2)(y2−4y−21)=(y+2)(y2−7y+3y−21)
=(y+2)[y(y−7)+3(y−7)]=(y+2)(y−7)(y+3)

|
Updated on:21/07/2023
Class 9MATHSPOLYNOMIALS

Topper's Solved these Questions

Similar Questions