Question

समीकरण 2y - x = 7 का ग्राफ खीचिए और ज्ञात कीजिए कि बिंदु x = 3, y = 2 समीकरण का हल है अथवा नहीं।

Explanation

यहां दिया गया समीकरण है `2y-x=7`
उपरोक्त की तरह, यहा निम्न तालिका है |

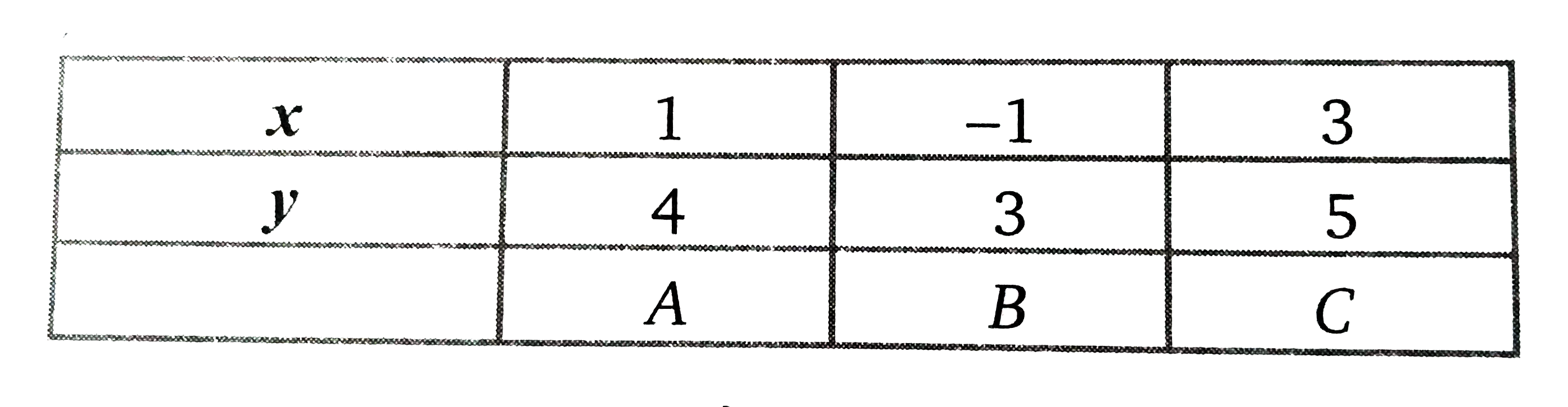
अब बीनउदो `A(1,4), B(-1, 3)` और `C(3,5)` को अंकित करें तथा इन्हे मिला दे तथा हमे एक सरल रेखा प्राप्त होती है |

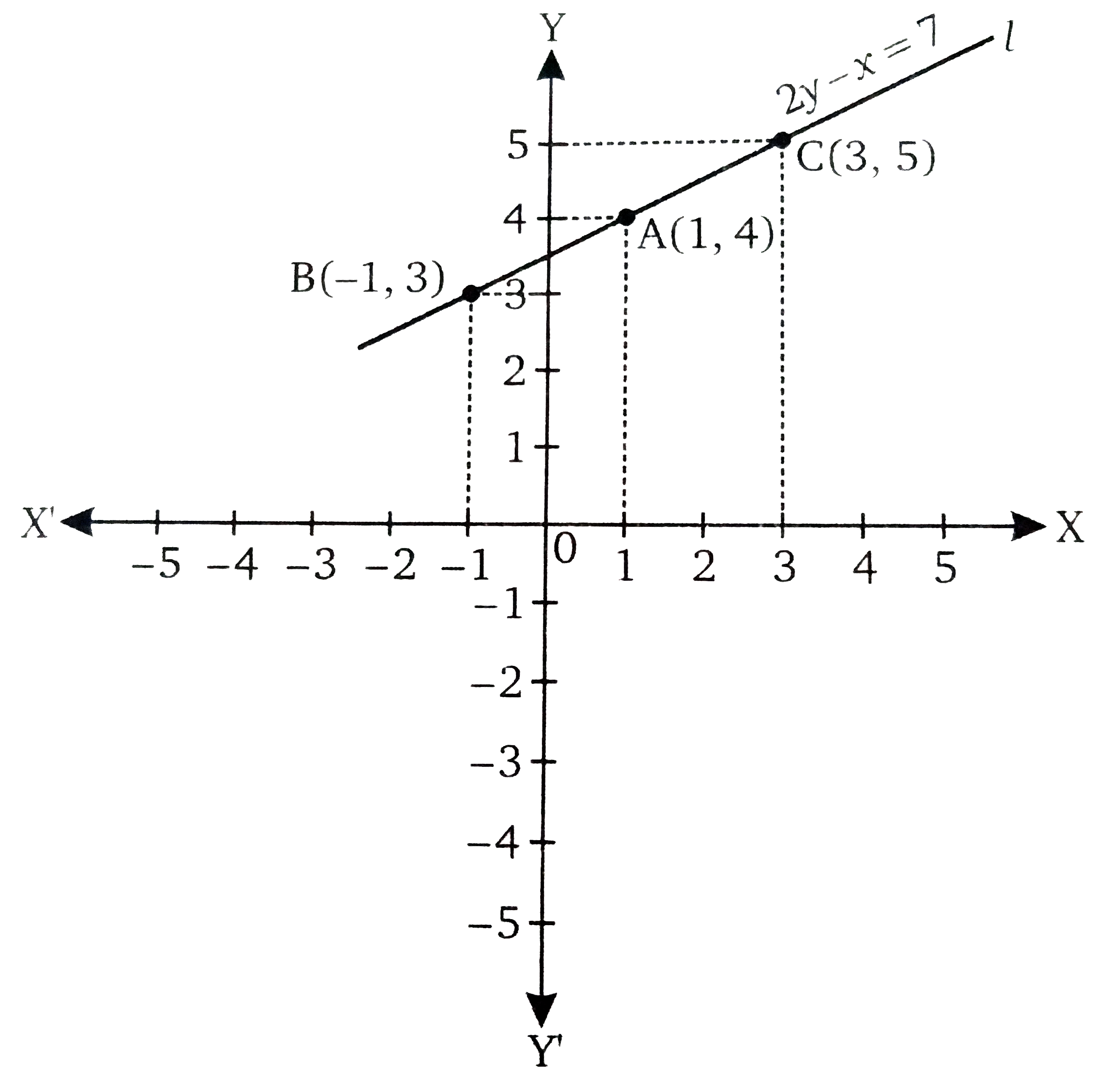
यदि हम बिंदु `(3,2)`को आंकिक करते है तोहम देखते है की बिंदु `(3,2)` समीकरण `2y-x=7` के ग्राफ पर स्थिर नहीं है |
अतः `x=3, y=2` दिए गए समीकरण का एक हल नहीं है |