निम्नलिखित समीकरणों के ग्राफ खिचीय |
4x+3y−7=0
2x−3y+1=
इन ग्राफ में उस बिंदु के निर्देशांक ज्ञात कीजिये, जहां दोनों रेखाएं प्रतिच्छेद करती है
(i) समीकरण 4x+3y−7=0 का ग्राफ
दी गई समीकरण निम्न प्रकार लिखी जा सकती है
y=7−4x3
जब x=−2, y=7−4(−2)3=7+83=5
जब x=4, y=7−4(4)3=7−163=−93=−3
यहां निम्न तालिका है :
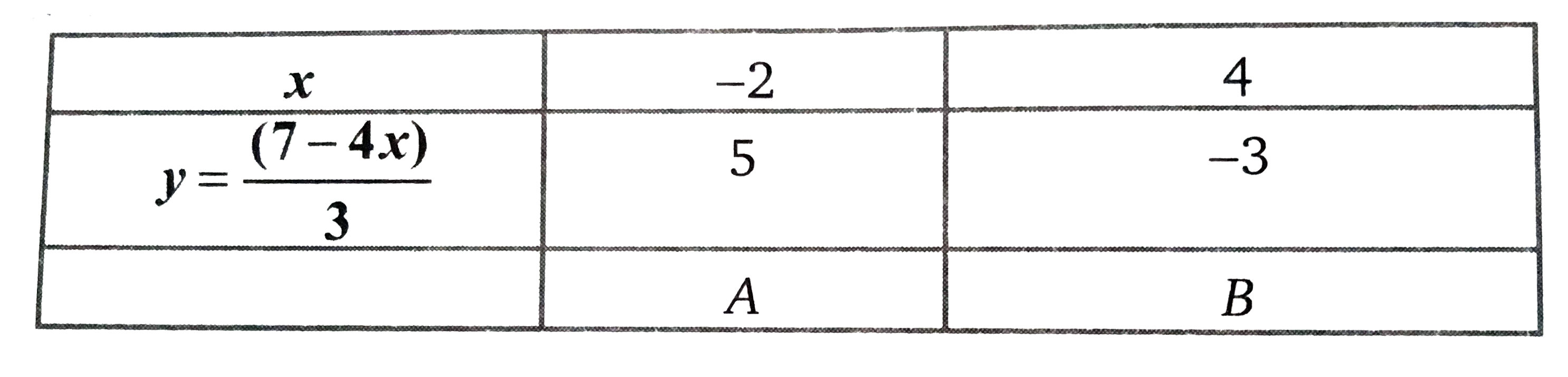
तब, बिन्दुओ A(−2,5) और B(4,−3) को ग्राफ पर अंकित करे तथा इसके तथा इन्हे एक सरल रेखा AB से मिला दे| रेखा AB, समीकरण 4x+3y−7=0 का ग्राफ है |
(ii) समीकरण 2x−3y+1=0
ग्राफ
दी गई समीकरण निम्न प्रकार लिख सकते है |
y=yx+13
जब x=−2,
y=2(−2)+13=−4+13
=−33=−1
जब x=4,
y=2(4)+13
=8+13=93=3
यहां निम्न तालिका है ---

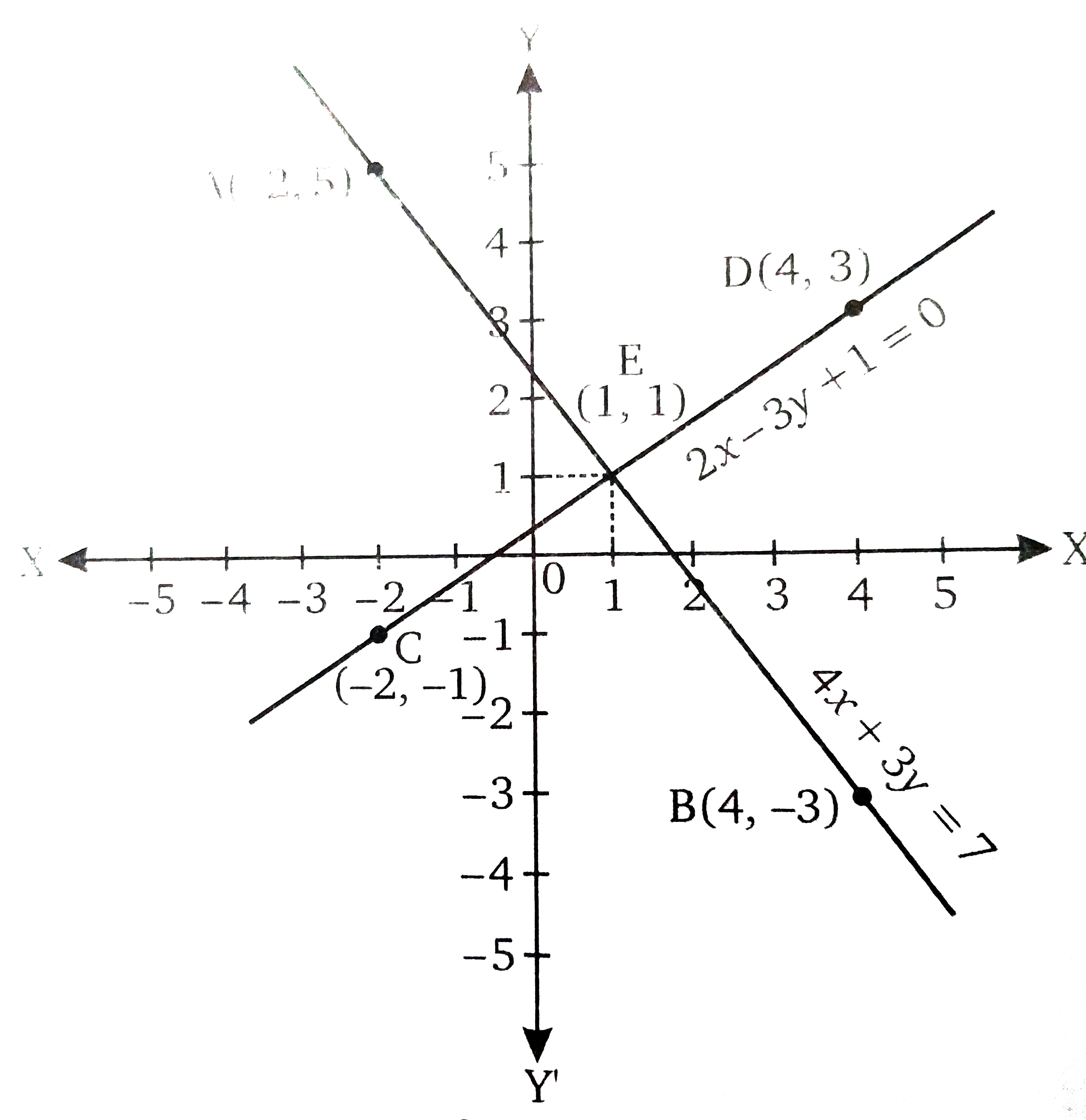
बिंदु C(−2,−1) तथा D(4,3) को ग्राफ पर अंकित करे और अब इन्हे एक सरल रेखा CD द्वारा मिला दे | रेखा CD, समीकरण 2x−3y+1=0 का ग्राफ है |
ग्राफ से हम देखते है की दोनों रेखाएं एक बिंदु E(1,1) पर प्रतिच्छेद करती है |
Topper's Solved these Questions
- दो चरो के रैखिक समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - दो चरो के रैखिक समीकरण EXERCISE - अभ्यास प्रश्न 7.1
30 Videos
- दो चरो के रैखिक समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - दो चरो के रैखिक समीकरण EXERCISE - स्वमूल्यांकन परीक्षण
18 Videos
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - स्वमूल्यांकन परीक्षण
10 Videos
Similar Questions
एक समीकरण का ग्राफ खीचिए यदि,
(i) x=0,y=4 समीकरण का एक हल है |
(ii) x=1,y=5 समीकरण का एक हल है|
(iii) (−4,−4) संकरण के ग्राफ पर स्थिर है |
(iv) रेखा (y−2x=4) और अक्षों के निर्देशांक के द्वारा निर्मित त्रिभुज का क्षेत्रफल
View Solutionएक पुस्तक का मूल्य, एक पैन के मूल्य से दो गुना है | इसे व्यक्त करने के लिए दो चरो का रैखिक समीकरण लिखिये |
View Solutionरेखा l कोण A की समद्विभाजक है तथा l पर कोई बिंदु B है| BP और BQ बिंदु B से ∠Aकी भुजाओं पर लम्ब है तो दिखाइये कि-

(i) ΔAPB≅ΔAQB
(ii) BP=BQ
View Solutionनिम्न बिंदुओं को ग्राफ पेपर पर अंकित करें ।
(i) (3,5) (ii)(−3,4) (iii)(−3,−4)
View Solutionरेखा 4x+3y=12 अक्षो को बिन्दुओ L और M पर प्रतिच्छेद करती है बिंदु इस प्रकार गति करता है की त्रिभुज PLM का क्षेत्रफल सदैव वर्ग इकाई रहता है , तो P का बिन्दुपथ ज्ञात कीजिये
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए , जो रेखाओ x+y=3 तथा 2x+3y=7 के प्रतिच्छेद बिंदु को रेखाओ 2x+3y=8 तथा 3x−y=1 के प्रतिच्छेद बिंदु से मिलती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखा 7x−5y+14=0 के समान्तर है तथा रेखाओ 2x+3y+7=0 और 3x−4y−15=0 के प्रतिच्छेद बिंदु से होकर जाती है ।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionसिद्ध कीजिए कि मूलबिंदु को एक उचित बिंदु(-1,-1) पर स्थान्तरित करके समीकरणों x+3y+4=0 और x−3y−2=0 को x+3y=0 तथा x−3y=0 के रूप में लिखा जा सकता है
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरण निम्न है
4x+3y=27,x−6y=0 तथा 5x−3y=0
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionउस बिंदु के निर्देशांक ज्ञात कीजिए जहां बिंदुओं (5 ,1 ,7 ) और ( 3 ,4 ,1 ) को मिलाने वाली रेखा समतल 4x- 3y -z+ 1=0 को काटती है|
View Solutionदर्शाइए के सरज रेखाएं
¯r=¯i+¯j−¯k+λ(3¯i−¯j) और ¯r=4¯i−¯k+μ(2¯i+3¯k) प्रतिच्छेदी करती है। प्रतिच्छेद बिंदु भी ज्ञात कीजिए।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए जिसके निर्देशांक निम्नलिखित समीकरणों से दिए जाते है :
x=acosϕ,y=bsinϕ, जहाँ ϕ चर है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए जिसके निर्देशांक निम्नलिखित समीकरणों से दिए जाते है :
x=at2,y=2at, जहाँ t चर है ।
View Solutionअन्तराल ज्ञात कीजिये जिनमे से निम्लिखित फलन वर्धमान है या हसयमन है। >br>f(x)=x4−2x2
View Solution
