चित्र में l∣∣m तथा M, रेखाखण्ड AB का मध्य बिंदु है । सिद्ध कीजिए कि M, एक रेखाखण्ड CD, जिसके अन्तः बिंदु l व mपर स्थित है , का भी मध्य बिंदु है ।
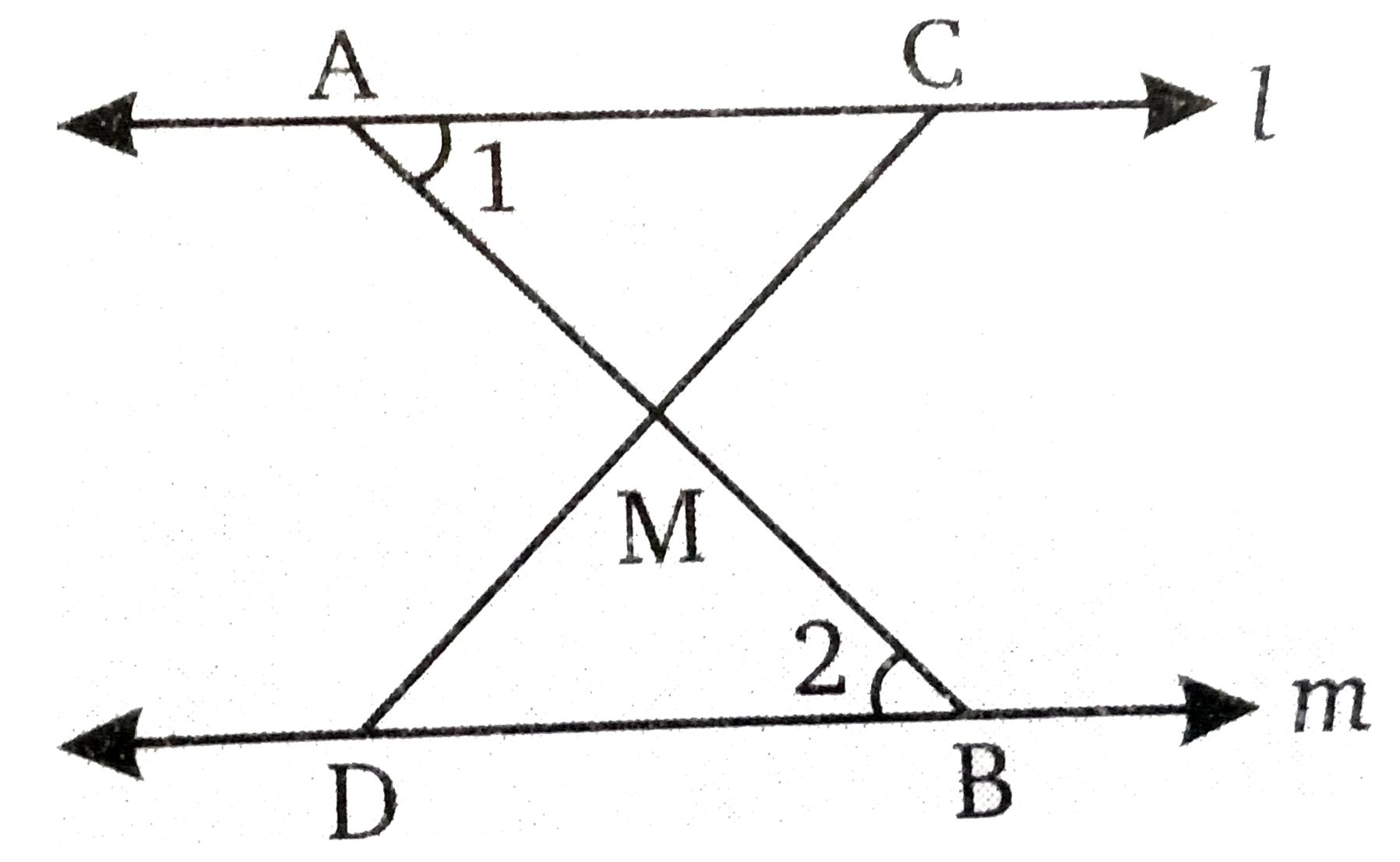
दिया है :l∣∣m तथा M,रेखाखण्ड AB का मध्य बिंदु है । C,l पर कोई बिंदु है तथा D,m पर कोई बिंदु है ।
सिद्ध करना है :M रेखाखण्ड CD का मध्य बिंदु है ।
उपपत्ति : चूँकि l∣∣m तथा AB एक तिर्यक है ।
∴ ∠1=∠2
ΔACM तथा ΔDBMमें ,∠1=∠2 (उपरोक्त से )
AM = MB (दिया है )
∠AMC=∠BMD (शीर्षाभिमुख कोण )
∴ΔACM≅ΔDBM (ASAनियम द्वारा )
∴MC=MD
अतः M रेखाखण्ड CD का मध्य बिंदु है ।
Topper's Solved these Questions
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास प्रश्न 12.111videos
त्रिभुजों की सर्वांगसमता
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास प्रश्न 12.24videos
त्रिभुजों की सर्वांगसमता
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)13videos
त्रिभुज एवं उसके गुण
- BOOK - BALAJI PUBLICATIONCHAPTER - दो चरो के रैखिक समीकरण EXERCISE - स्वमूल्यांकन परीक्षण18videos
दो चरो के रैखिक समीकरण
Similar Questions
चित्र में वर्ग ABCD में एक बिंदु X है । AX पर एक वर्ग AXYZ बनाया जाता है ।
सिद्ध कीजिए किBX = DZ
 02:11View Solution
02:11View Solutionदिये गये चित्र में यदि ∠X=∠Y तथाAB=CB तब सिद्ध कीजिए कि AE = CD
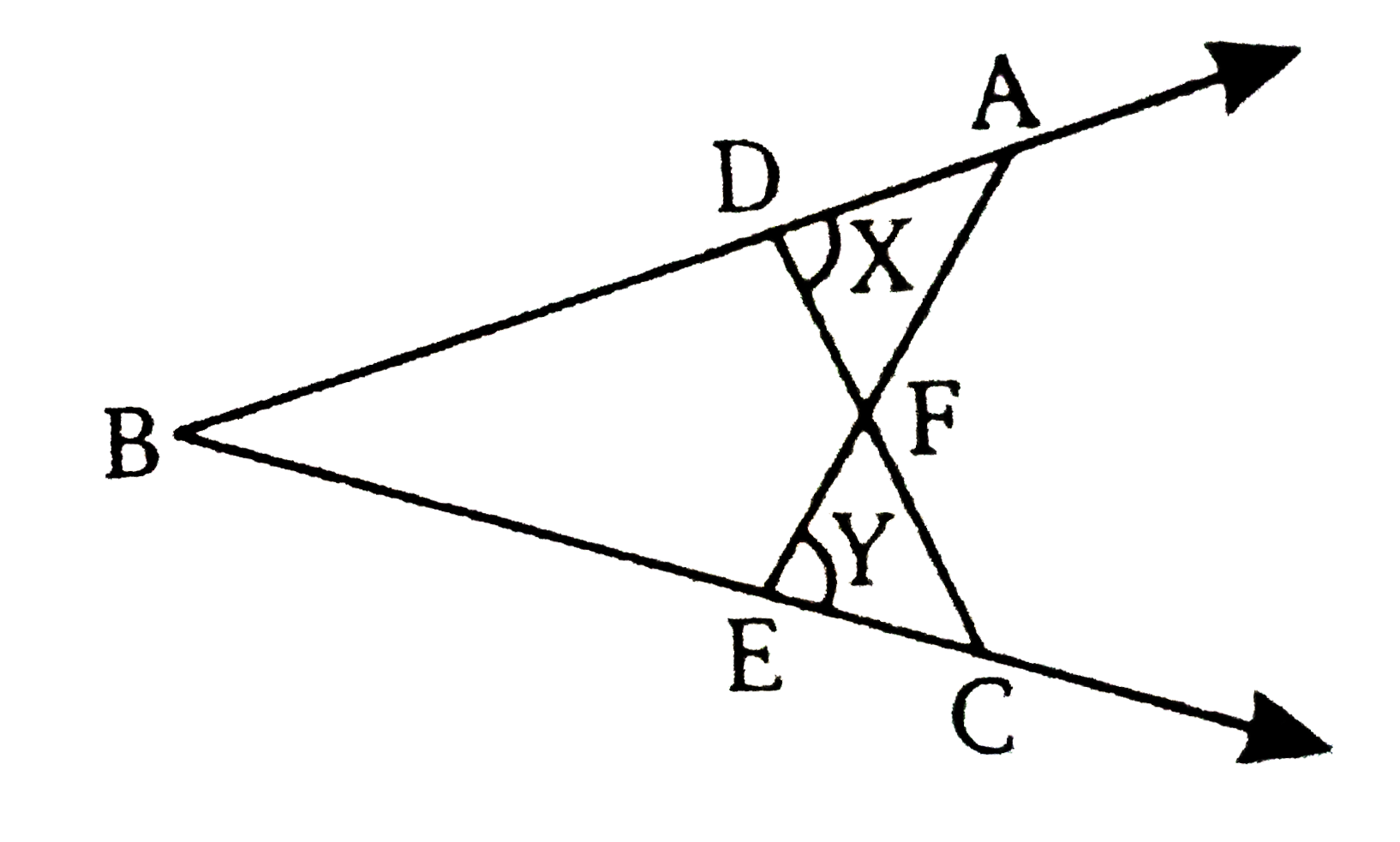 02:45View Solution
02:45View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
02:17View Solutionएक पुस्तक का मूल्य, एक पैन के मूल्य से दो गुना है | इसे व्यक्त करने के लिए दो चरो का रैखिक समीकरण लिखिये |
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 04:29View Solution
04:29View SolutionThe inequation represented by the graph given below is :
03:29View SolutionThe inequation that best describes the graph given below is _________
04:45View SolutionThe inequation that best describes the following graph is _________
05:16View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
03:38View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
05:41View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
05:40View Solutionउस बिंदु P का बिन्दुपथ ज्ञात कीजिए जो इस प्रकार गमन करता है कि बिंदु A(am,0),m≠1 से उसकी दूरी , बिंदु B(am,0) से उसकी दूरी की m गुनी रहती है ।
02:07View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
02:28View Solution
