एक समद्विबाहु त्रिभुज है जिसमें , और इसकी दो माध्यिकाएँ है तो सिद्ध कीजिए कि
Step by step video & image solution for एक समद्विबाहु त्रिभुज ABC है जिसमें AB=AC, BE और CF इसकी दो माध्यिकाएँ है तो सिद्ध कीजिए कि BE = CF by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - बहुविकल्पीय प्रश्न
4 Videos
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास प्रश्न 12.4
8 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)
13 Videos
- दो चरो के रैखिक समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - दो चरो के रैखिक समीकरण EXERCISE - स्वमूल्यांकन परीक्षण
18 Videos
Similar Questions
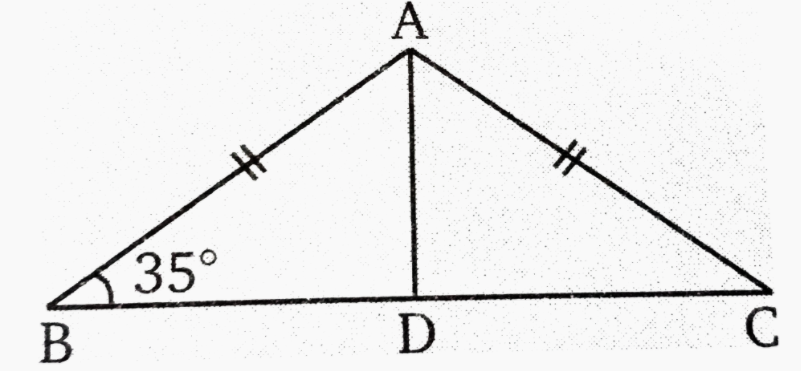
एक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AB = AC तथा AD आधार BC की माध्यिका है तब ∠BAD=
View Solutionरेखा l कोण A की समद्विभाजक है तथा l पर कोई बिंदु B है| BP और BQ बिंदु B से ∠Aकी भुजाओं पर लम्ब है तो दिखाइये कि-

(i) ΔAPB≅ΔAQB
(ii) BP=BQ
View Solutionचित्र में , AB = AC तथा BC को बढ़ाने पर कोई बिंदु D है तो सिद्ध कीजिए कि AD>AB
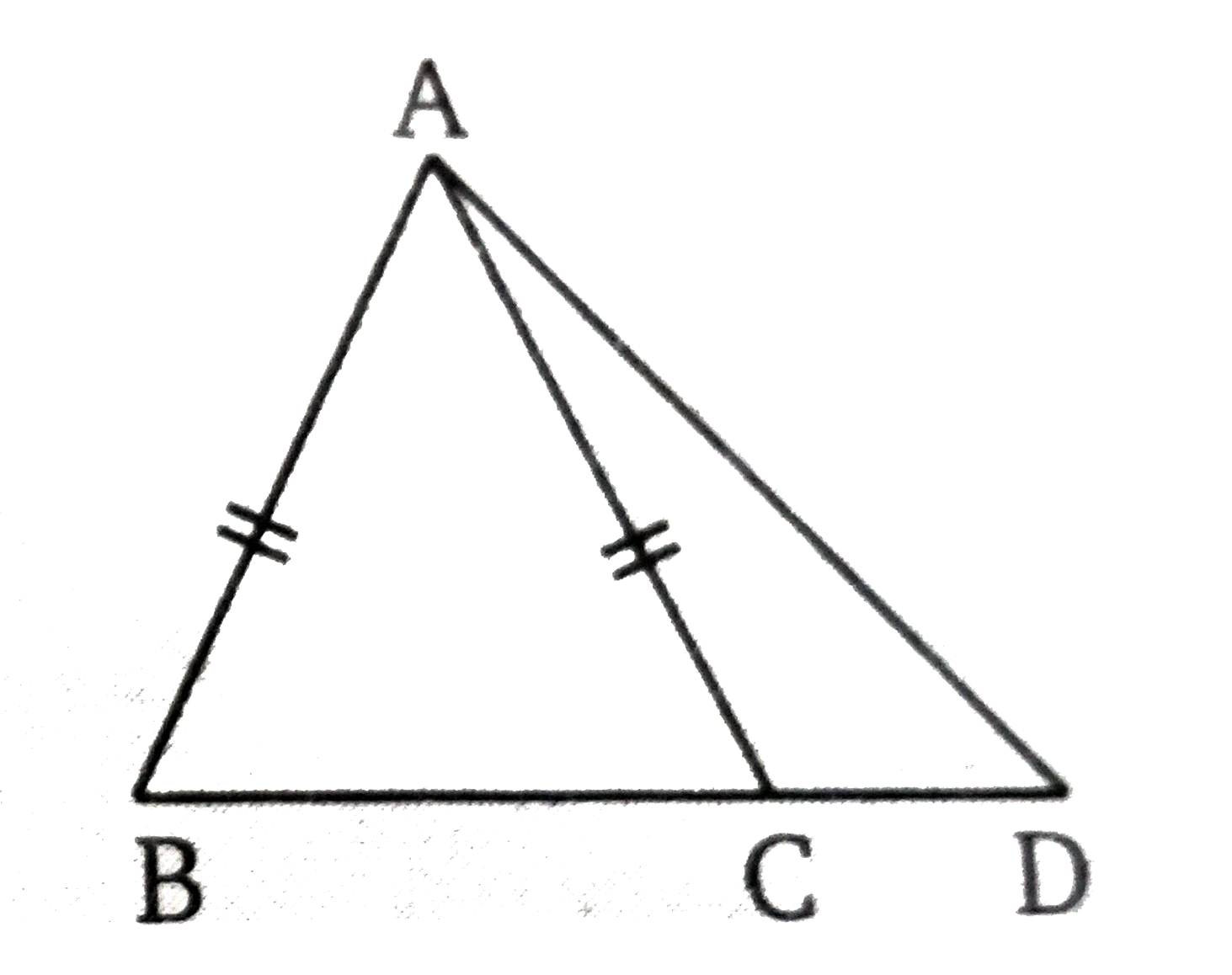
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View Solutionएक पुस्तक का मूल्य, एक पैन के मूल्य से दो गुना है | इसे व्यक्त करने के लिए दो चरो का रैखिक समीकरण लिखिये |
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=0
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionएक त्रिभुज ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AD=9 सेमी ,GE=4.2 सेमी और GC=6 सेमी ,तो AG , BE औरFG की लम्बाइयों के मान ज्ञात कीजिए।
View Solutionचित्र में AD=15 सेमी CF=23 सेमी और BE=7 सेमी तो त्रिभुज ABC कि परिमित ज्ञात कीजिए।

View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionकिसी त्रिभुज ABC की माध्यिकाएँ AD, BE, CF बिन्दु G पर मिलती हैं | दर्शाइए कि :
ΔAGB=ΔBGC=ΔCGA=13ΔABC.
View Solutionकिसी त्रिभुज की माध्यिकाएँ …………. होती है ।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solution
