माना ABCD एक समान्तर चतुर्भुर्ज है तथा AP व CQ क्रमशः बिन्दु A व C से विकर्ण पर आएले गए लम्ब है। सिद्ध कीजिए की AP=CQ
ΔAPD व ΔBQC में
AD=BC
[ ∴ABCD एक समान्तर चतुर्भुर्ज है
इसलिए AD=BC]
∠ADP=∠CBQ
[∴AD∣∣BC व BD तिर्यक रखा है
∴∠DB=∠CBD ]
अर्थात ∠ADP=∠CBQ
( एकान्तर कोण)
∠APD=∠CQB
[ प्रत्येक 90∘]
∴ΔAPD≅BQC
[∀Sसर्वांगसम]
अतः AP=CQ
[CPCT]

Topper's Solved these Questions
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.1
15 Videos
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.2
7 Videos
- घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन BOOK - BALAJI PUBLICATIONCHAPTER - घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)
13 Videos
Similar Questions
एक समान्तर चतुर्भुर्ज का के कोण संलग्न (Adjacent) कोण का 23 है । तब समान्तर चतुर्भुर्ज के कोण ज्ञात कीजिए।
View SolutionABCD एक समचतुर्भुज है। EABF एक सरल रेखा इस प्रकार है की EA=AB=BF सिद्ध कीजिए की ED व FC को बढ़ाने पर ये समकोण पर पटिच्छेद करती है ।
View Solutionमंजू अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक आयताकार बॉक्स पर रखना चाहती है । जिसे सांताक्लॉज के चित्र के साथ एक रंगीन कागज़ से ढाका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज़ खरीदना चाहिए यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई एवं ऊचाई 80 सेमी, 40 सेमी, 20 सेमी है तो उसे 40 सेमी भुजा वाली कागज़ की कितनी शीटों की आवश्यकता है।
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View SolutionABCD एक समांतर चतुर्भुज है तथा AP तथा CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं । दर्शाइए कि
(i) ΔAPB≅ΔCQD
(ii) AP=CQ
View SolutionABCD एक समांतर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं
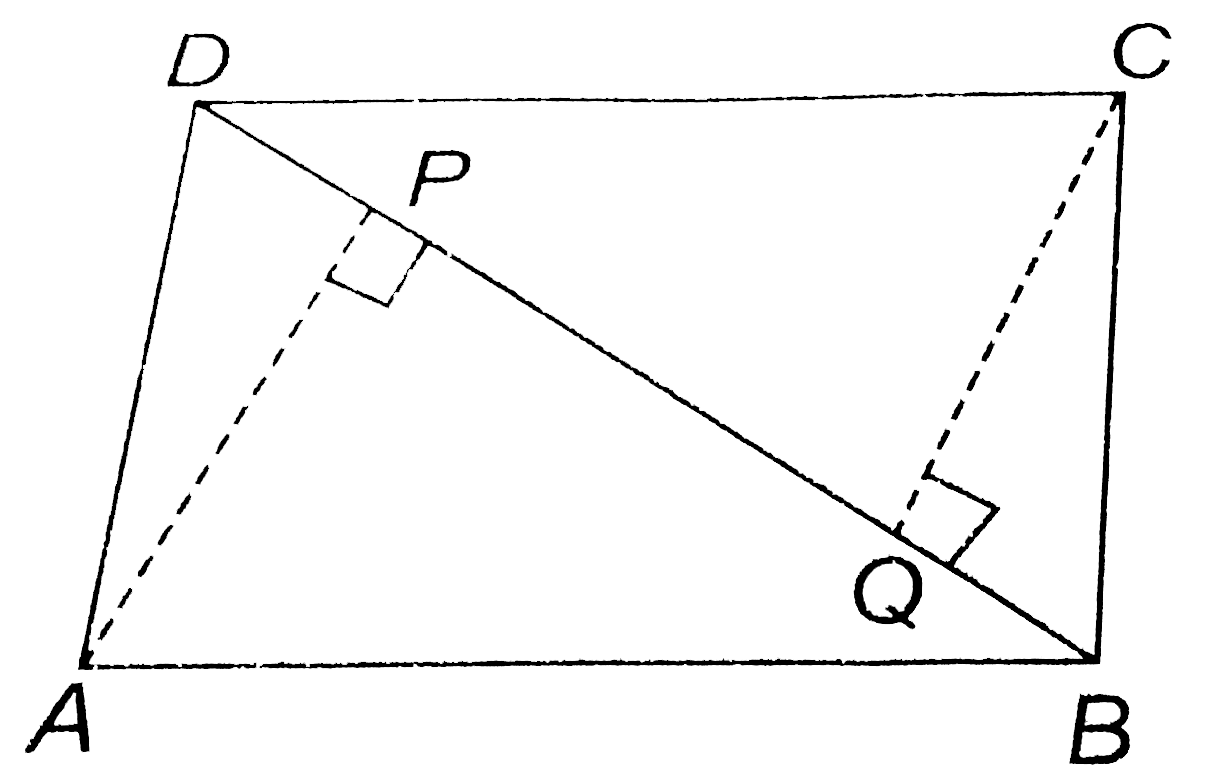
(i) ΔAPB≅ΔCQD
(ii) AP=CQ
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View SolutionABCD is a parallelogram and AP and CQ are perpendicular from vertices A and C on diagonal BD. Show that
ΔAPB≈ΔCQD
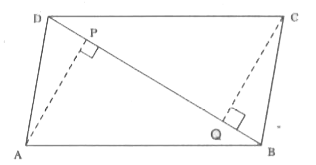
AP=CQ
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionमाना एक वृत्त है जिसका केन्द्र परवलय y2=2px की नाभि पर है, तथा यह वृत्त परवलय की नियता को स्पर्श करता है, तो वृत्त व परवलय का प्रतिच्छेद बिंदू है
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertex A and C on diagonal BD.
Show that (i) ΔAPB≅ΔCQD (ii) AP=CQ.
View SolutionABCD The quadrilateral AP and CQ show that the vertices from vertices A and C to the vertex BD are AP = CQ.
View SolutionABCD ಒಂದು ಸಮಾಂತರ ಚತುರ್ಭುಜ AP ಮತ್ತು CQ ಗಳು A ಮತ್ತು C ಶೃಂಗಗಳಿಂದ BD ಕರ್ಣಕ್ಕೆ ಎಳೆದ ಲಂಬಗಳಾಗಿವೆ. (i) △APB ≅ △CQD (ii) AP = CQ ಒಂದು ಎಂದು ತೋರಿಸಿ.
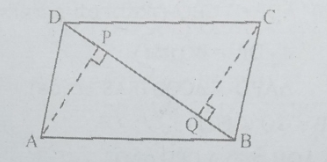
View SolutionABCD is a parallelogram AP and CQ are perpendiculars drawn from vertices A and C on diagonal BD (see figure) show that
(i) ΔAPB≅ΔCQD
(ii) AP=CQ
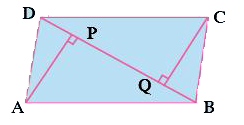
View Solution
