Question

सिद्ध कीजिए की किसी वर्ग की क्रमिक भुजाओं के युग्मों के मध्य बिंदुओं को मिलाने वाले रेखाखण्ड से बना चतुर्भुज भी एक वर्ग होता है।

Explanation

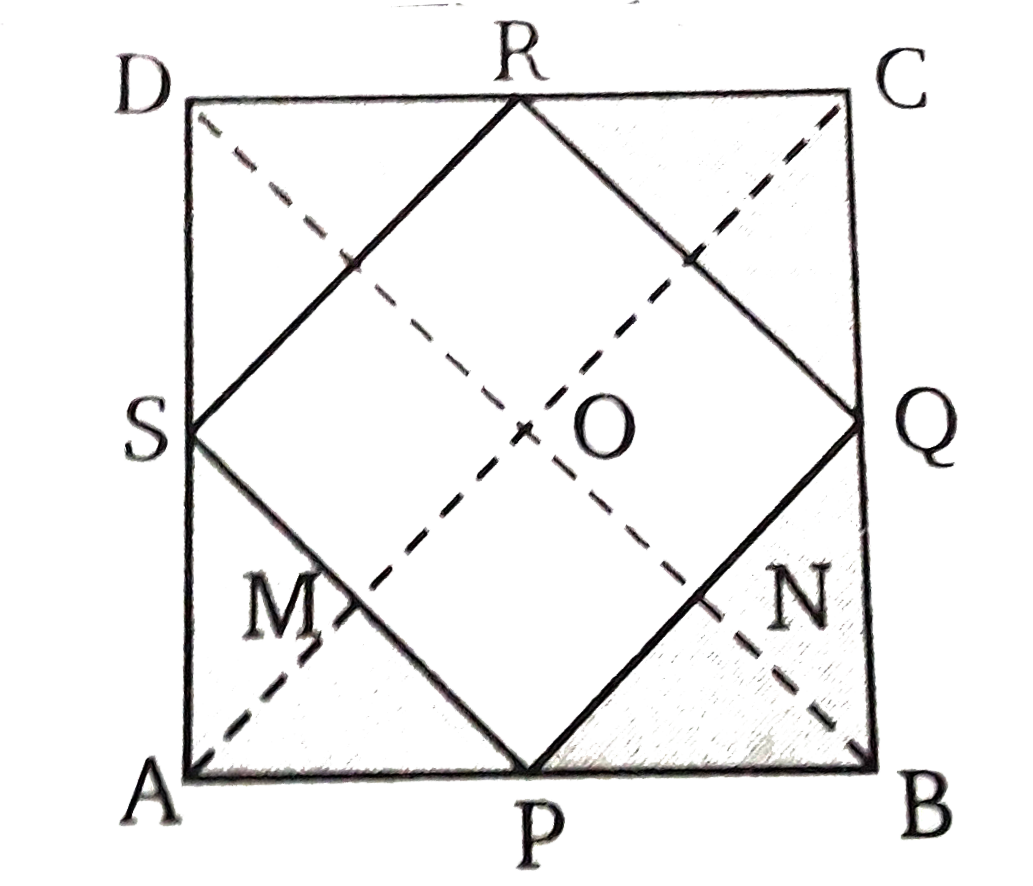
दिया है की वर्ग `ABCD` जहाँ `P,Q,R,S` क्रमशः `AB,BC,CD` व `DA` के मध्य बिन्दु है।
सिद्ध करना है: `PQRS` एक वर्ग है।
उत्पत्ति `DeltaABC` में P व Q क्रमशः`AB` व `BC` मध्य बिन्दु है।
`:. PQ||AC` व `PQ=(1)/(2)AC" "...(1)`
`DeltaADC` में, R व S क्रमशः `CD` व `AD` के मध्य बिन्दु है।
`:.RS||AC` व `RS=(1)/(2)=AC" "....(2)`

समीकरण (1) व (2) से
`PQ||RS` व `PQ=RS" "...(3)`
`:. PQRS` एक समान्तर चतुर्भुर्ज है।
अब `DeltaPBQ` व `DeltaRCQ` में
`PB=RC [ :. ABCD` एक वर्ग है `AB=BC=CD=DA]`
`BQ=CQ`
`rArr (1)/(2)AB=(1)/(2)CD` व `(1)/(2)AB=(1)/(2)BC`
`rArr PB=RC` व ` BQ=CQ`
`:.anglePBQ=angleRCQ " "` [ प्रत्येक `90^(@)`]
`:. DeltaPBQ~=DeltaRCA" "` [ SAS सर्वांगसमता से]
`:. PQ=QR " " [ CPCT] " "....(4)`
समीकरण (3) व (4) से
`PQ=QR=RS`
लेकिन `PQRS` एक समान्तर चतुर्भुर्ज है ।
`:. QR=PS`
इसलिए `PQ=QR=RS=PS " "....(5)`
अब `PQ||AC rArr PM||NO " "...(6)`
क्योकिं P व S क्रमशः `AB` व `AD` के मध्य बिन्दु है।
`:.PS||BD`
`:. PM||MO " "....(7)`
इसलिए चतुर्भुर्ज `PMNO` में,
`PM||NO " " ` [ समीकरण (6) से]
`PN||MO " " ` समीकरण (7) से]
`:.PMNO` के समान्तर चतुर्भुर्ज है।
`:. angleMNP= angleMON`
`rArr angleMNP=angleBOA`
`rArr angleMNP=90^(@)`
[ `:.` वर्ग के विकर्ण पास्पर लंबवत होते है `AC bot BD rArr angle BOA =90^(@)]`
`rArr angleQPRS=90^(@)`
अतः `PQRS` एक चतुर्भुर्ज इस प्रकार है की `PQ=QR=SP` व `angleQPRS=90^(@)`
`:. PQRS` एक वर्ग है।