सिद्ध कीजिए की एक समलम्ब चतुर्भुज के विकर्णों के मध्य बिंद्युओं को मिलाने वाले रेखाखण्ड समान्तर भुजाओं के समान्तर उनके अन्तर का आधा होता है ।
दिया है: एक समलम्ब चतुर्भुर्ज ABCD जिसमे AB∣∣DC तथा E व F क्रमशः विकर्णों AC व BD के मध्य बिन्दु है ।
सिद्ध करना है : EF||AB||DC व EF=12(AB−CD)
रचना C व E को मिलाये तथा इसे ऐसे बढ़ाये की यह AB से बिन्दु P पर मिले ।
उपपत्ति ΔCDF व ΔPBF में
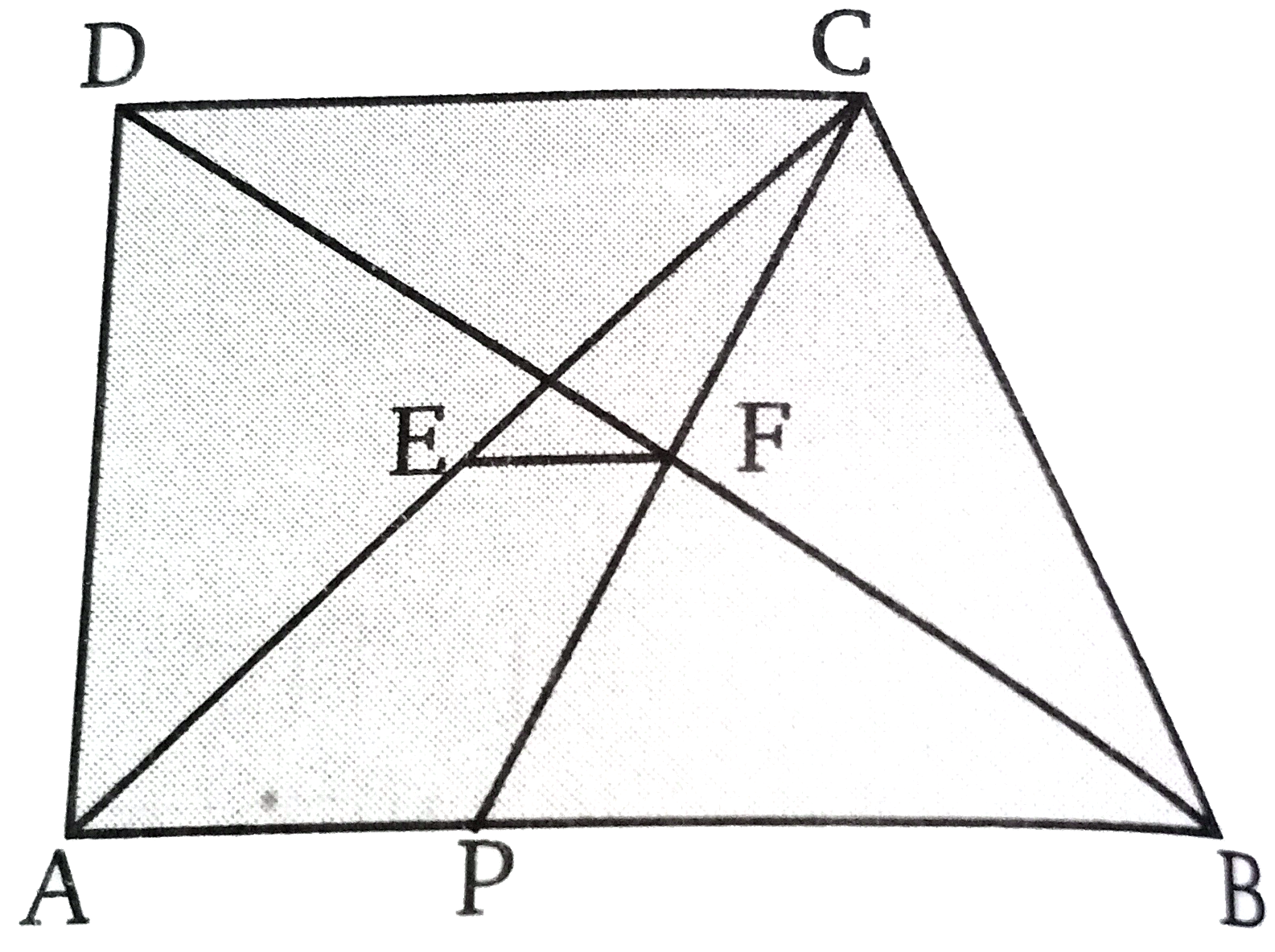
∠DCF=∠BPF [ एकान्तर कोण]
∠CDF=∠PBF [ एकान्तर कोण]
DE=FB [ F,DB का मध्य बिन्दु है]
∴ΔCDF≅ΔPBF [ AAS सर्वांगसमता से]
⇒CF=PF [CPCT]
CD=PB [CPCT]
अब ΔCAP में E व F क्रमशः CA व CP के मध्य बिन्दु है।
EF∣∣AP और EF=12AP
EF||AP⇒EF||AB∣∣DC
और EF=12AP⇒EF=12(AB−PB)=12AB−CD
अतः EF||AB||DC और EF=12(AB−CD) [∴PB=CD]
Topper's Solved these Questions
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.1
15 Videos
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.2
7 Videos
- घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन BOOK - BALAJI PUBLICATIONCHAPTER - घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)
13 Videos
Similar Questions
एक समान्तर चतुर्भुर्ज का के कोण संलग्न (Adjacent) कोण का 23 है । तब समान्तर चतुर्भुर्ज के कोण ज्ञात कीजिए।
View SolutionABCD एक समचतुर्भुज है। EABF एक सरल रेखा इस प्रकार है की EA=AB=BF सिद्ध कीजिए की ED व FC को बढ़ाने पर ये समकोण पर पटिच्छेद करती है ।
View Solutionमंजू अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक आयताकार बॉक्स पर रखना चाहती है । जिसे सांताक्लॉज के चित्र के साथ एक रंगीन कागज़ से ढाका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज़ खरीदना चाहिए यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई एवं ऊचाई 80 सेमी, 40 सेमी, 20 सेमी है तो उसे 40 सेमी भुजा वाली कागज़ की कितनी शीटों की आवश्यकता है।
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionx-अक्ष के समान्तर समतल का समीकरण है
View Solutionसमान्तर चतुर्भुज के प्रश्नो को हल करना सीखे
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View SolutionRevision|चतुर्भुज#!#चतुर्भुज के प्रकार#!#समान्तर चतुर्भुज
View Solution
