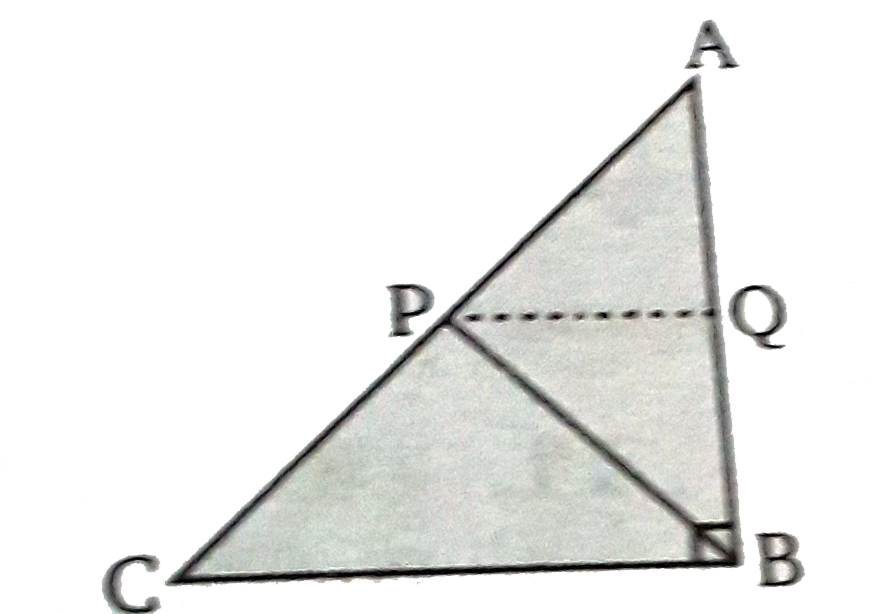
एक त्रिभुज ABC है जो B पर समकोण है तथा P,AC का माधुय बिन्दु है और तो सिद्ध कीजिए की
(i) PQ⊥AB (iii)Q,AB का मध्य बिन्दु है।
यहाँ ΔABC,B पर समकोण है।
PQ∣∣BC, खींची जो AB से Q पर मिलती है।
(i) हमे सिद्ध करना है की PQ⊥AB.
चूँकि PQ∣∣BC इसलिए
∠AQP=∠ABC (संगतबराबर कोण)
इसलिए ∠AQP=90∘
किन्तु यहाँ
∠AQP+∠BQP=180∘ (रैखिक युग्म कोण)
⇒90∘+∠BQP=180∘
⇒∠BQP=90∘
इसलिए ∠AQP=∠BQP=90∘ ......(1)
अतः PQ⊥AB
(ii) चूँकि P,AC का मध्य बिन्दु है तथा PQ∣∣BC इसलिए Q,AB का मध्य बिन्दु है अथार्त ⇒AQ=BQ
Topper's Solved these Questions
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.1
15 Videos
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - अभ्यास प्रश्न 13.2
7 Videos
- घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन BOOK - BALAJI PUBLICATIONCHAPTER - घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - स्वमूल्यांकन परिक्षण ( Self Assessment Test)
13 Videos
Similar Questions
एक समान्तर चतुर्भुर्ज का के कोण संलग्न (Adjacent) कोण का 23 है । तब समान्तर चतुर्भुर्ज के कोण ज्ञात कीजिए।
View SolutionABCD एक समचतुर्भुज है। EABF एक सरल रेखा इस प्रकार है की EA=AB=BF सिद्ध कीजिए की ED व FC को बढ़ाने पर ये समकोण पर पटिच्छेद करती है ।
View Solutionमंजू अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक आयताकार बॉक्स पर रखना चाहती है । जिसे सांताक्लॉज के चित्र के साथ एक रंगीन कागज़ से ढाका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज़ खरीदना चाहिए यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई एवं ऊचाई 80 सेमी, 40 सेमी, 20 सेमी है तो उसे 40 सेमी भुजा वाली कागज़ की कितनी शीटों की आवश्यकता है।
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solution
