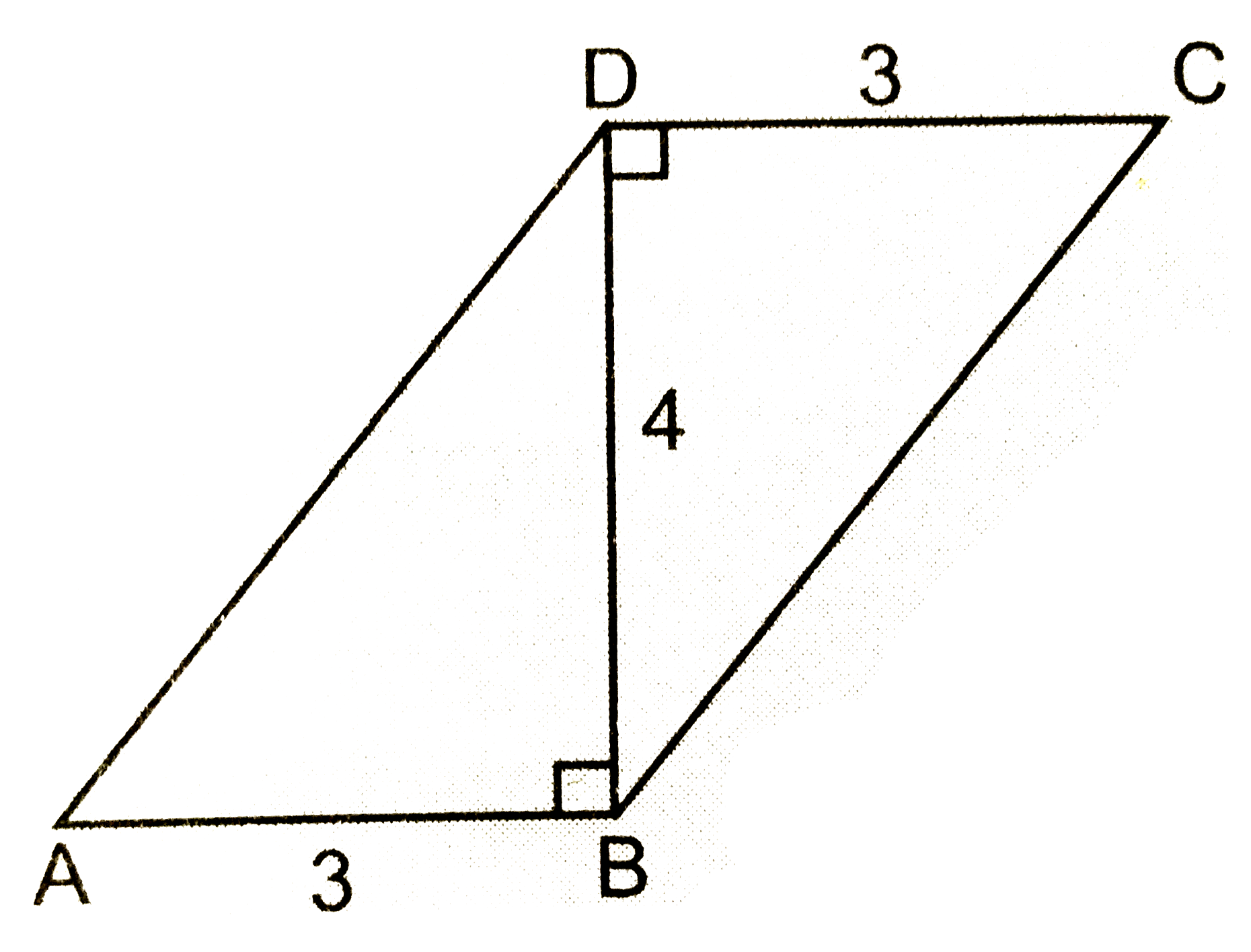
चित्र में ABCD एक चतुर्भुज है तथा BD इसका एक विकर्ण है । सिद्ध कीजिए कि ABCD एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ज्ञात कीजिए।
12 सेमी2
15 सेमी2
24 सेमी2
14 सेमी2
The correct Answer is:A
दिए गये चतुर्भुज ABCD में
AB=DC=3,BD=4 व ∠B=∠D=90∘
∵ विकर्ण BD, AB व DC को प्रतिच्छेद करता है।
∠ABD=∠BDC=90∘ [दिया है]
AB∣∣CD
[∵∠ABD व ∠BDC एकांतर कोण है ]
व AB=DC=3 [दिया है]
⇒ABCD एक समांतर चतुर्भुज है।
हम जानते हैं कि
समांतर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्षलम्ब
=3×4=12 वर्ग इकाई
Topper's Solved these Questions
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - अति लघु उत्तरीय प्रश्न
5 Videos
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - लघु उत्तरीय प्रश्न
16 Videos
- शेषफल प्रमेय तथा गुणनखण्ड प्रमेय BOOK - BALAJI PUBLICATIONCHAPTER - शेषफल प्रमेय तथा गुणनखण्ड प्रमेय EXERCISE - स्वमूल्यांकन परिक्षण
20 Videos
- सांख्यिकीBOOK - BALAJI PUBLICATIONCHAPTER - सांख्यिकीEXERCISE - स्वमूल्यांकन परीक्षण
17 Videos
Similar Questions
एक समांतर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
View Solutionचित्र (i) और (ii) में दिए गये समलम्ब चतुर्भुजों ABCD और PQRS का क्षेत्रफल ज्ञात कीजिए।

View Solutionx3+3x2+3x+1 को 5+2x से भाग करने पर शेषफल ज्ञात कीजिए।
View Solutionतीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चित् की संख्या निम्न प्रकार लिखी गयी :
0,1,2,2,1,2,3,1,3,0,1,3,1,1,2,2,0,1,2,1,3,0,0,1,1,2,3,2,2,0
उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solution