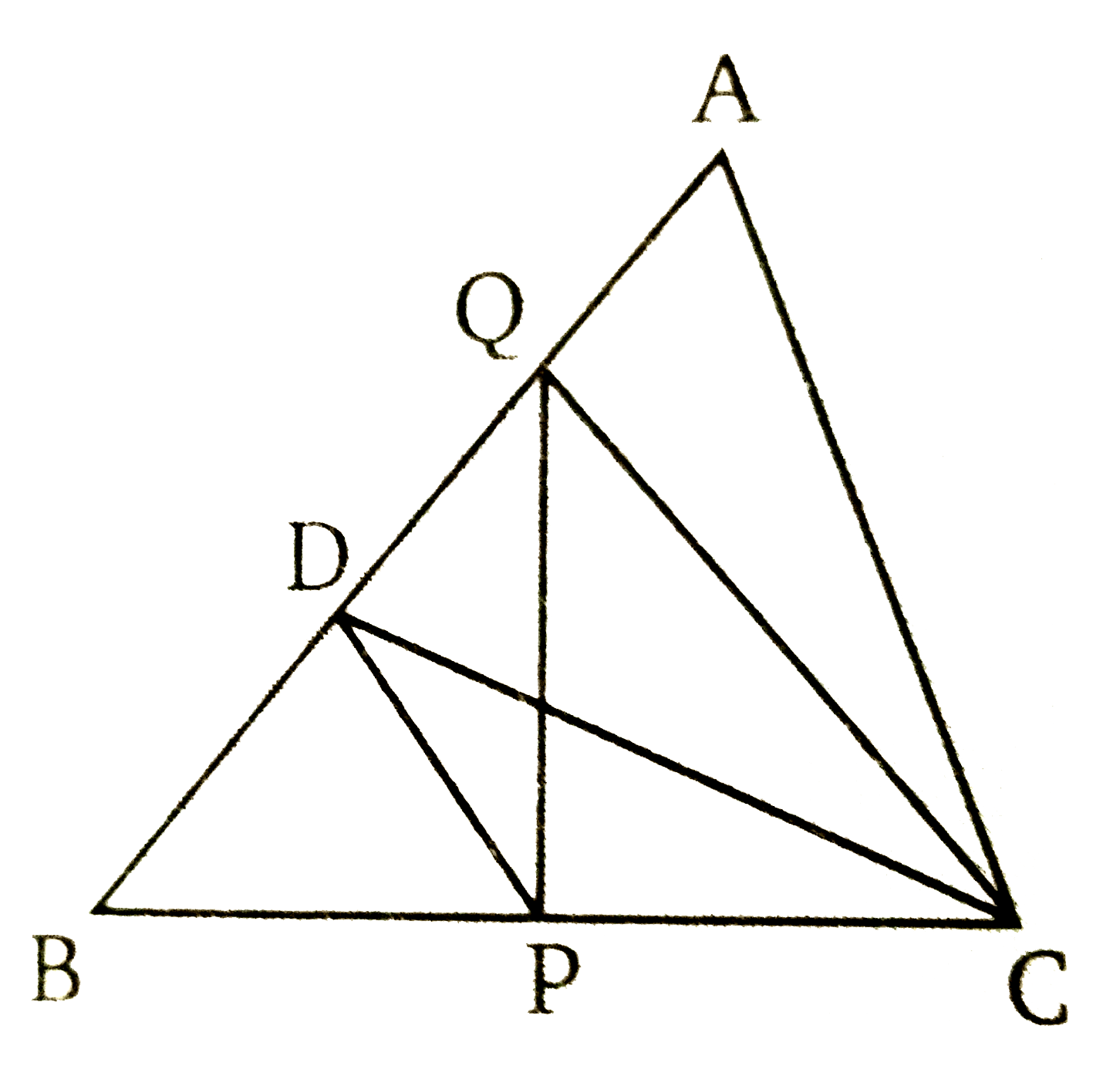
ΔABC में D भुजा AB का मध्य बिंदु है तथा P,BC पर कोई बिंदु है CQ∣∣PD,AB के बिंदु Q पर मिलती है। सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
रचना: CD को मिलायें।
उपपत्ति: क्योंकि D भुजा AB का मध्य बिंदु है।
∴ΔABC में CD माध्यिका है इसलिए
ar(ΔBCD)=12ar(ΔABC)....(i)
चूंकि ΔPDQ व ΔPDC समान आधार PD व समान समांतर रेखाओें PD व QC के बीच हैं।
ar(ΔPDQ)=ar(ΔPDC)…(ii)
समीकरण (i) से
ar(ΔBCD)=12ar(ΔABC)
⇒ar(ΔBPD)+ar(ΔPDC)=12ar(ΔABC)
⇒ar(ΔBPD)+ar(ΔPDQ)=12ar(ΔABC)
[समीकरण (ii) से]
अतः ar(ΔBPQ)=12ar(ΔABC)
Topper's Solved these Questions
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBook:BALAJI PUBLICATIONChapter:समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलExercise:अति लघु उत्तरीय प्रश्न
Explore 5 Videos
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBook:BALAJI PUBLICATIONChapter:समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलExercise:लघु उत्तरीय प्रश्न
Explore 16 Videos
- शेषफल प्रमेय तथा गुणनखण्ड प्रमेय Book:BALAJI PUBLICATIONChapter:शेषफल प्रमेय तथा गुणनखण्ड प्रमेय Exercise:स्वमूल्यांकन परिक्षण
Explore 20 Videos
- सांख्यिकीBook:BALAJI PUBLICATIONChapter:सांख्यिकीExercise:स्वमूल्यांकन परीक्षण
Explore 17 Videos
Similar Questions
एक समांतर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
View Solutionचित्र (i) और (ii) में दिए गये समलम्ब चतुर्भुजों ABCD और PQRS का क्षेत्रफल ज्ञात कीजिए।

View Solutionx3+3x2+3x+1 को 5+2x से भाग करने पर शेषफल ज्ञात कीजिए।
View Solutionतीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चित् की संख्या निम्न प्रकार लिखी गयी :
0,1,2,2,1,2,3,1,3,0,1,3,1,1,2,2,0,1,2,1,3,0,0,1,1,2,3,2,2,0
उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionनिर्देशाक्षो को प्रारंभिक निर्देशांकों के समांतर रखते हुए मूल बिंदु को बिंदु P पर हटाने पर समीकरण ax+by+c=0 समीकरण ax+by+c+λ=0 के रूप में बदल जाता है सिद्ध कीजिए कि P बिन्दुपथ ax+by=λ होगा ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
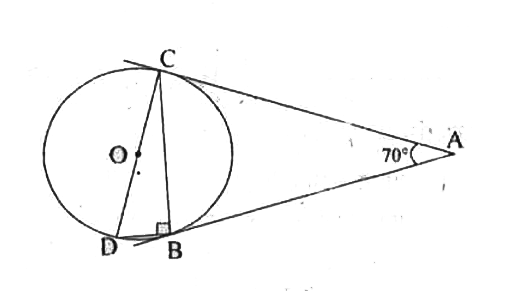
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View SolutionAB एक ऊर्ध्वाधर खंभा है, जिनका A सिरा जमीन पर है | C, AB का मध्य-बिंदु है और P जमीन पर एक बिंदु है | BC, बिंदु P पर β कोण बनता है | यदि AP = nAB हो, तो tanβ का मान है |
View Solution
