किसी व्यापारी संघ के पास रू0 30,000 का कोष है जिसे दो भिन्न-भिन्न प्रकार के बांडों में निवेशित करना है। प्रथम बांड पर 5 प्रतिशत वार्षिक और द्वितीय बांड पर 7 प्रतिशत वार्षिक ब्याज प्राप्त होता है। आव्यूह गुणन के प्रयोग द्वारा निर्धारित कीजिए कि रू0 30,000 के कोष को दो प्रकार के बांडों में निवेश करने के लिए किस प्रकार बांटे जिससे व्यापार संघ को कुल वार्षिक ब्याज (a) Rs. 1800 हो (b) Rs. 2000 प्राप्त हो।
माना =Rs.30,000 के दो भाग Rs. x और Rs. (30,000−x) है।
निवेश आव्यूह A=[x30000−x]
प्रथम बांड पर वार्षिक ब्याज दर =5%=5100=0.05
द्वितीय बांड पर वार्षिक दर =7%=7100=0.07
वार्षिक ब्याज हेतु आव्यूह B=[0.050.07]
∴ कुल ब्याज =AB
=[x3000−0−x][0.050.07]
=[(0.05x+(30000−x)×0.07)]
=[0.05x+2100−0.07x]
=[2100−0.02x]
=[2100−0.02x]
a. वार्षिक ब्याज हेतु समीकरण है
2100−0.02x=1800
⇒0.02x=300
⇒x=3000.02=300002=Rs.15000
∴30000−x=30000−15000=Rs.15000
अतः रू0 18000 ब्याज पाने के लिए प्रत्येक बाण्ड रू0 15000 के खरीदने चाहिए।
b. रू0 2000 वार्षिक ब्याज हेतु समीकरण है-
2100−0.02x=2000
⇒0.02x=100
⇒x=1000.052=100005=5000
अतः रू0 2000 ब्याज पाने के लिए रू0 30000 के दो बाण्डों रू0 50000 व रू0 25000 करने होंगे।
Topper's Solved these Questions
- आव्यूहBOOK - PRABODH PUBLICATIONCHAPTER - आव्यूहEXERCISE - प्रश्नावली 1
13 Videos
- आव्यूहBOOK - PRABODH PUBLICATIONCHAPTER - आव्यूहEXERCISE - प्रश्नावली 2
10 Videos
- अवकलनीयता BOOK - PRABODH PUBLICATIONCHAPTER - अवकलनीयता EXERCISE - प्रतियोगी परीक्षा हेतु विविध प्रश्नावली
3 Videos
- आव्यूह के सहखण्डज और व्युत्क्रम BOOK - PRABODH PUBLICATIONCHAPTER - आव्यूह के सहखण्डज और व्युत्क्रम EXERCISE - वस्तुनिष्ट प्रश्न
8 Videos
Similar Questions
निम्नलिखित आव्यूहों के क्रम ज्ञात कीजिए-
A=[354−20√3−149]
View Solutionनिम्नलिखित समीकरणों से x,y तथा z के मान ज्ञात कीजिएः
[43x5]=[yz15]
View Solutionअचर m का निर्धारण कीजिए जबकि फलन
f(x)={m(x2−2x),x<0cosx,x≥0 संतत है।
View Solutionनिम्न में सत्य कथन है
View Solutionएक कम्पनी दो प्रकार के टेलीफ़ोन A व B बनाती है|A प्रकार के टेलीफ़ोन बनाने में 2 घण्टे एवं 300 टेलीफोनों को एक दिन में पैक किया जा सकता है| A प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 400 है| अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफ़ोन का निर्माण करती है तो रेखीय प्रतिबन्ध (x≥0,y≥0 के अलावा ) है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त क्षेत्र के शीर्ष है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|
View Solutionमीरा के पदों के आधार पर स्पष्ट कीजिए कि वह भक्त की विपत्ति दूर करने के लिए किन प्रसंगों की याद कृष्ण को दिखाती है और उन्हें पाने के लिए क्या-क्या कार्य करने को तत्पर है?
View Solutionआव्यूह के प्रकार पर आधारित महत्वपूर्ण प्रश्न
View Solutionकिस प्रकार के समाचारों में शब्द, ध्वनि और दृश्य तीनों का मेल होता है?
View Solutionगरुभूमि के इलाके में वर्षा की मात्रा नापने के लिए किस इकाई.का प्रयोग होता है?
View Solutionकिस प्रकार के समाचारों में शब्द, ध्वनि और दृश्य तीनों का मेल होता है?
View SolutionThe table given below presents the figures of the production (in thousands) of different types of vehicles by a company during the year 2013-18.
नीचे दी गयी तालिका वर्ष 2013-18 के दौरान एक कंपनी के द्वारा विभिन्न प्रकार के वाहनों के उत्पादन ( हज़ार में)के आंकड़ों को प्रस्तुत करती है |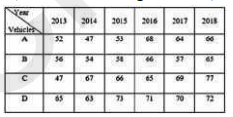 The total production of all types of vehicles in 2018 is what percent more than the total production of all types of vehicles in 2015?
The total production of all types of vehicles in 2018 is what percent more than the total production of all types of vehicles in 2015?
2018 में सभी प्रकार के वाहनों का कुल उत्पादन 2015 में सभी प्रकार के वाहनों के कुल उत्पादन से कितना प्रतिशत अधिक है ?
View Solutionनिम्नलिखित में से कौन-सा प्रश्न बच्चों की भाषा-क्षमता के विकास में सर्वाधिक सहायक है?
View Solutionत्रिभुज के प्रकार #!#त्रिभुज के भिन्न केंद्र
View Solution
