A series combination of $n_{1}$ capacitors, each of value $C_{1}$ , is charged by a source of potential difference $4 V$ . When another parallel combination of $n_{2}$ capacitors, each of value $C_{2}$ , is charged by a source of potential difference $V$ , it has same (total) energy stored in it, as the first combination has. the value of $C_{2}$ , in terms of $C_{1}$ , is then

A

$\frac{2 C_{1}}{n_{1} n_{2}}$

B

$16 \frac{n_{2}}{n_{1}} C_{1}$

C

$2 \frac{n_{2}}{n_{1}} C_{1}$

D

$\frac{16 C_{1}}{n_{1} n_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

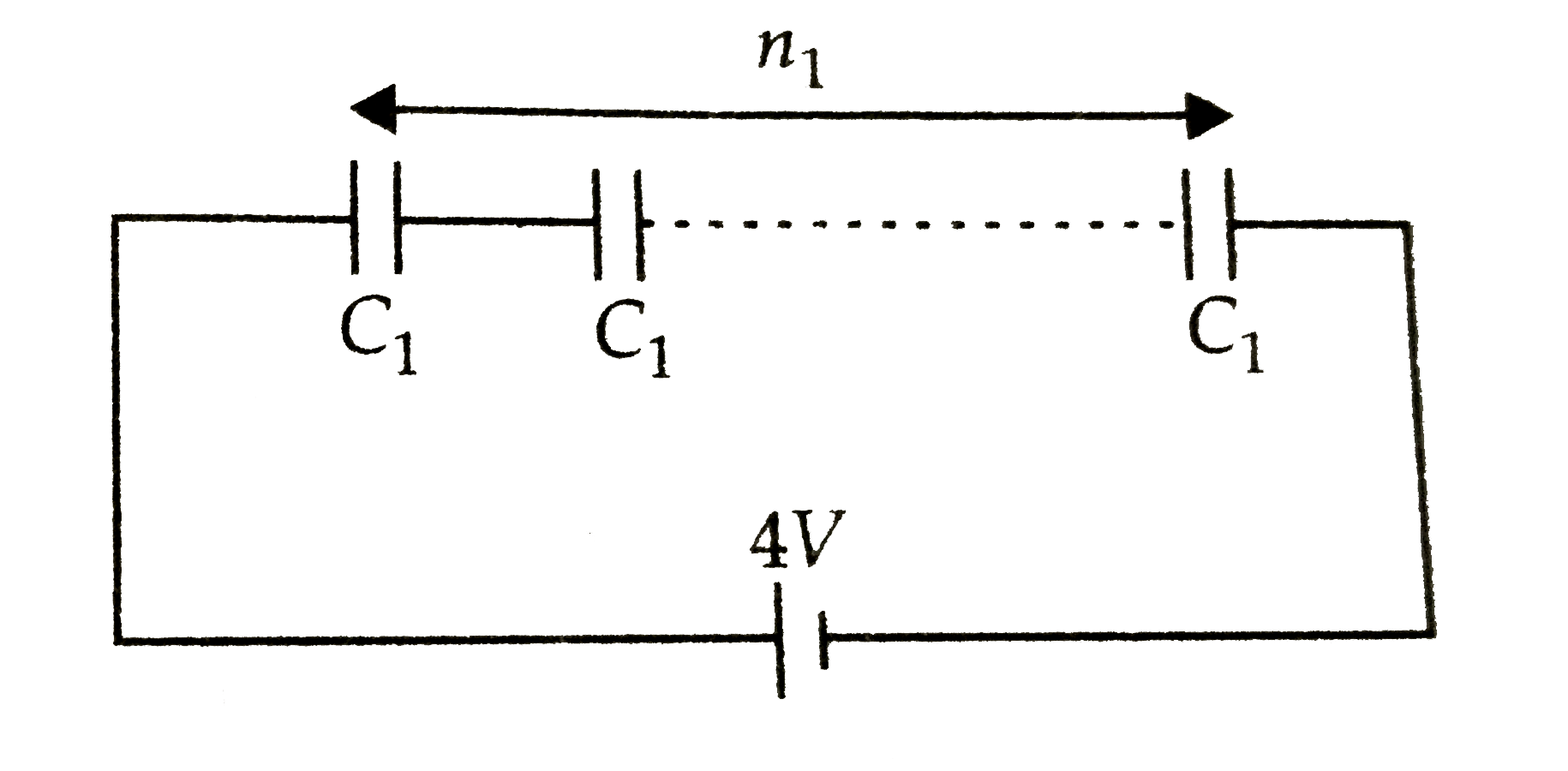
A series combination of $n_{1}$ capacitors each of capacitance $C_{1}$ are connecte to 4V source as shown in the figure .
Total capaciture of the series combination of the capacitors is given by .
$U_{s} = \frac{1}{2} C_{s} {(4 V)}^{2} = \frac{1}{2} (\frac{C_{1}}{n_{1}}) {(4 V)}^{2} (Using (i))......(ii))$
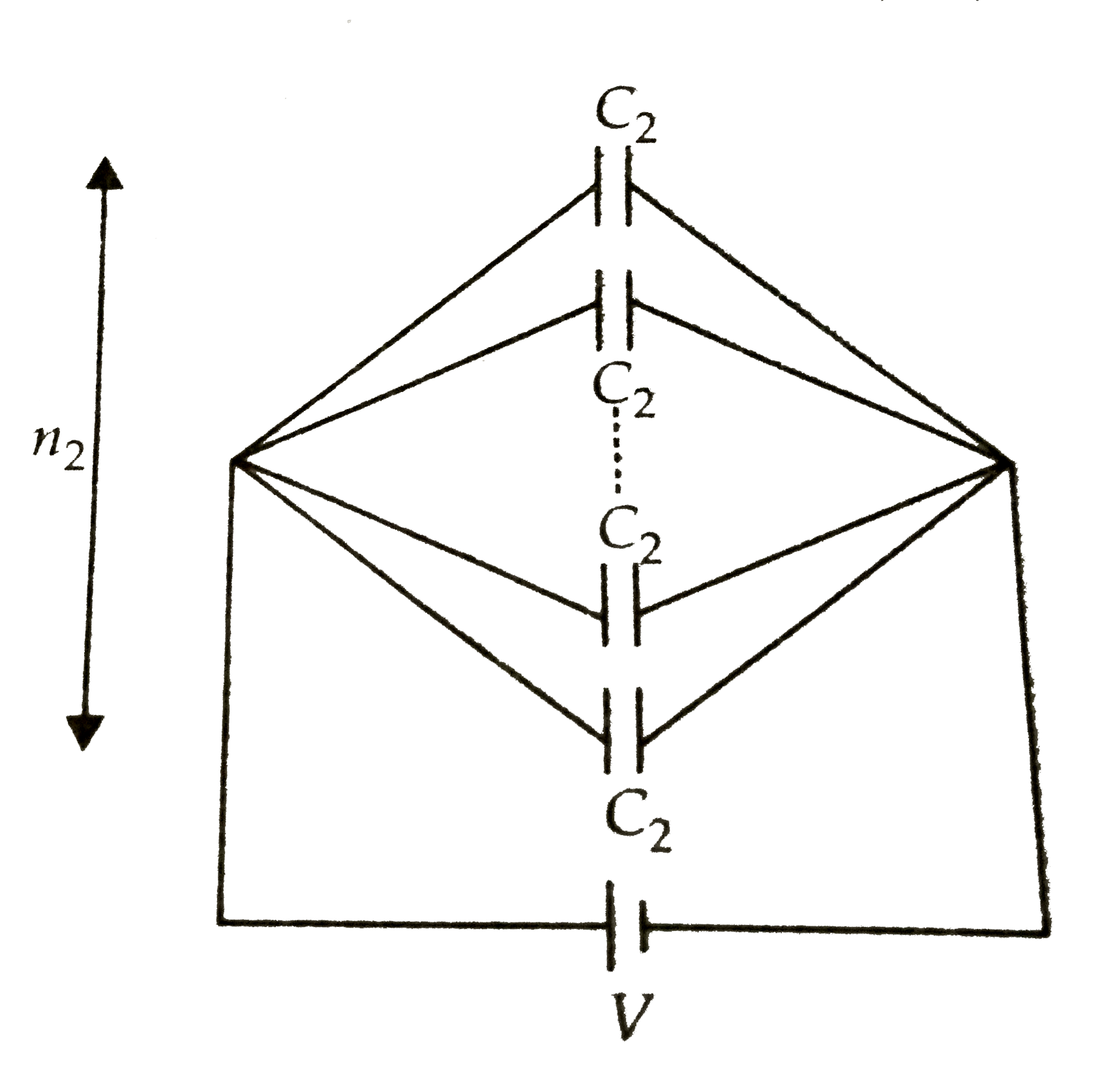
A parallel combination of $n_{2}$ capacitors each of capacitance $C_{2}$ are connected to V source to V source as shown in the figure.
Total energy stored in a parallel combintion of capacitors is $U_{p} = \frac{1}{2} C_{p} V^{2} = \frac{1}{2} (n_{2} C_{2}) {(V)}^{2} (Using (iii)) ... . . (i v)$
According to the given problem, $U_{s} = U_{p}$
$\frac{1}{2} \frac{C_{1}}{n_{1}} {(4 v)}^{2} = \frac{1}{2} (n_{2} C_{2}) {(V)}^{2}$
or $\frac{C_{1} 16}{n_{1}} = n_{2} C_{2} or C_{2} = \frac{16 C_{1}}{n_{1} n_{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A series combination of $N_{1}$ capacitors (each of capacity $C_{1}$ ) is charged to potential difference 3V. Another parallel combination of $N_{2}$ capacitors (each of capacity $C_{2}$ ) is charged to potential difference V. The total energy stored in both the combinations is same, The value of $C_{1}$ in terms of $C_{2}$ is
A $\frac{C_{2} N_{1} N_{2}}{9}$
B $\frac{C_{2} N_{1}^{2} N_{2}^{2}}{9}$
C $\frac{C_{2} N_{1}}{9 N_{2}}$
D $\frac{C_{2} N_{2}}{9 N_{1}}$
Question 2 - Select One
Parallel combination of two capacitors, each of value $10 μ F$ is charged by 200 volt d.c. Total energy of the capictor in joules will be :
A0.1
B0.2
C0.4
D0.6
Question 3 - Select One
A capacitor or capacitance $C_{1}$ is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance $C_{2}$ . The fianl potential difference across each capacitor will be
A $\frac{C_{1} V}{C_{1} + C_{2}}$
B $\frac{C_{2} V}{C_{1} + C_{2}}$
C $1 + \frac{C_{2}}{C_{1}}$
D $1 - \frac{C_{2}}{C_{1}}$

NCERT FINGERTIPS-ELECTROSTATIC POTENTIAL AND CAPACITANCE -Energy Stored In Capacitor

Home
Ask Doubt
Profile