A 2 m long solenoil with diameter 2 cm and 2000 turns has a secondary coil of 1000 turns wound closely near its midpoint. The mutuat inductance between the two coils is.
2.4×10−4H
3.9×10−4H
1.28×10−3H
3.14×10−3H
The correct Answer is:B
To find the mutual inductance between the solenoid and the secondary coil, we can follow these steps:
1. Identify Given Data:
- Length of the solenoid (l) = 2 m
- Diameter of the solenoid = 2 cm = 0.02 m
- Number of turns in the solenoid (N1) = 2000 turns
- Number of turns in the secondary coil (N2) = 1000 turns
2. Calculate the Radius of the Solenoid:
- Radius (r) = Diameter / 2 = 0.02 m / 2 = 0.01 m
3. Calculate the Area of Cross-section of the Solenoid:
- Area (A) = πr²
- A = π(0.01 m)² = π(0.0001 m²) = π × 10⁻⁴ m²
4. Use the Formula for Mutual Inductance (M):
- The formula for mutual inductance is:
M=μ0N1N2Al
- Where:
- μ0 (permeability of free space) = 4π×10−7H/m
5. Substitute the Values into the Formula:
- M = 4π×10−7H/m×2000×1000×π×10−42
6. Calculate the Mutual Inductance:
- First, calculate the numerator:
2000×1000×π×10−4=2×106×π×10−4=2π×102
- Now substitute back:
M=4π×10−7×2π×1022
- Simplifying gives:
M=4π×10−7×π×102=4π2×10−5H
- Using π≈3.14:
M≈4×(3.14)2×10−5≈4×9.86×10−5≈3.94×10−4H
7. Final Answer:
- The mutual inductance M≈3.94×10−4H, which corresponds to the option 3.9×10−4H.
- Length of the solenoid (l) = 2 m
- Diameter of the solenoid = 2 cm = 0.02 m
- Number of turns in the solenoid (N1) = 2000 turns
- Number of turns in the secondary coil (N2) = 1000 turns
- Radius (r) = Diameter / 2 = 0.02 m / 2 = 0.01 m
- Area (A) = πr²
- A = π(0.01 m)² = π(0.0001 m²) = π × 10⁻⁴ m²
- The formula for mutual inductance is:
M=μ0N1N2Al
- Where:
- μ0 (permeability of free space) = 4π×10−7H/m
- M = 4π×10−7H/m×2000×1000×π×10−42
- First, calculate the numerator:
2000×1000×π×10−4=2×106×π×10−4=2π×102
- Now substitute back:
M=4π×10−7×2π×1022
- Simplifying gives:
M=4π×10−7×π×102=4π2×10−5H
- Using π≈3.14:
M≈4×(3.14)2×10−5≈4×9.86×10−5≈3.94×10−4H
- The mutual inductance M≈3.94×10−4H, which corresponds to the option 3.9×10−4H.
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Ac Generator4videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - HIGHER ORDER THINKING SKILLS8videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Eddy Currents4videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason15videos
ELECTROMAGNETIC WAVES
Similar Questions
A 2 m long solenoid with diameter 4 cm and 2000 turns has a secondary of 1000 turns wound closely near its mid point. Calculate the mutual inductance between the two coils.
View SolutionA 100 cm long solenoid having diameter 2 cm and 1000 turns has a primary solenoid closely wound near its mid point. If the coefficient of mutual inductance between the coils is 0.002 H, then find the number of turns in secondary coil.
View Solution
Knowledge Check
- Question 1 - Select One
For a solenoid having a primary coil of N1 turns and a secondary coil of N2 turns, the coefficient of mutual inductance is
Aμ0μrN1N2lBμ0μrN1N2AlCμ0μrN1N2AlDμ0μrN1N2Al - Question 2 - Select One
A current of 3A, in one coil, causes a flux in the second coil of 2000 turns to change by 6×10−4Wb per turns of the secondary coil. The mutual inductance of the pair of coils is
A6 HB2 HC0.4 HD4 H - Question 3 - Select One
If number of turns in primary and secondary coils is increased to two times each, the mutual inductance
Abecomes 4 timesBbecomes 2 timesCbecomes 1/4 timesDremains unchanged
Over a solenoid of 50 cm length and 2 cm radius having 500 turns. Is wound another wire of 50 turns near the centre. Calculate mutual inductance of the two coils. If currents in primary changes From 0 to 5 a in 0.02 s, what is the emf induced in secondary coil ?
View SolutionA solenoid is of length 50cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA long solcnoid of length 1m, cross-sectional area 10cm2, having 1000 turns has wound about its centre a small coil of 20 turns. Compute the mutual inductance of the pair of solenoid and the coil . What is the induced EMF in the coil when the current in the solenoid changes at the rate of 10A/s?
View SolutionA long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
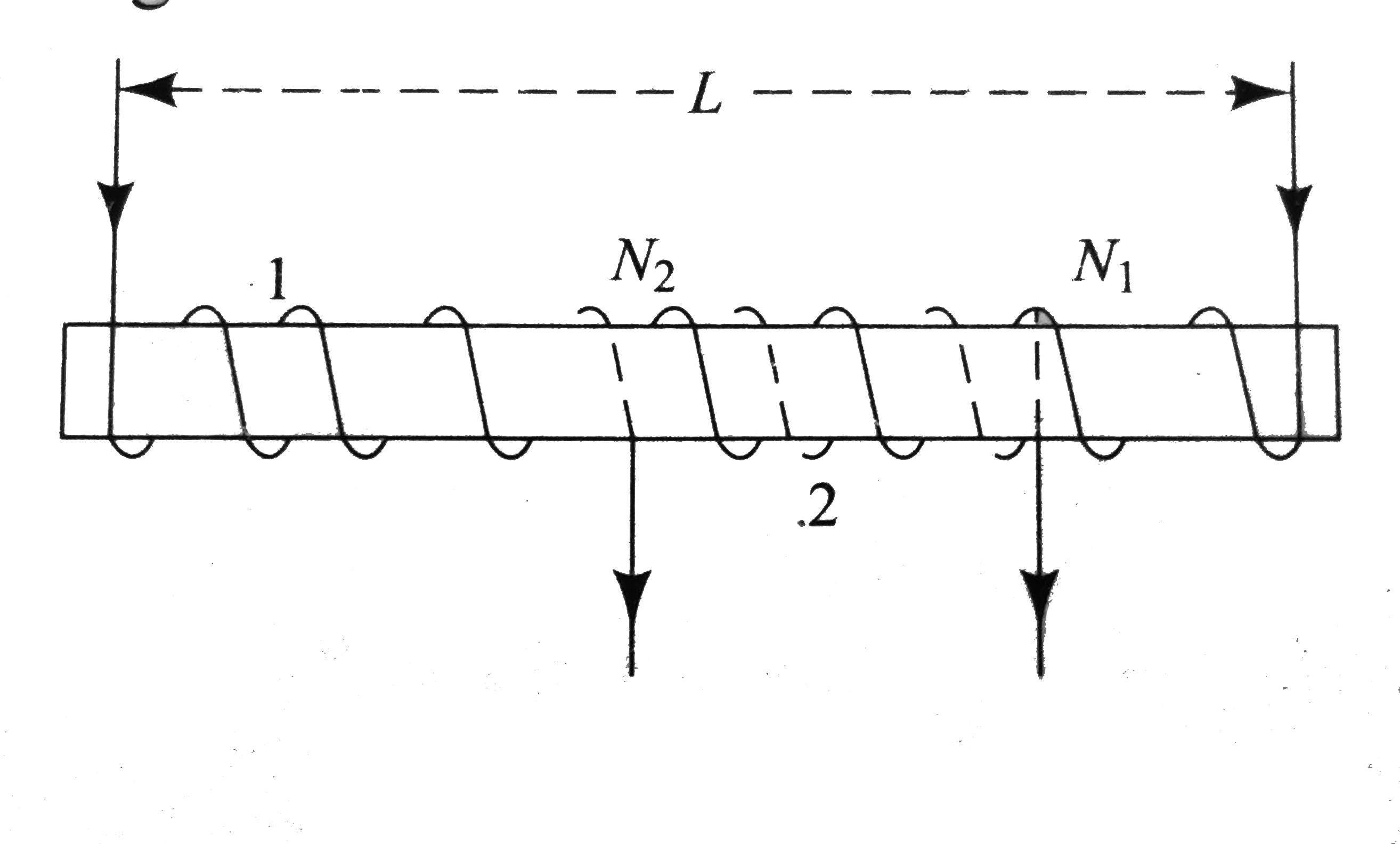 View Solution
View Solution

