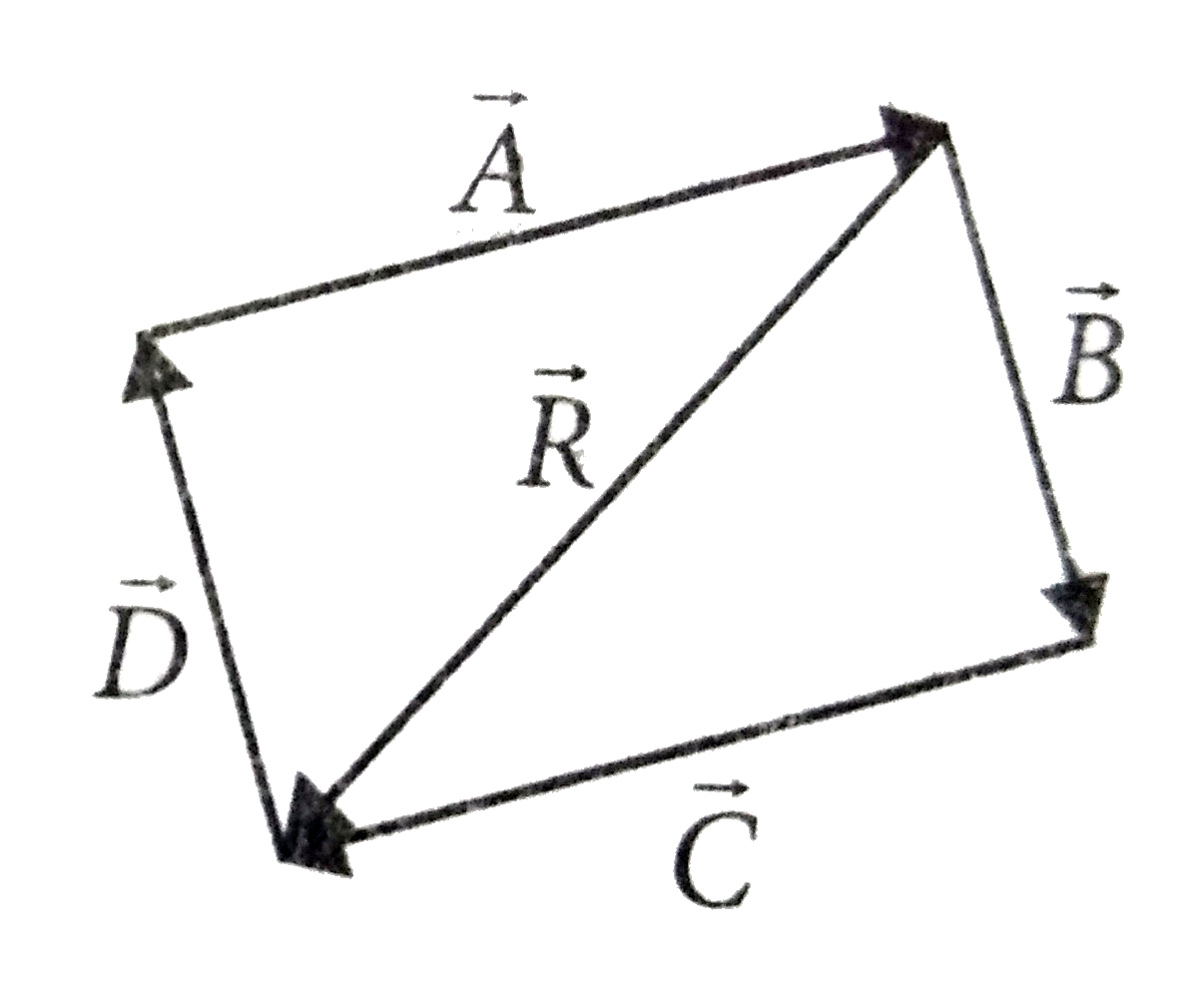
Given →A+→B+→C+→D=→0, which of the following statements is not correct ?
→A,→B,→Cand→D must each be a null vector.
The magnitude of (→A+→C) equals the magnitude of (→B+→D).
The magnitude of →A can never be greater than the sum of the magnitudes of →B,→Cand→D.
→B+→C must lie in the plane of →Aand→D if →Aand→D are not collinear and in the line of →Aand→D, if they are collinear.
The correct Answer is:A
The statement is not correct. It is because →A+→B+→C+→D can be zero in many ways other than →A,→B,→Cand→D being each a rull vector.
(b) The statement is correct as proved below
→A+→B+→C+→D=→0or→A+→C=−(→B+→D)
∴∣∣→A+→C∣∣=∣∣→B+→D∣∣
(c ) The statement is correct and can be proved using triangular inequality.
∣∣→B∣∣+∣∣→C∣∣≥∣∣→R∣∣ ...(i)
∣∣→R∣∣+∣∣→D∣∣≥∣∣→A∣∣ ...(ii)
Using (i) and (ii), ∣∣→A∣∣≤∣∣→B∣∣+∣∣→C∣∣+∣∣→D∣∣
(d) THe statement is correct as proved below
→A+→B+→C+→D=→0or→A+(→B+→C)+→D=→0
The resultant sum of three vectors →A,(→B+→C) and →D can be zero only if (→B+→C) lies in the plane of →Aand→D and these three vectors are represented by the three sides of a triangle taken in one order. IF →Aand→D are collinear, then (→B+→C) must be in the line of →Aand→D, only then the vector sum of all the vectors will be zero.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Resolution Of Vectors
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Vector Addition - Analytical Method
11 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Let →a,→b,→c be three unit vectors such that 3→a+4→b+5→c=→0. Then which of the following statements is true? (A) →a is parrallel to vecb(B)vecaisperpendica––r→→b (C) →a is neither parralel nor perpendicular to →b (D) →a,→b,→c are copalanar
View SolutionLet →a,→b,→c be unit such that →a+→b+→c=→0. Which one of the following is correct? (A) →a×→b=→b×→c=→c×→a=→0 (B) →a×→b=→b×→c=→c×→a≠→0 (C) →a×→b=→b×→c=→×→c≠→0 (D) →a×→b,→b×→c,→c×→a are mutually perpendicular
View Solution
Knowledge Check
Let →a,→b,→c be unit vetors such that →a+→b+→c=→0 , which one of the following is correct ?
A→a×→b=→b×→c=→c×→a=→0B→a×→b=→b×→c=→c×→a≠→0C→a×→b=→b×→c=→a×→c=→0D→a×→b,→b×→c,→c×→a are mutually perpendicular vectors.Two vectors →A and →B are such that →A+→B=→C and A2+B2=C2. Which of the following statements, is correct:-
AA is parallel to BBA is antiparallel to BCA is perpendicular to BDA and B are equal in magnitudeIf (→a×v→b)×(→c×→d).(→a×→d)=0 then which of the following may be true ?
A→a,→band→d are nenessarily coplanarB→a lies iin the plane of →cand→dC→vb lies in the plane of →aand→dD→c lies in the plane of →aand→d
Given a+b+cd+c=0 , which of the following statements are correct?
(a) →a,→b,→cand→d must each be a null vector .
(b) The magnitude of (→a+→c) equals the magnitude of (b+d)
(c) The magnitude of →a can never be greater than the sum of the magnitudes of →b,→cand→c.
(d) →b+→c must lie in the plane of →aand→d if →aand→d are not collinear ,and in the line of →aand→d, if they are collinear.
View SolutionGiven the following information about the non zero vectors →A,→Band→C
(i) (A→A×→B)×→A=→0 (ii) →B.→B=4 (iii) →A.→B=−6 (iv) →B.→C=6 Which one of the following does not hold good ?
View SolutionConsider the following statements in respect of a vector →c=→a+→b ,where |→a|=∣∣→b∣∣≠0:
1. →c is perpendicular to (→a−→b)
2. →c is perpendicular to (→a×→b)
Which of the above statements is/are correct?
View SolutionGiven →C=→A×→Band→D=→B×→A. What is the angle between →C and →D ?
View SolutionIf →A×→B=→C+→D, them select the correct alternative:
View Solution
