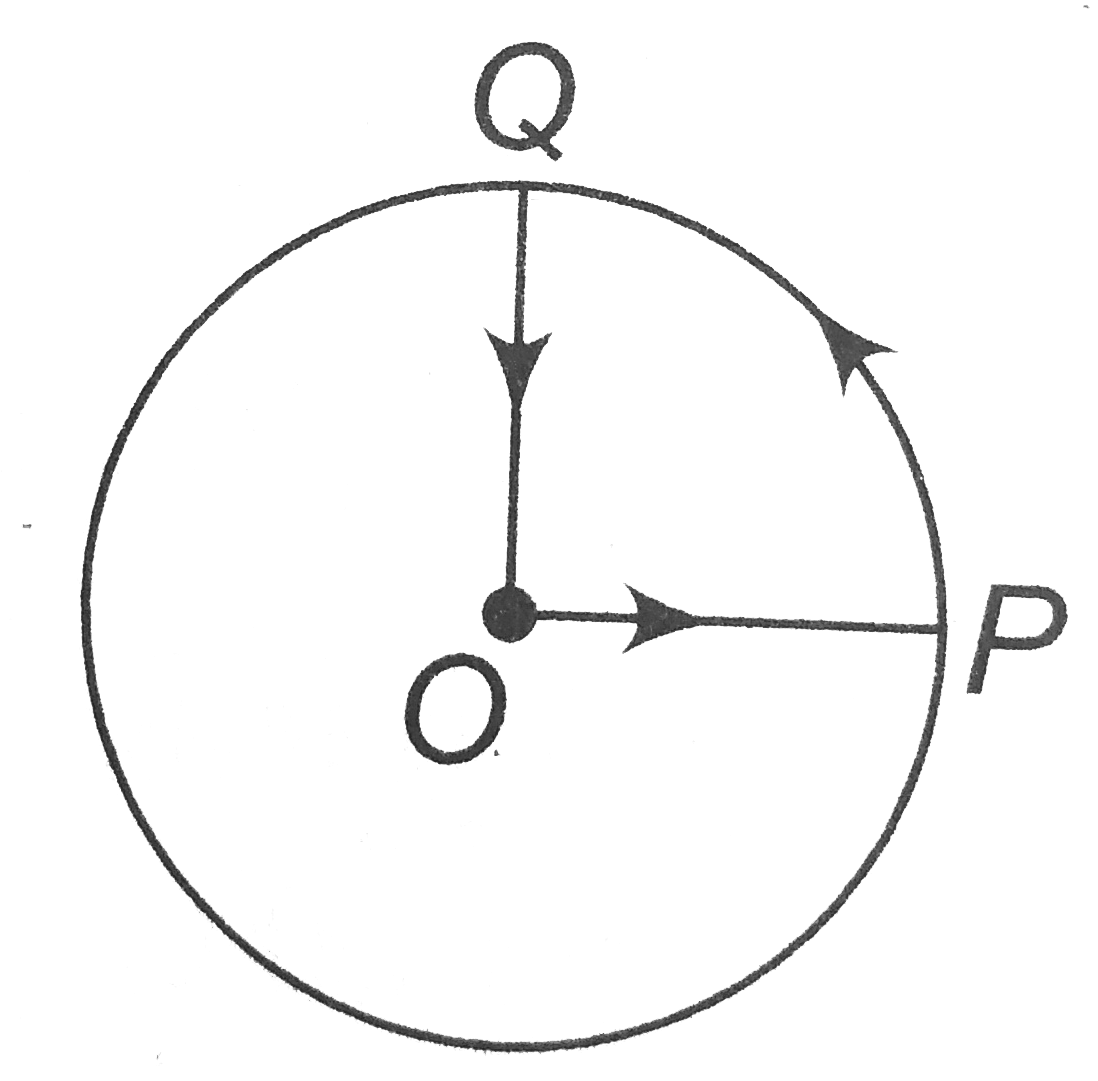
A cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ circumference and returns to the centre along OQ as shown in fig. If the round trip taken ten minutes, the net displacement and average speed of the cyclist (in kilometer per hour) is
0.1
π+42,0
21.4,π+42
0, 21.4
The correct Answer is:D
Since the initial position coincides with the final position. So, net displancement of the cyclist =zero
Aveerage speed of the cyclist=Total distance travelledTotal time taken
=OP+PQ+QO10kmmin−1=1+π2×1+110kmmin−1
=π+420kmmin−1=π+420×60kmh−1=21.4kmh−1
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Miscellaneous Questions14videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Higher Order Thinking Skills8videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Projectile Motion29videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason15videos
MOTION IN A STRAIGHT LINE
Similar Questions
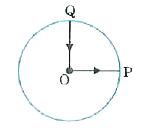
A cyclist starts from the centre O of a circular park of radius 1km , reaches the edge P of the park , then cycles along the circumference and returns to the centre along QO as shown in figure . If the round trip takes 10 min. what is the (a) net displacement . (b) average velocity and (c) average speed of the cyclist ?
 View Solution
View SolutionA cyclist travels from centre O of a circular park of radius 1 km and reaches point P. After cycling along 1/4 th of the circumference along PQ, he returns to the centre of the park along QO. If the total time taken is 10 minutes, calculate (i) net displacement (ii) average velocity and (ii) average speed of the cyclist.
View Solution
Knowledge Check
- Question 1 - Select One
A cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ cicumference and returns to the centre along OQ as shown in fig. If the round trip taken ten minute, the net displacement and average speed of the cylists (in kilometer and kinetic per hour) is
 A0,2(π+4)Bπ+42,0C21.4,π+42D0,3(π+4)
A0,2(π+4)Bπ+42,0C21.4,π+42D0,3(π+4) - Question 2 - Select One
A cyclist starts from the centre O of circular path of radius 10 m, covers the radius of circular path and reaches at point X on circumference, then cycles along the semi-circular path and reaches the point Y. If he takes 10 minutes to go from O to Y via X, then the net displacement and average speed of the cyclist would be
AZero,10ms−1B10m,(1+π60)ms−1C10m,(1+π6)ms−1D10m,(1−π60)ms−1 - Question 3 - Select One
A cyclist rides along the circular path of a circular horizontal plane of radius R, the firctional coefficient being dependent only on distance r from the centre O of the plane as μ=μ0(1−rR), where μ0 is a constant.
Find the radius of the circle such that the cyclist can ride with the maximum velocity.ARBR2CR3DR4
A cyclist starts form centre O of a circular park of radius 1km and moves along the path OPRQO as shown Fig. 2 (EP).15. If he maintains constant speed of 10ms−1, what is his acceleration at point (R )in magnitude and direction ?
 . View Solution
. View SolutionA cyclist starts form centre O of a circular park oa radius 1km and moves along the path OPRQO as whown Fig. 2 (EP).15. If he maintais constant speed of 10ms−1, what is his acceleration at point (R )in magnitude and direction ?
 . View Solution
. View SolutionThere is a circular park of radius 24 m and there is a pole at a distance of 26 m from the centre of the park os shown in the figure. It is planned to enclose the park by planting trees along line segments PO and PR tangential to the park.
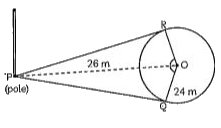
Find the length of PQ and PR.View SolutionA cyclist rides along the circumference of a circular horizontal plane of radius R, with the friction coefficient μ=μ0(1−rR), where μ0 is constant and r is distance from centre of plane O. Find the radius of the circle along which the cyclist can ride with the maximum velocity, what is this valocity?
 View Solution
View SolutionDurga walks 5 km from her home to school in 60 minutes, then bicycles back to home along the same route at 15 km per hour. Her sister Smriti makes the same round trip, but does so at half of Durga's average speed. How much time does Smirti spend on her round trip ?
View Solution

