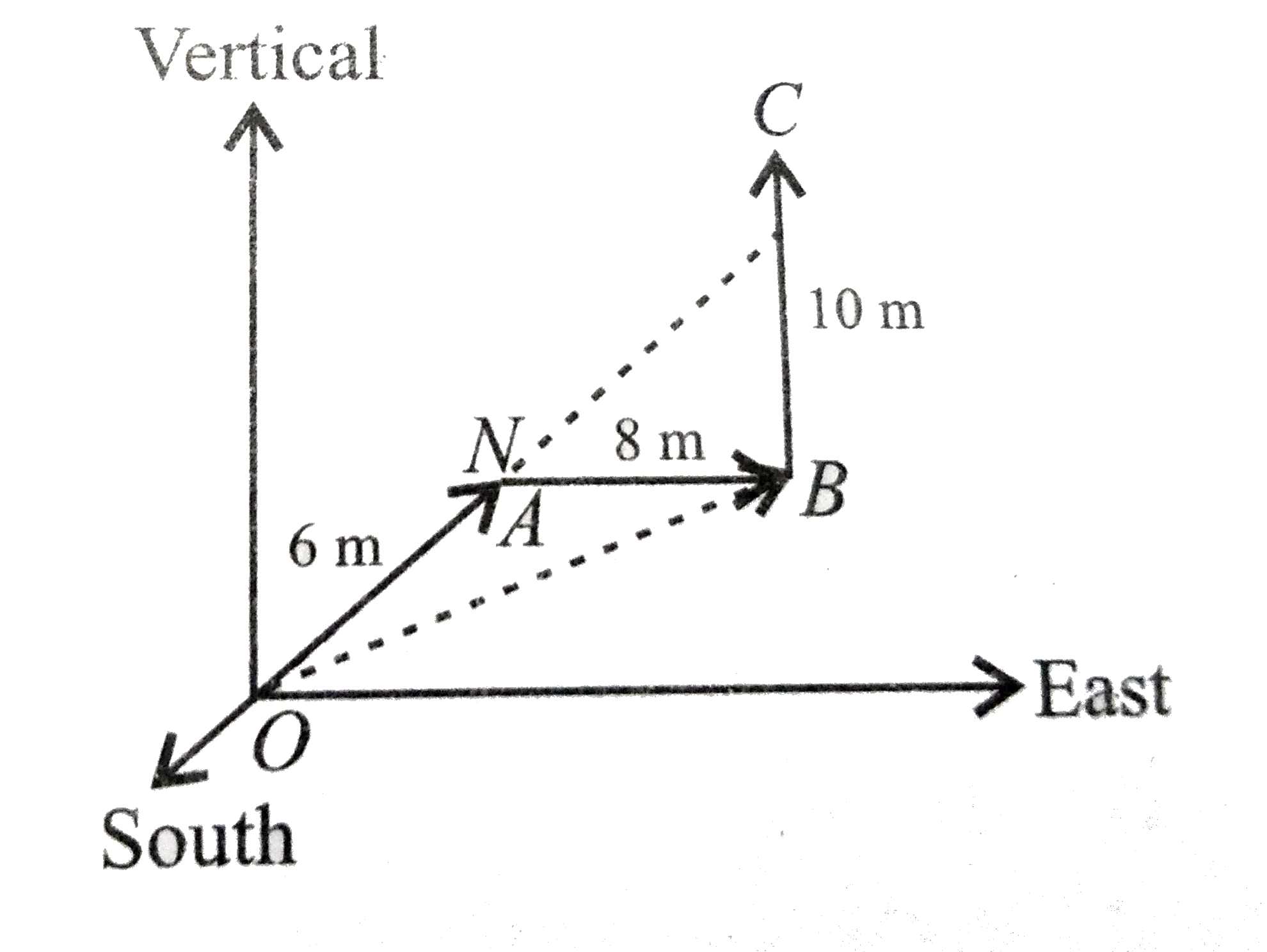
A body moves 6m north, 8m east and 10m vertically upwards, what is its resultant displacement from initial position

A

$10 \sqrt{2} m$

B

$10 m$

C

$\frac{10}{\sqrt{2}} m$

D

$20 m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The situation is as shown in the figure
$O C = \sqrt{A O^{2} + A B^{2} + B C^{2}}$
$= \sqrt{6^{2} + 8^{2} + 10^{2}} = 10 \sqrt{2} m$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Higher Order Thinking Skills
8videos
MOTION IN A PLANE
BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - NCERT Exemplar
10videos
MOTION IN A PLANE
BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Uniform Circular Motion
14videos
MOTION IN A PLANE
BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15videos
MECHANICAL PROPERTIES OF SOLIDS
BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15videos
MOTION IN A STRAIGHT LINE

Similar Questions

Knowledge Check

Question 1 - Select One
A particle moves $3 m$ north, then $4 m$ east, and then $12 m$ vertically upwards, its displacement is
A $12 m$
B $13 m$
C $19 m$
D $15 m$
Question 2 - Select One
A particle has a displacement of 12 m towards east then 5 m forwards north and then 6 m vertically upwards the resultant displacement is nearly
A10.4m
B12.19m
C14.32m
D13.06m
Question 3 - Select One
A person goes 10 km north and 20 km east. What will be the displacement from initial point?
A22.36 km
B2 km
C5 km
D20 km

NCERT FINGERTIPS-MOTION IN A PLANE -Miscellaneous Questions

Home
Ask Doubt
Profile