The ratio of charge to mass of an electron in coulombs per gram was determined by J.J. Thomson. He determined this ratio by measuring the deflection of cathode rays in electric and magnetic fields. What value did he find for this ratio?
−1.76×108 coulombs/g
1.76×10−8 coulombs/g
−1.76×1010 coulombs/g
−1.76×10−10 coulombs/g
The correct Answer is:A
Topper's Solved these Questions
- STRUCTURE OF ATOM BOOK - NCERT FINGERTIPSCHAPTER - STRUCTURE OF ATOM EXERCISE - Atomic Models
5 Videos
- STRUCTURE OF ATOM BOOK - NCERT FINGERTIPSCHAPTER - STRUCTURE OF ATOM EXERCISE - Developments Leading To The Bohr'S Model Of Atom
14 Videos
- STATES OF MATTER BOOK - NCERT FINGERTIPSCHAPTER - STATES OF MATTER EXERCISE - Assertion And Reason
15 Videos
- THE P-BLOCK ELEMENTSBOOK - NCERT FINGERTIPSCHAPTER - THE P-BLOCK ELEMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
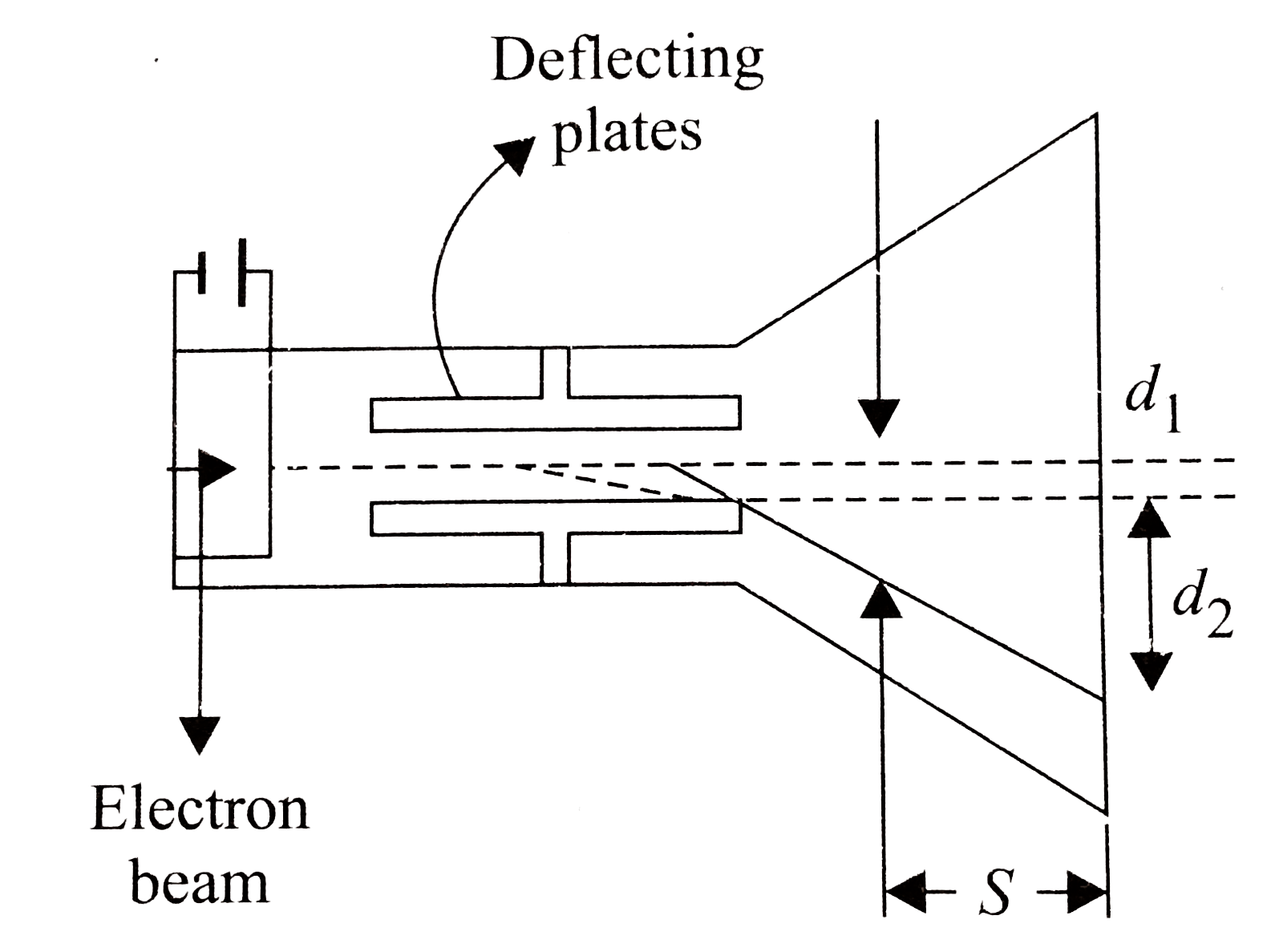
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experiment
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
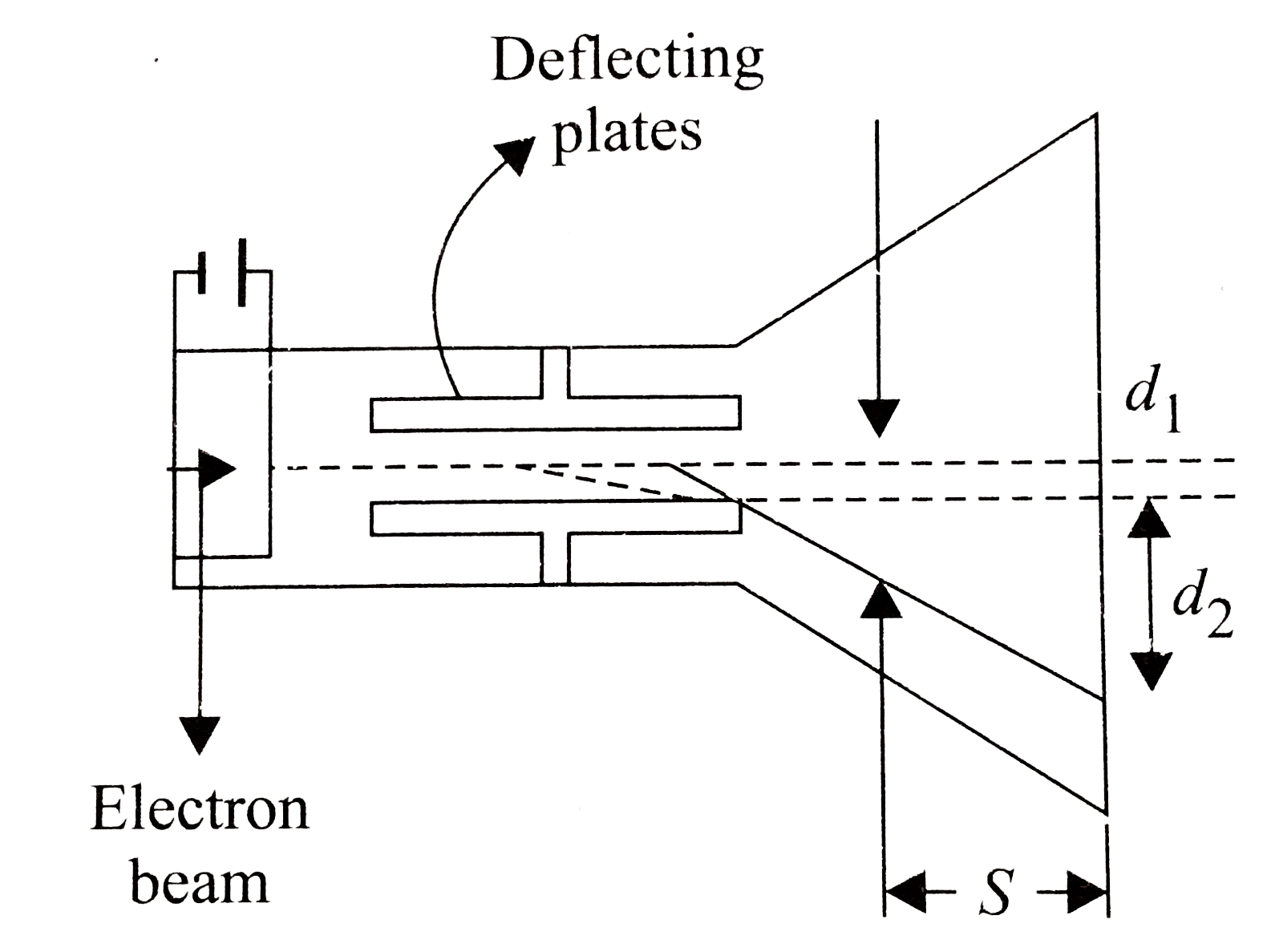
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
View Solution
Knowledge Check
Charge to mass ratio of electron was determined by
AJames ChadwickBJ.J. ThomsonCGoldsteinDErnest RutherfordFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.

Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experimentAThe electric field point to the top, while the magnetic field point into the pageBThe electric field point to the top, while the magnetic field point out of pageCElectric field points to the bottom, while the magnetic field point out of pateDElectric field points to the bottom, while the magnetic field points into the pageFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.

Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron isA1.5×1011Ckg−1B2×1011Ckg−1C2.5×1011Ckg−1D3×1011Ckg−1
If He+ ion undergoes transition n=2 → 1 the ratio of final to initial magnetic field due to motion of electron at the nucleus will
View SolutionIn an experiment to determine e/m using Thomson's method, electrons from the cathode accelerate through a potential difference of 1.5 kV. The collimated beam of electrons is made to enter a region of crossed electric and magnetic fields, both perpendicular to beam direction. Two parallel plates 2.0 cm apart held at a potential difference of 400 V provide the electric field. while a magnetic field of 8.6×10−4T is produced by Helmholtz coils arrangement. The beam hits the fluorescent screen at the end of the tube undeflected. Determine the charge to mass ratio of electron.
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
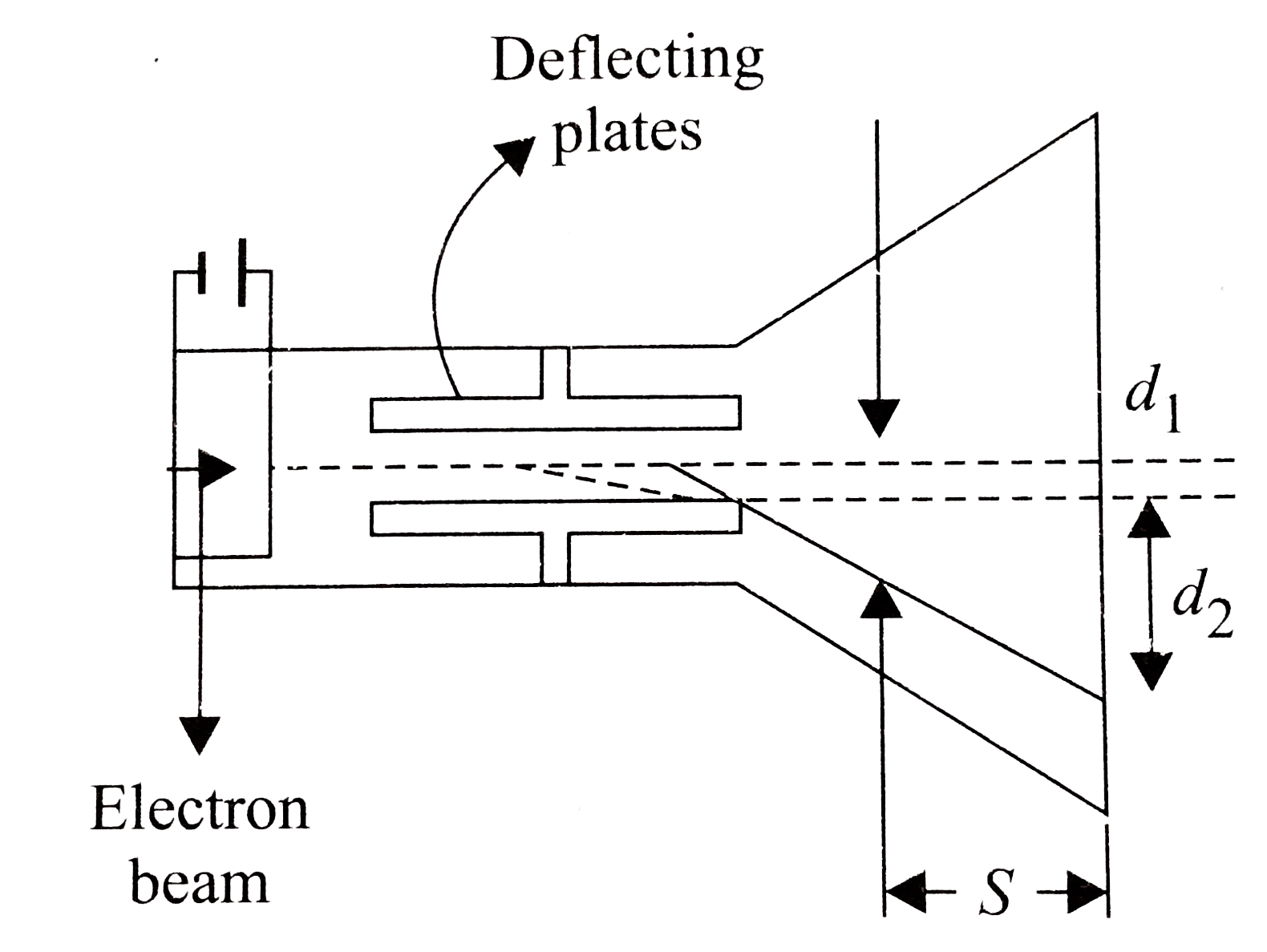
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron speed were doubled by increasing the potential differece V, which of the following would be true in order to correctly measure e/m
View SolutionWhich of the following are the properties of an electron?
1. Electron is a constituent of cathode ray
2. Electron is a nagatively charged particle
3. The mass of the electron is equal to the mass of the proton
4. Electron is deflected by tyhe electric field but not by magnetic field
Select the correct answer using the code given below:
View SolutionIf He+ ion undergoes transition n=2 → 1 the ratio of final to initial magnetic field due to motion of electron at the nucleus will
View Solution
