The six faces of a die are marked [A],[B],[C],[D],[O],[F]. The event M is getting a vowel on the upper face of the die when it is rolled. Complete the following activity and find the probability of the event :
S={□},n(S)=□
M={□},n(M)=□
P(M)=n(M)n(S)=□□=□
The correct Answer is:S={A,B,C,D,E,O}n(S)=6.
M={A,E,O},n(M)=3.
P(M)=36=12.
Step by step video, text & image solution for The six faces of a die are marked [A],[B],[C],[D],[O],[F]. The event M is getting a vowel on the upper face of the die when it is rolled. Complete the following activity and find the probability of the event : S={square},n(S)=square M={square},n(M)=square P(M)=(n(M))/(n(S))=(square)/(square)=square by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
The six faces of a die are marked as shown below: A,B,C,D,E,O.
The event M is getting a vowel on the upper face of the die when it is rolled. Compete the following activity to find the probability of the event.
 View Solution
View SolutionIn the following A.P. 's find the missing terms in the boxes :
−4,□,□,□,□,6View SolutionIn the following A.P. 's find the missing terms in the boxes :
□,38,□,□,□,−22View SolutionThe following table shows the blood groups of employees in a bank. Event C is the blood group of an employee is AB.
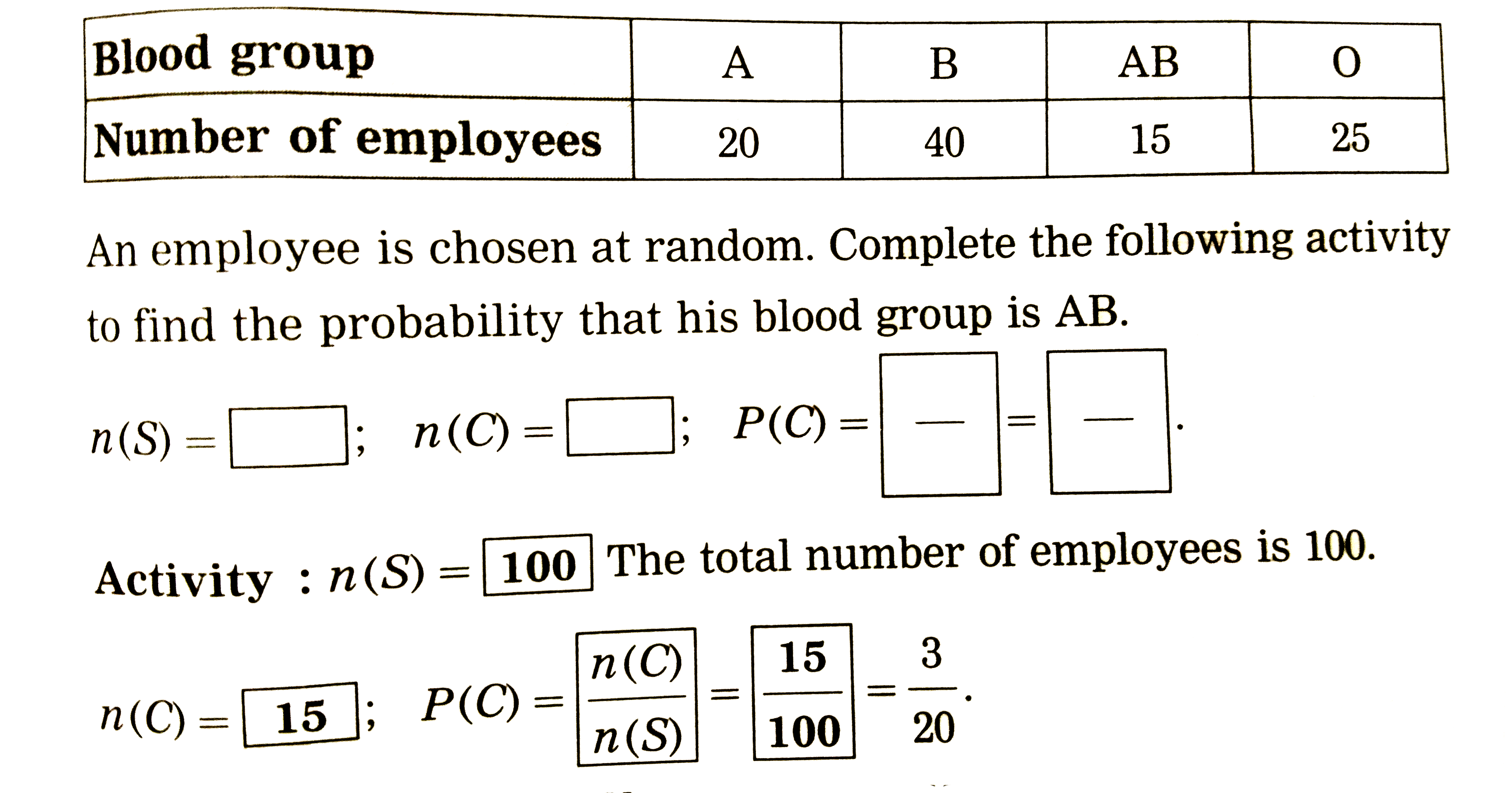
An employee is chosen at random. Complete the following activity to find the probability that his bond group is AB.
n(S)=□n(C)=□,P(C)=≡−.View SolutionThe faces of a die bear the numbers 1,3,5,7,9,11. The die is rolled. Find the probability of getting a perfect square number on the upper face of the dice.
(i)S={1,3,5,7,9,11} (ii)∴n(S)=6
(iii) Let A be the event of getting a perfect square number. Then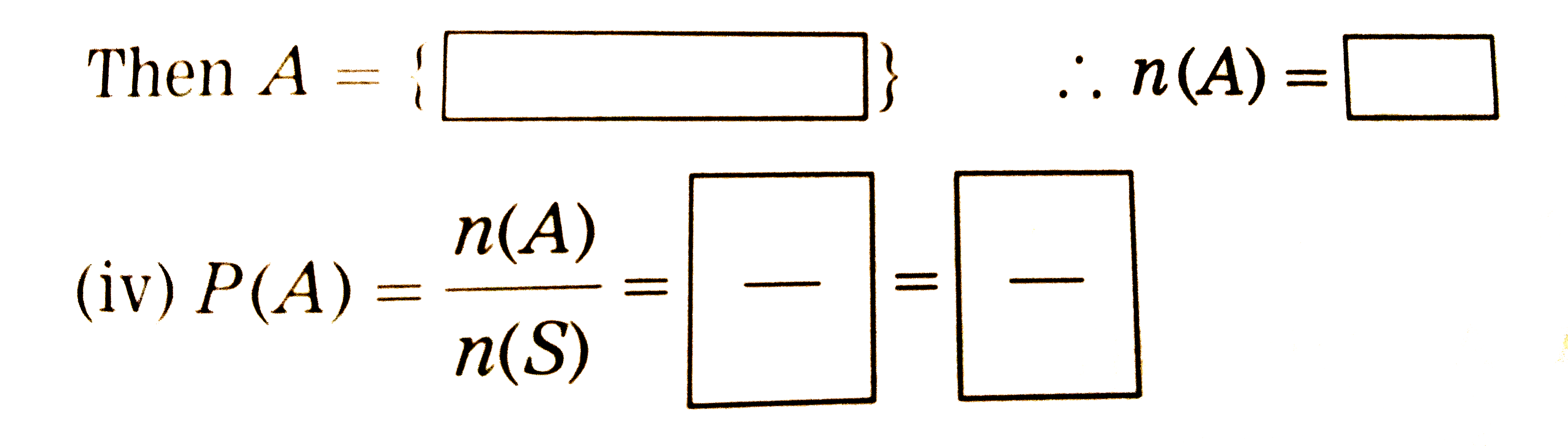
P(A)=n(A)n(S)=−=−View SolutionA die is thrown, then find the probability of the following events, A is an Event: getting an odd number on the upper surface of the die. B is an Event getting a perfect square on the upper surface of the die.
View SolutionComplete the following reactions :
Cl2(g)+H2O(l)→□+□
Zn(s)+2HCl(aq)→□+□
CuSO4(aq)+Fe(s)→□+□View SolutionThe first term and the common difference of an A.P. are 10 and 5 respectively. Complete the following activity to find the sum of the first 30 terms of the A.P.
Sn=n2[□+(n−1)d]
∴S30=302[20+(30−1)×□]
=15[20+□]
=15×165
=□View SolutionIf one die is rolled then find the probability of each of the following events
Getting a number which is less than 7 on the upper face.View SolutionThe perimeter of the square is 64m. then the side of the square is:
View Solution

