Six faces of a die are shown below :
A,B,C,D,E,A
If the die is rolled oncen find the probability that
The correct Answer is:A, B, C
The die is rolled once.
S={A,B,C,D,E,A} ∴n(S)=6
(1) Let 'A' appear on the upper face
ThenA={A,A} ∴n(A)=2
P(A)=n(A)n(S)=26=13
(2) Let 'D' appear on the upper face.
ThenD={D} ∴n(D)=1
P(D)=n(D)n(S)=16.
Similar Questions
Six faces of a die are as shown below
If the die is rolled once, find the probability of
i. 'A' appears on upper face.
ii. 'D' appears on upper face.
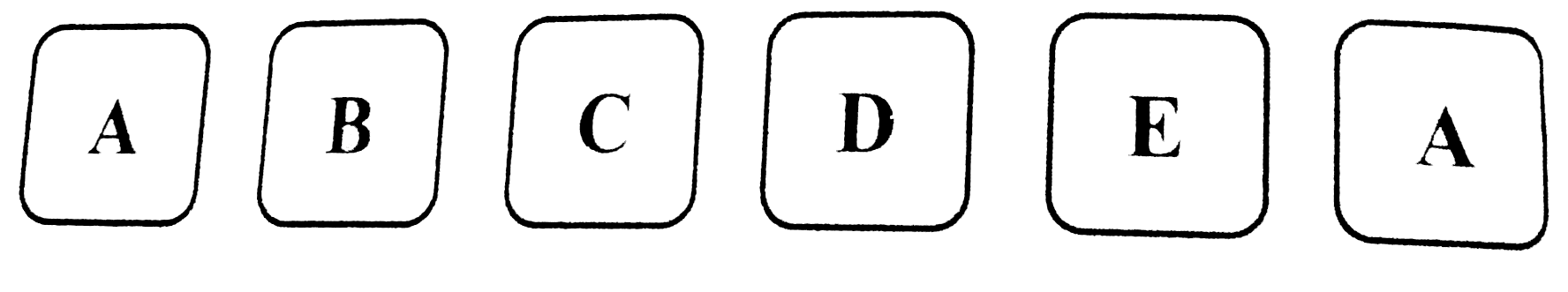
View SolutionThe faces of a die bear number 0,1,2,3,4,5.
If the die is rolled twice, then find the probability that the product of the digits on the upper face is zero.
View Solution
Knowledge Check
Complete the following activity by filling the boxes:
The face of a die bear the numbers 1,3,5,7,9,11.
The die is rolled. Find the probability of getting a perfect square number on the upper face of die.AS=□B∴n(S)=□CLet A be the event of getting a perfect square number.
Then A =□ ∴n(A)=□DP(A)=n(A)n(S)=□□=□A die is rolled. Find the probability of getting a cube number
A536B736C29D16
A die is rolled , Find the probability of getting a 6 .
View SolutionA child has a die whose six faces show the letters as given below:A,B,C,D,E,A.The die is thrown once. What is the probability of getting (i) A? (ii) D?
View SolutionA child has a die whose 6 faces show the letter as given below: A,B,C,A,A,B. The die is thrown once. What is the probability of getting (i) A (ii) B
View SolutionThe six faces of a die are marked as shown below: A,B,C,D,E,O.
The event M is getting a vowel on the upper face of the die when it is rolled. Compete the following activity to find the probability of the event.

View SolutionSix faces of a die are marked with numbers 1,−1,0,−2,2,3 and the die is thrown thrice. The probability that the sum of the numbers thrown is six, is
View SolutionOn a normal standard die one of the 21 dots from any one of the six faces is removed at random with each dot equally likely to the chosen. If the die is then rolled, then find the probability that the odd number appears.
View Solution
