In the following figure AP⊥BC,AD∣∣BC, then find A(ΔABC):A(ΔBCD).
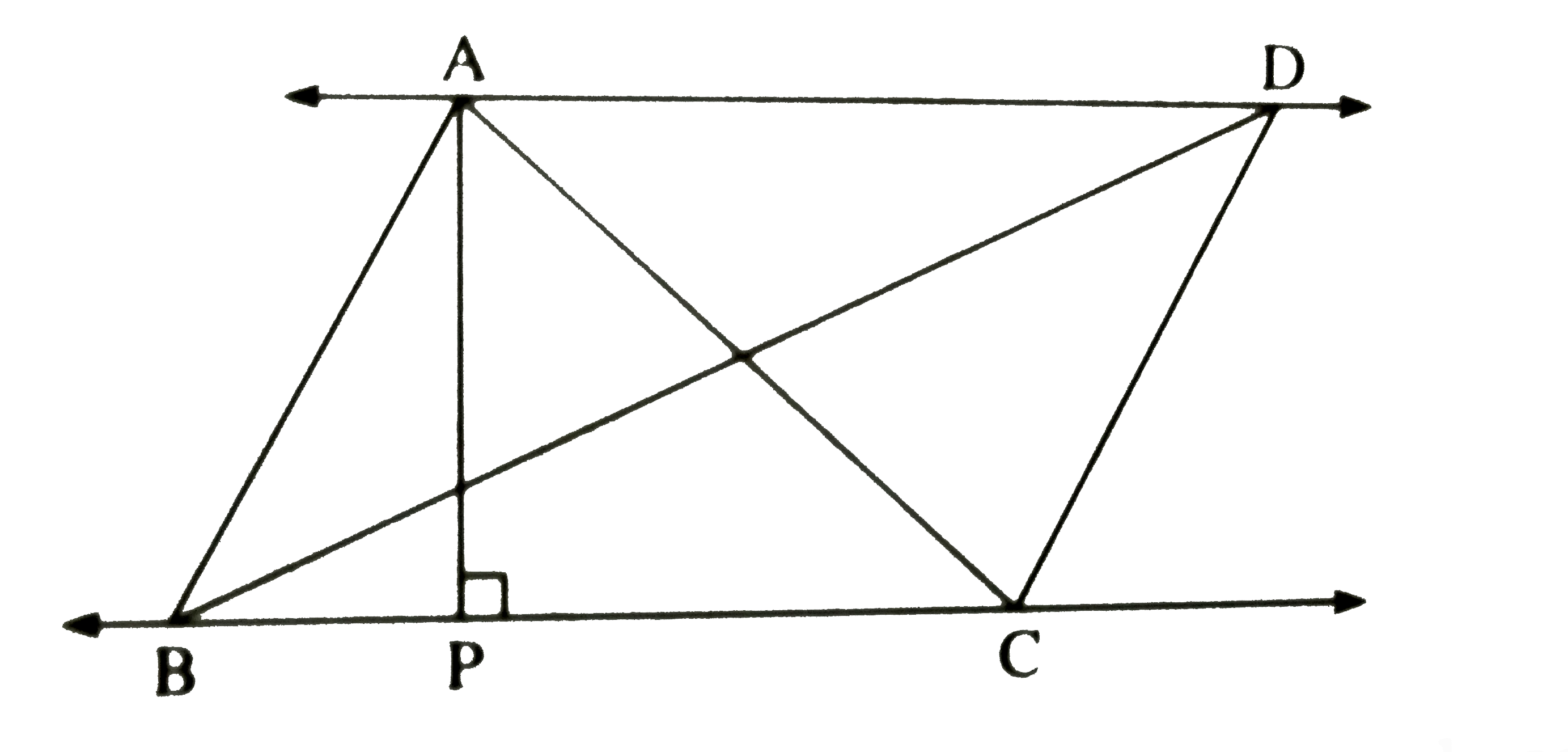
ΔABC and ΔBCD have same base BC. The vertices of ΔABC and ΔBCD lie on the parallel lines AD and BC. The distance between the two parallel lines is the height of the triangles.
Distance between parallel lines is constant.
∴ΔABC and ΔBCD have equal heights.
Areas of two traingles of equal bases and equal heights are equal.
∴A(ΔABC)=A(ΔBCD)
∴A(ΔABC)A(ΔBCD)=11
∴A(ΔABC):A(ΔBCD)=1:1
A(D≤taABC):A(ΔBCD)=1:1
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE15videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)3videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
In the adjoining figure, AP⊥BC ,AD||BC ,then find A(ΔABC):A(ΔBCD) .
View SolutionIn the adjoining figure, AP⊥BC,AD||BC, then find A(ΔABC):A(ΔBCD).
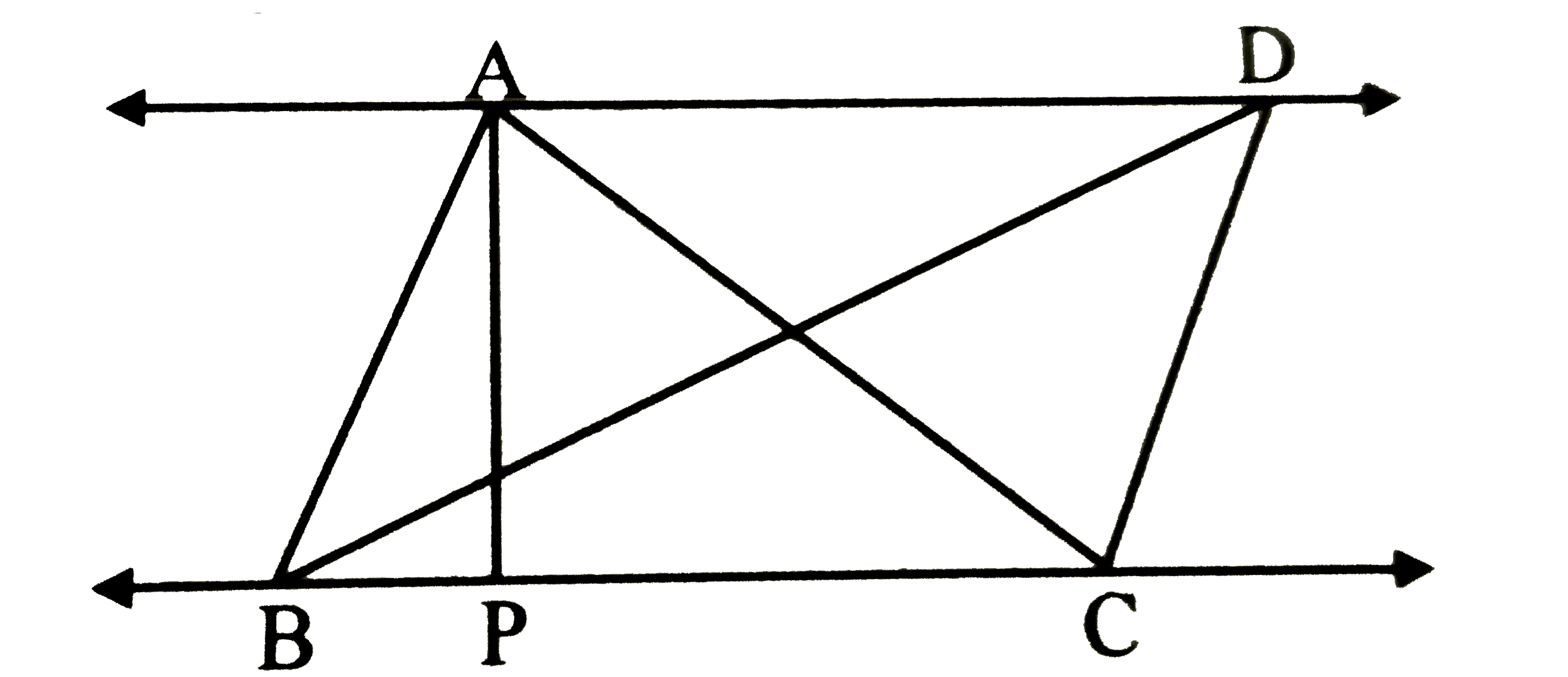 View Solution
View SolutionIn adjoining figure,AP⊥BC , AD∣∣BC ,then find Ar.(ΔABC):Ar.(ΔBCD)Fig.
View SolutionIn the figure BC⊥AB,AD⊥AB,BC=4,AD=8, then find A(ΔABC)A(ΔADB).
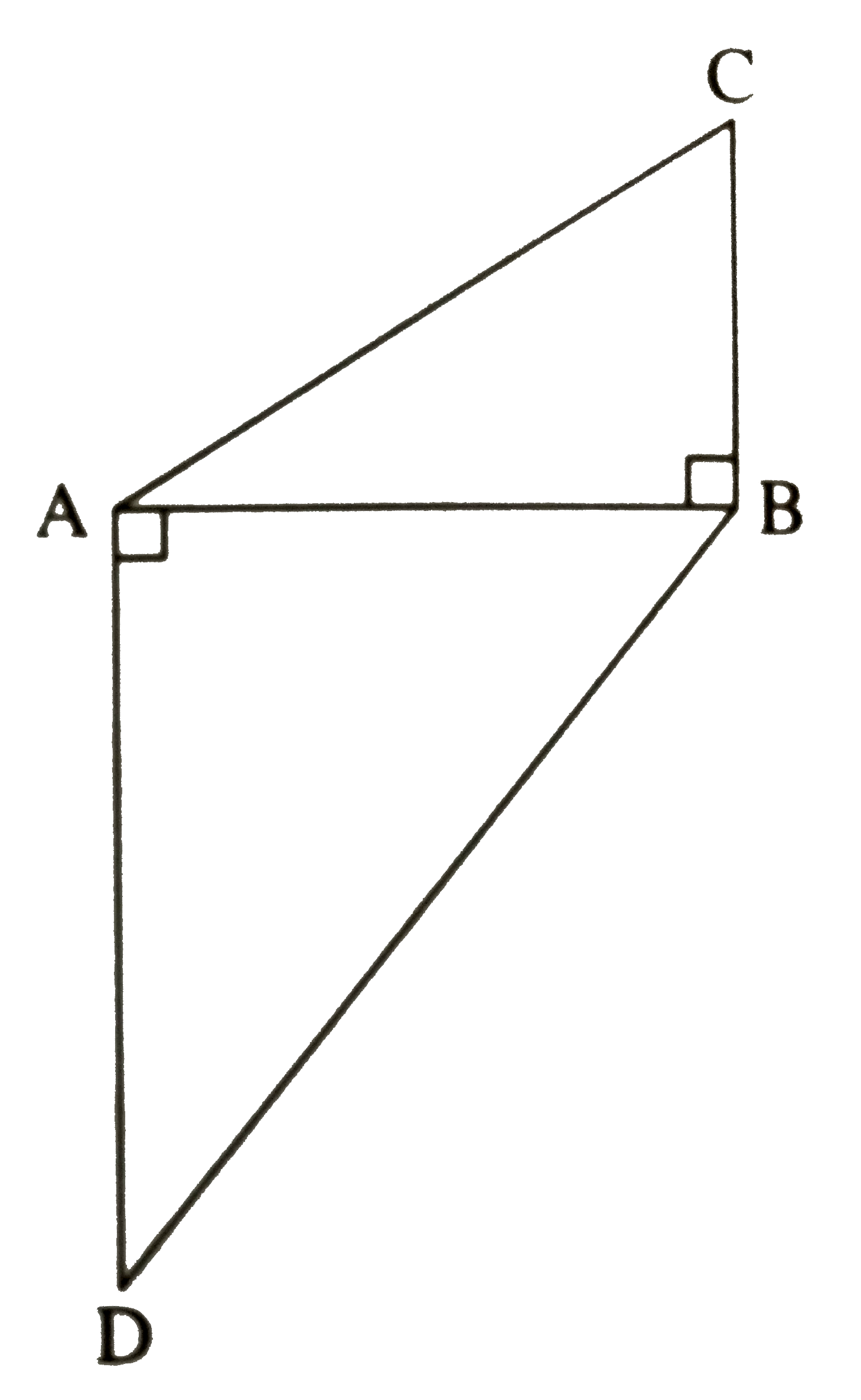 View Solution
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔPBC)A(ΔABC).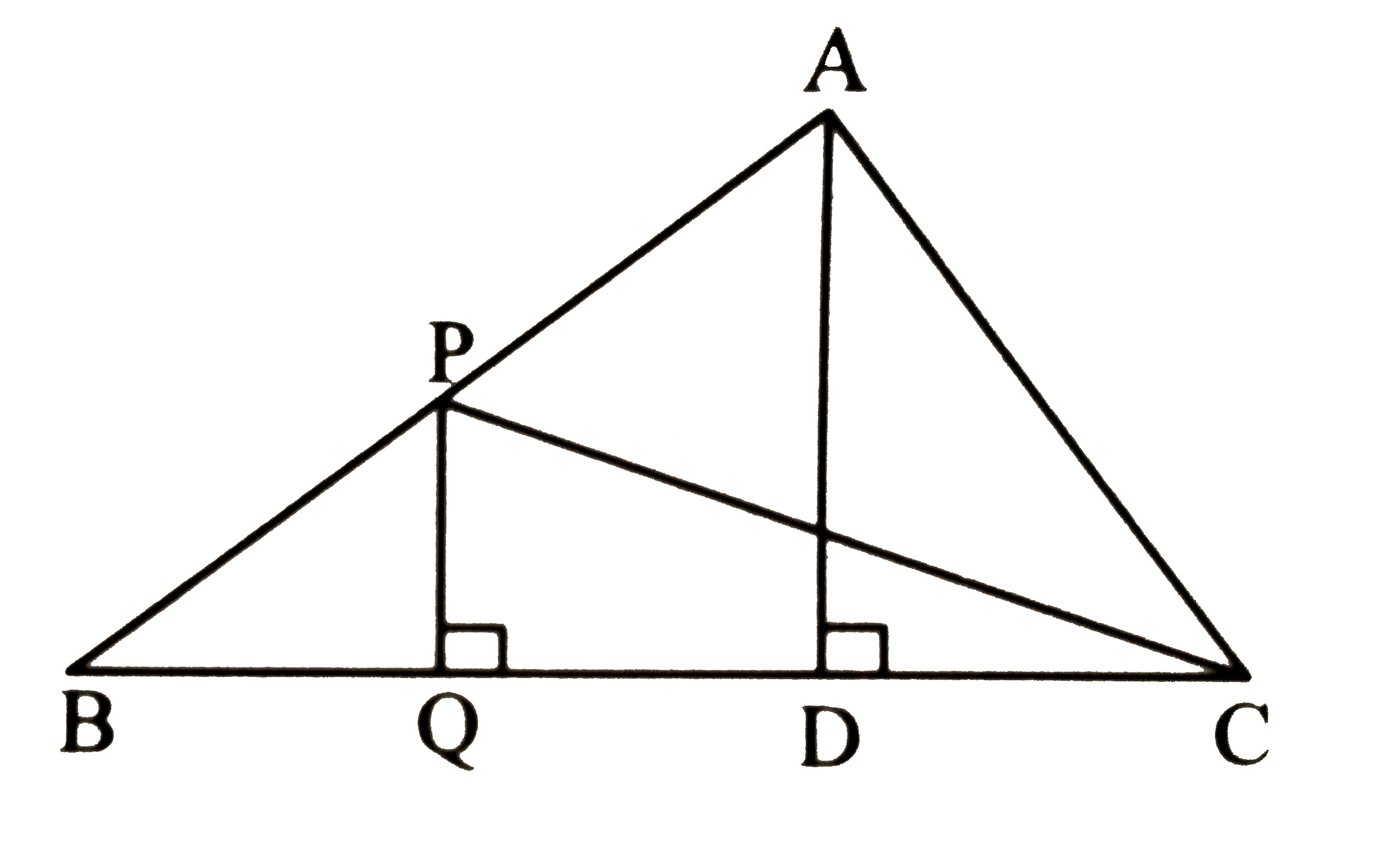 View Solution
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔABC)A(ΔADC).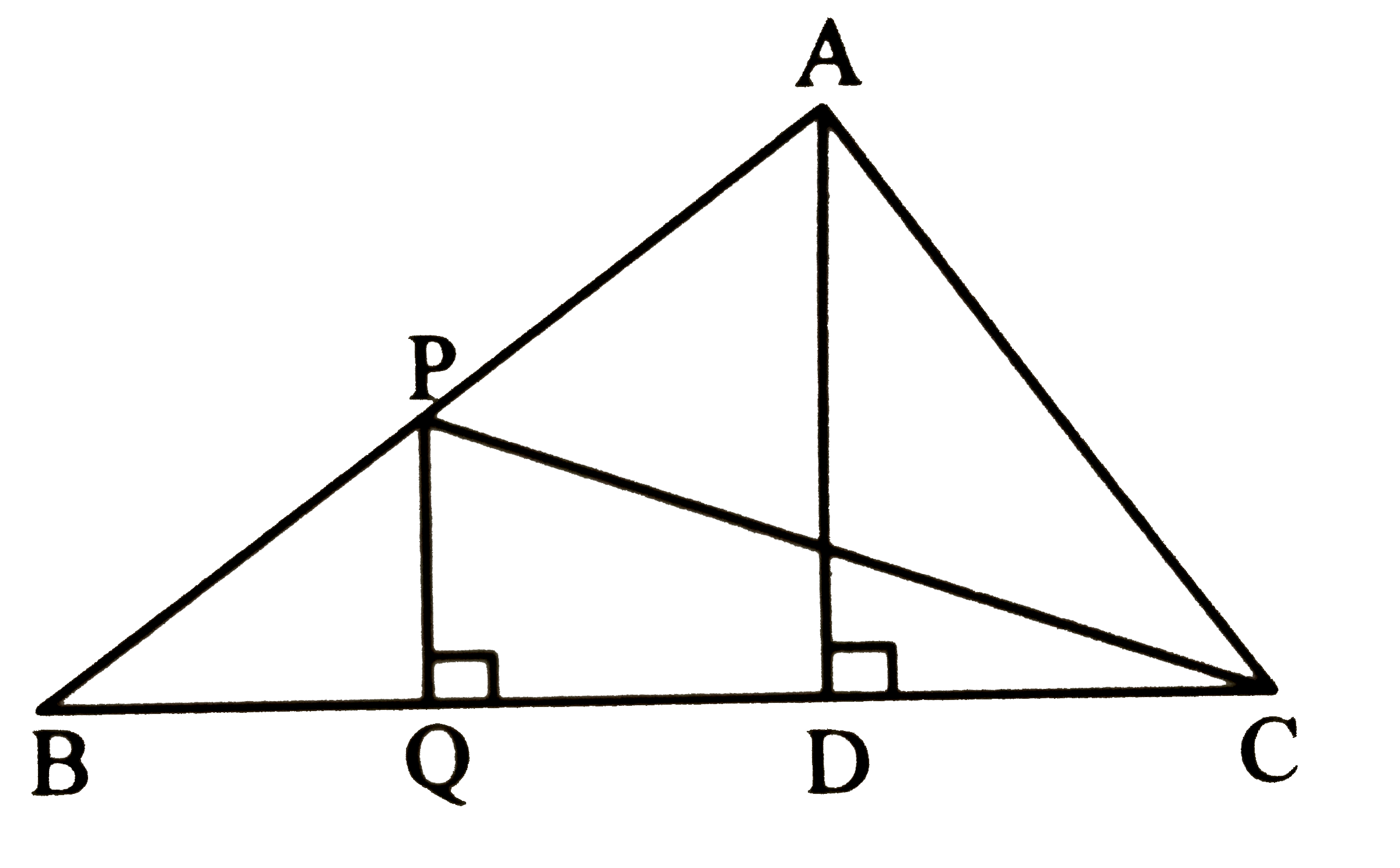 View Solution
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔPQB)A(ΔPBC).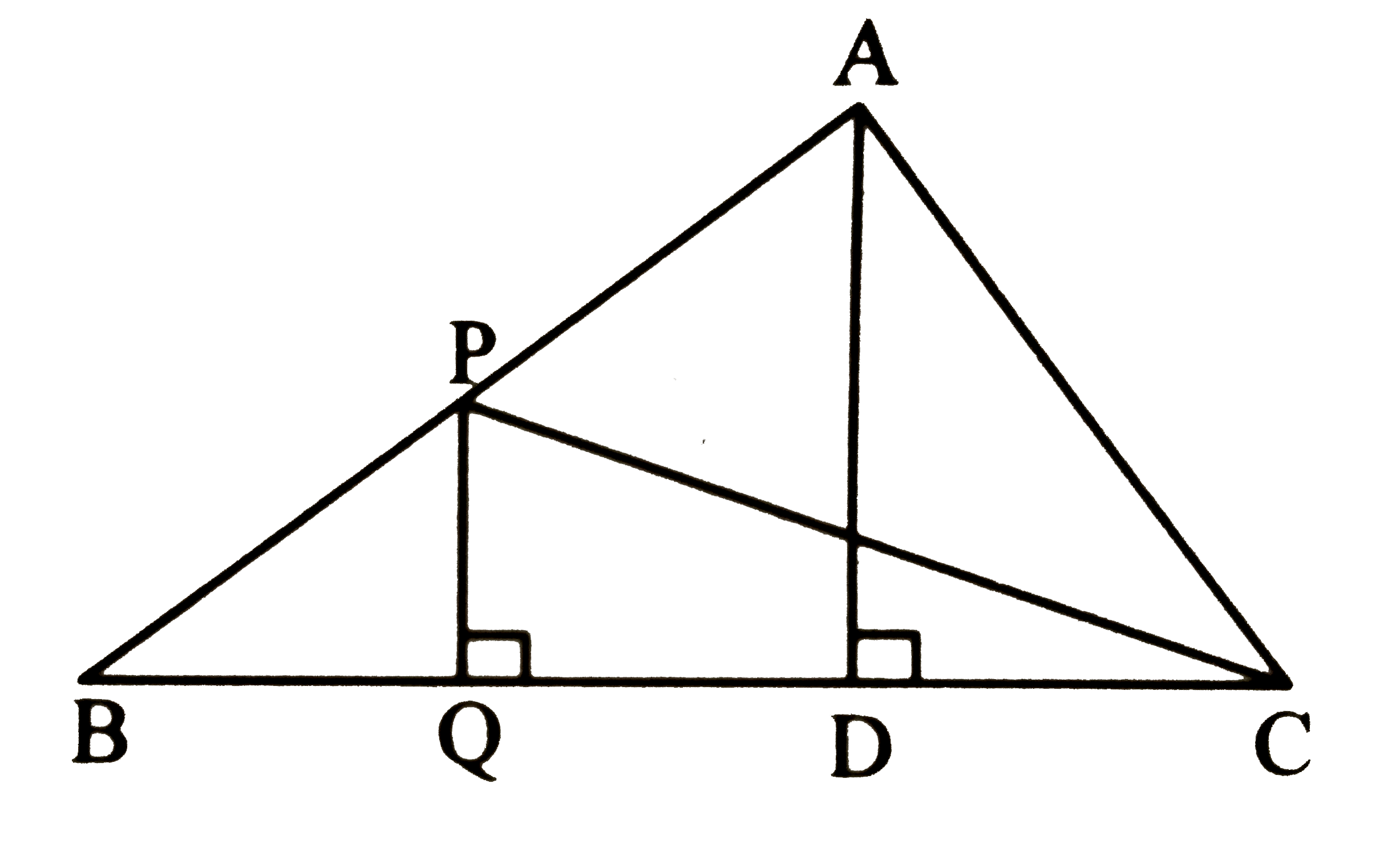 View Solution
View SolutionIn the adjoining figure, PQ⊥BC,AD⊥BC, then find ratio
A(ΔADC)A(ΔPQC)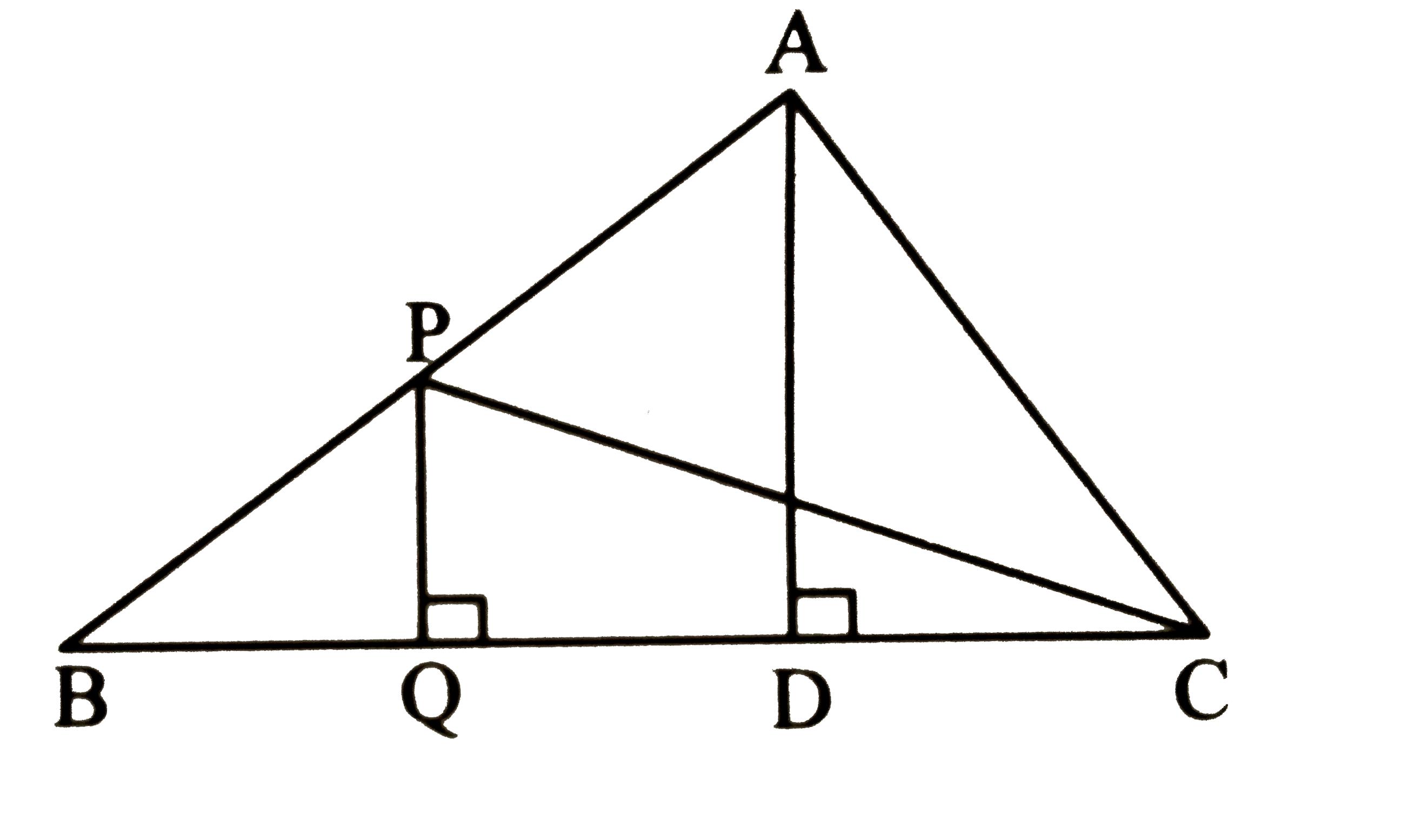 View Solution
View SolutionIn the adjoining figure PQ⊥BC,AD⊥BC, then find following ratios:
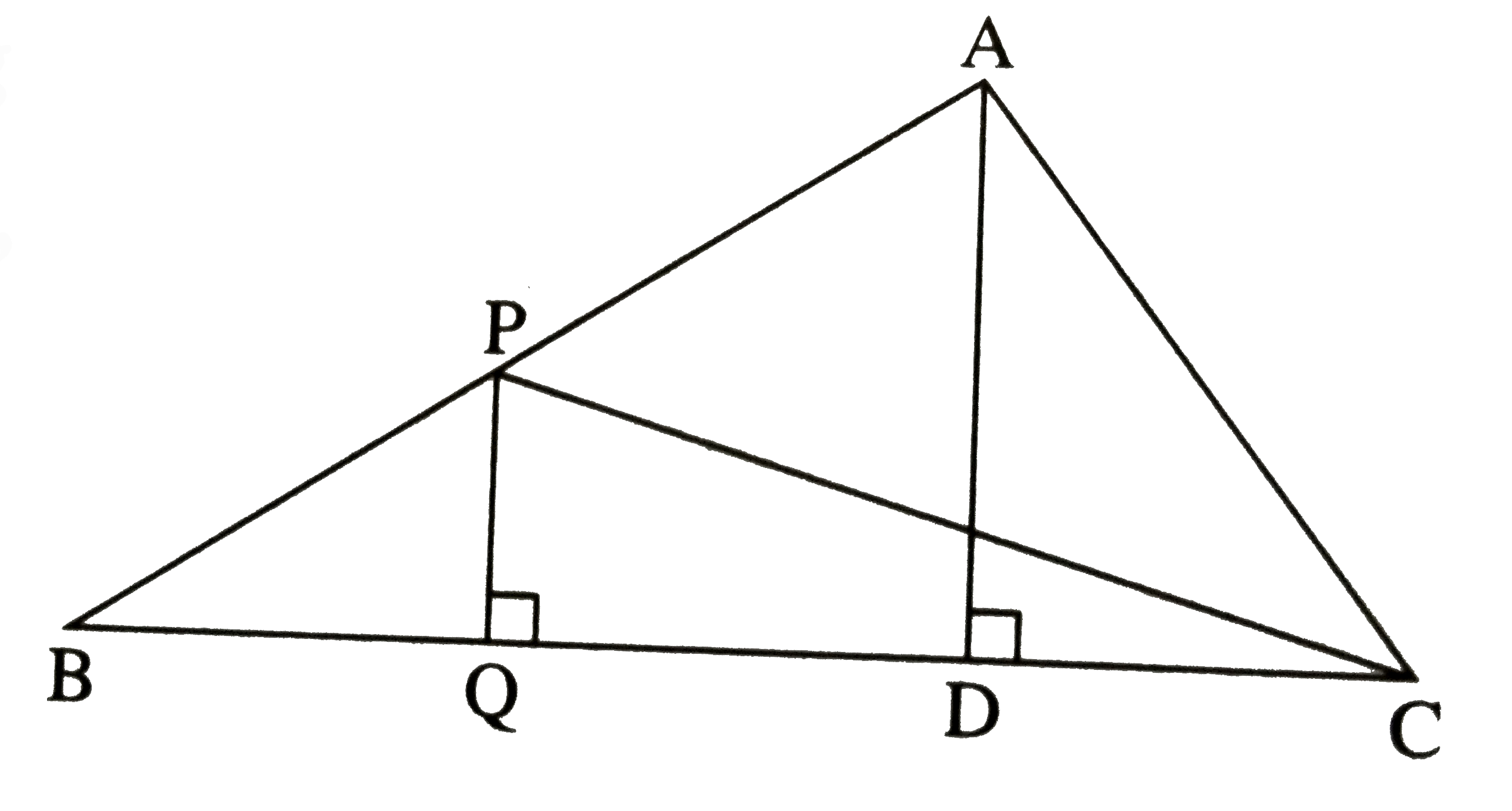
(i( A(ΔPQB)A(ΔPBC) (ii) A(ΔPBC)A(ΔABC)
(iii) A(ΔABC)A(ΔADC)(iv) A(ΔADC)A(ΔPQC)View SolutionIn the given figure if AD||BC, find the value of x.
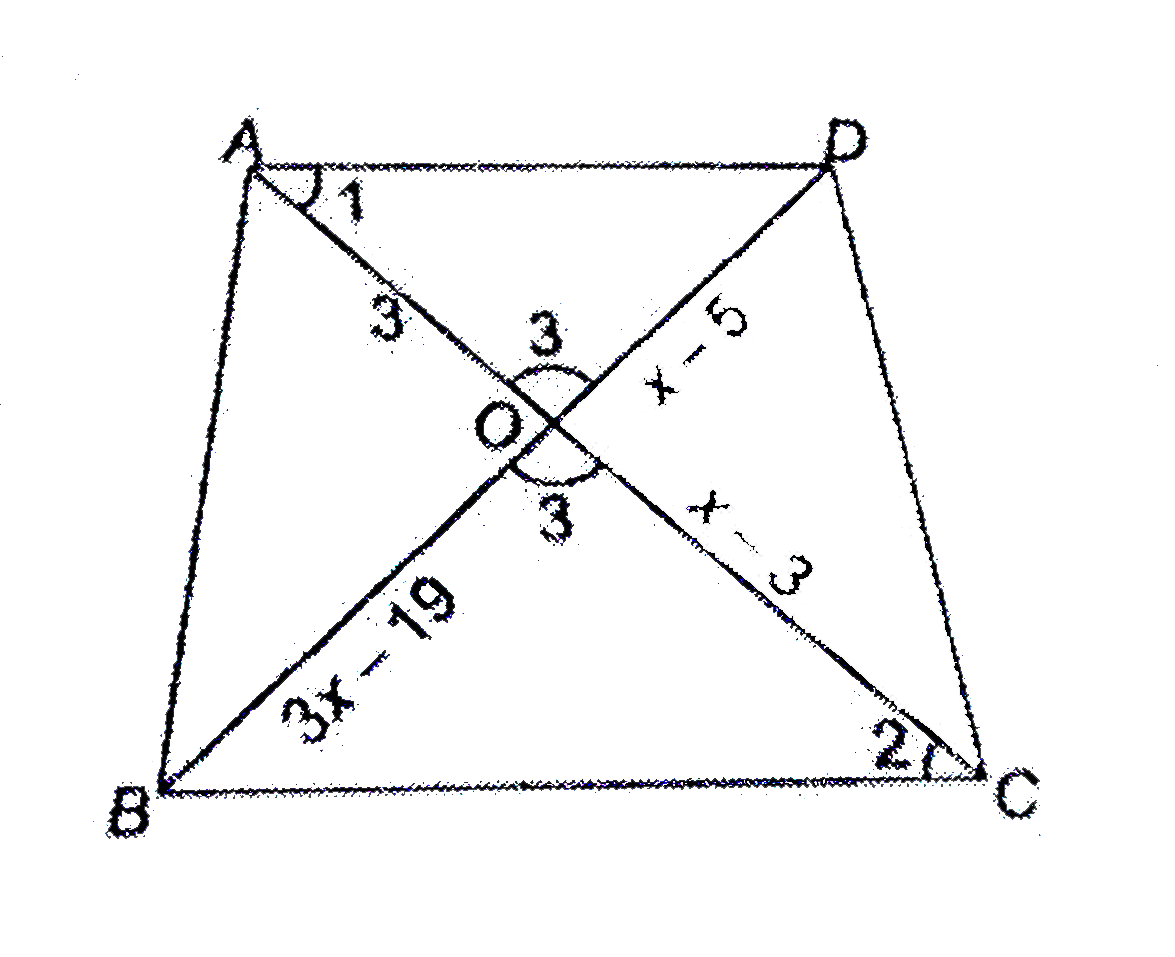 View Solution
View Solution

