If the angle - bisector of two intersecting chords of a circle passes through its centre , then prove that the chords are equal .Solution in Bengali
Let the two chords AB and AC of the circle with centre at O intersect each other at A. The bisector AO of the internal angle ∠BAC passes through the centreO.
We have to prove that AB = AC .
Construction : let us join O, B and O,C .
Proof : In ΔAOB and ΔAOC
∠OBA=∠OAB[∵OB=OA = radii of same circle ]
=∠OCA[∵∠OAB=∠OAC given ]
=∠OCA[∵OC=OA= radii of same circle]
i.e.,∠OBA=∠OCAand∠OAB=∠OAC
and OA is common to both .
By the condition of A - A - S congreucency of congruent triagle .
ΔAOB≅ΔAOC
∴AB=AC[∵ similar sides of congruency triangles].
∴ the chord AB and AC are equal .

Topper's Solved these Questions
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - Example (B. Write true or false )
3 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - Example (C. Fill in the blanks
2 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - Example (Short-Answer Type Questions)
5 Videos
- SPHEREBOOK - CALCUTTA BOOK HOUSECHAPTER - SPHEREEXERCISE - EXERCISE
36 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
Similar Questions
Only one circle can be throught three collinear points .
View SolutionIf the ratio of length of two chords PQ and RS of the circle with centre at O be 1 : 1 then ∠POQ:∠ROS = _________.
View SolutionTwo equal circles of radius 10 cm intersect each other and the length of their common chord is 12 cm . Find the distance between the centre of the circle .
View SolutionIf the volume of a solid hemisphere be 19404 cc, then the radius of the hemisphere will be
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View SolutionTheorem :-2 The perpendicular from centre of a circle to the chord bisects the chord and Perpendicular bisectors of two chords of a circle intersects at the centre.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
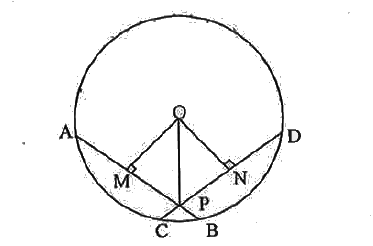
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
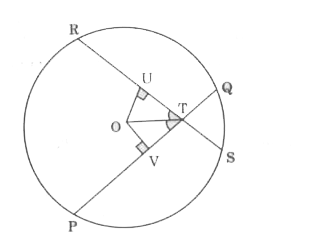
View SolutionIf two intersecting chords of a circle make equal angles with diameter passing through their point of intersection, prove that the chords are equal.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, then Prove chords are equal.
View Solution
