In the adjoining figure, O is the centre of a circle and AB is one of its diameters. The legth of the chrod CD is equal to the radius of the circle. When AC and BD are extended, they intersect each other at a point P. find the value of ∠APBSolution in Bengali
Let us join B.C
Now, AB is a diameter of the circle,
∴∠ACB=90∘[∴ semi-circular angle]
Again in ΔCOD,OC=OD=CD (Given)
∴ΔCOD is an equilateral triangle.
∴ each angle of the triange =60∘∴∠COD=60∘
Now, the central angle produced by teh chord CS is ∠COD and angle in circle is ∠CBD
∴∠COD=2∠CBDor,60∘=2∠CBDor,∠CBD=30∘
∴inΔPBC,∠PCB=90∘[∴ACB=90∘],∠PBC=∠CBD=30∘
∴∠BPC=180∘−(∠PCB+∠PBC)=180∘−(90∘+30∘)=180∘−120∘=60∘
∴∠APB=60∘[∴∠BPC=∠APB]

Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.1 (Very Short-Answer Type Questions) MCQs
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.1 (True or False)
2 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
Area of a circle is 5544square meter ,then calculated the radius of the circle.
View SolutionThe front angle produced by an are of the circle is called the central angle.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View Solutionकिसी वृत्त का केंद्र O है, AB व्यास है और CD चापकर्ण है जोकि OC त्रिज्या के बराबर है। AC और BD को इस प्रकार बढ़ाया जाता है कि वे एक-दूसरे को बिंदु P पर काटते है जोकि वृत्त के बाहर है। ∠APB का माप क्या होगा?
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
View SolutionIn figure, bar(AB) is a diameter of the circle, bar(CD) is a chord equal to the radius of the circle. bar(AC) and bar(BD) when extended intersect at a point E. Prove that angle AEB = 60^@ .
View SolutionIn figure, ¯¯¯¯¯¯AB is a diameter of the circle, ¯¯¯¯¯¯CD is a chord equal to the radius of the circle. ¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD when extended intersect at a point E. Prove that ∠AEB=60∘.
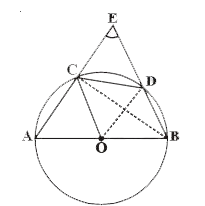
View SolutionIn figure, ¯¯¯¯¯¯AB is a diameter of the circle, ¯¯¯¯¯¯CD is a chord equal to the radius of the circle. ¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD when extended intersect at a point E. Prove that ∠AEB=6∘.
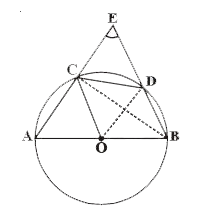
View SolutionIn the given figure, AB is a diameter of the circle, CD is chord equal to the radius of the circle, AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.
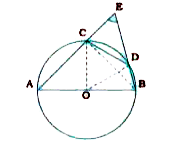
View Solution
