XY is a diameter of a circle. PAQ is a tangent to the circle at the point A lying on the circumference. The perpendicular drawn on the tangent to the circle from X intersects PAQ at Z. Prove that XA is a bisector of ∠YXZ. [GP−X]Solution in Bengali
Let XY be a diameter of the circle with centre at O. PAQ is a tangent to the circel at point A. The perpendicular XZ drawn from X to PAQ intersects PAQ at Z.
To prove : XA is a bisector of ∠YXZ,i.e.,∠YXA=∠ZXA
Construction : Let us join O, A.
Proof : PAQ is a tangent to the circle with centre O at the point A and OA is radius passing through point pf contact A.
∴OA⊥PAQ [by theorem -40]
∴∠OAP=90∘or,∠OAZ=90∘........(1)
Again given that XZ⊥PAQ,∴∠XZA=90∘....(2)
From (1) and (2) we get, XZ∣∣OAandXA is their transversal ∴∠OAX=∠ZXA.....(3)
[∵ alternate angles]
or,∠ZXA=∠AXO[∵OX=OA= radii of same circle]
or∠ZXA=∠YXA
Hence XA is the bisector of ∠YXZ. (Proved)

Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.120videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
01:54View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
03:15View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
02:27View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
03:39View Solutionमाना कि केंद्र बिन्दु O वाले वृत्त पर P और Q दो बिन्दू है । यदि वृत्त के दो बिन्दू P और Q से होकर खींची गई स्पर्श रेखाएं A पर मिलती है, तो ∠PAQ=48∘,then ∠APQ कितना होगा ?
08:30View Solutionदो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते है । A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित है । सिद्ध कीजिए कि BP=BQ है ।
07:17View Solutionदिये गए चित्र में O केन्द्र वाले एक वृत्त के बिन्दु A पर PAQ एक स्पर्शी है तथा ∠BAQ=60∘ तब ∠ABC का मान ज्ञात कीजिए ।
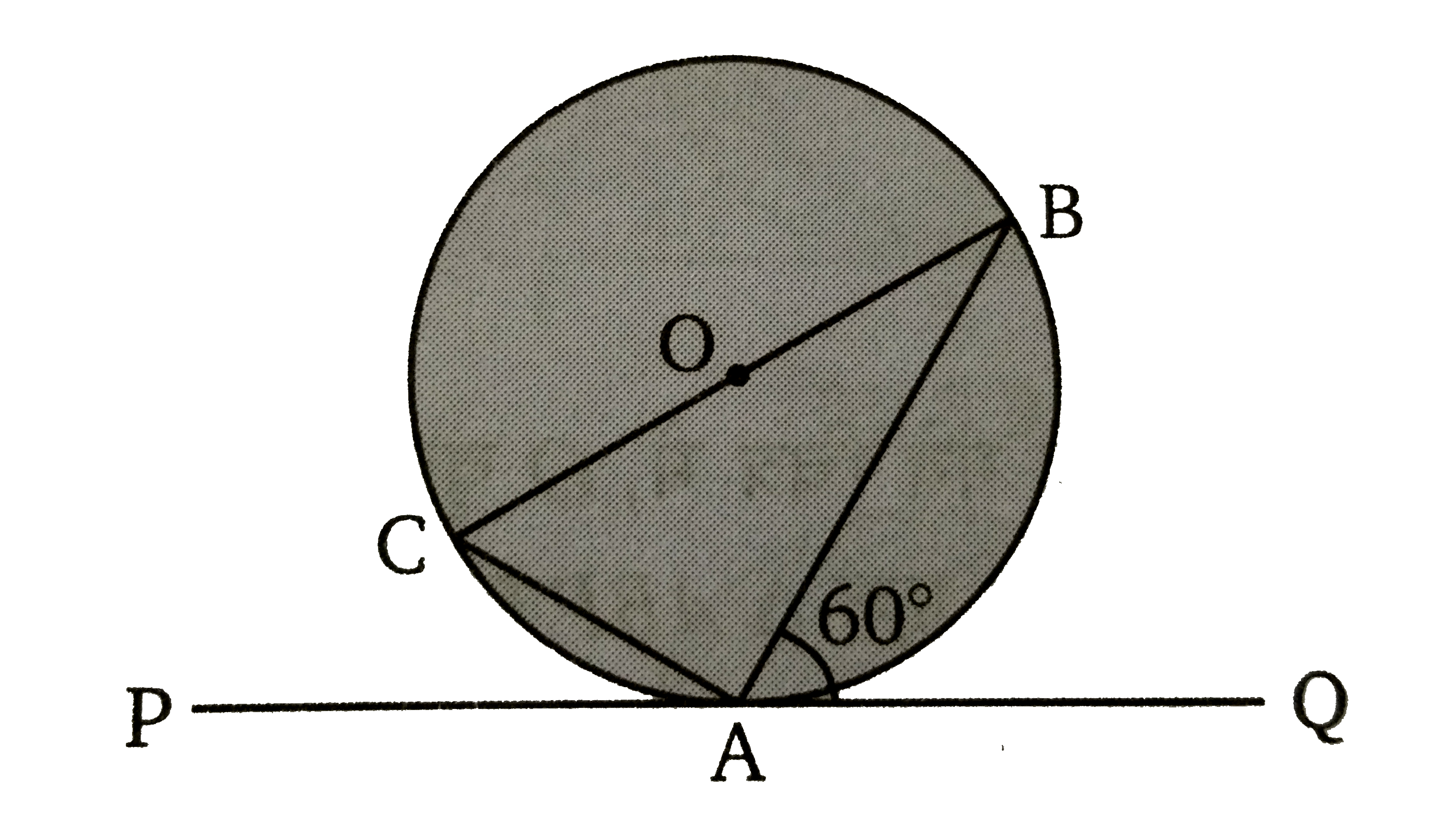 06:21View Solution
06:21View Solutionदिये गए चित्र में, O वृत्त का केन्द्र है। वृत्त के बाहर एक बिन्दु T से वृत्त पर दो स्पर्शी TP व TQ खींची गयी है। यहाँ स्पर्श जीवा वृत्त के शेष भाग से ∠PAQ=70∘ बनाती है। तब दोनों स्पर्शियाँ के बीच का कोण ज्ञात कीजिए ।
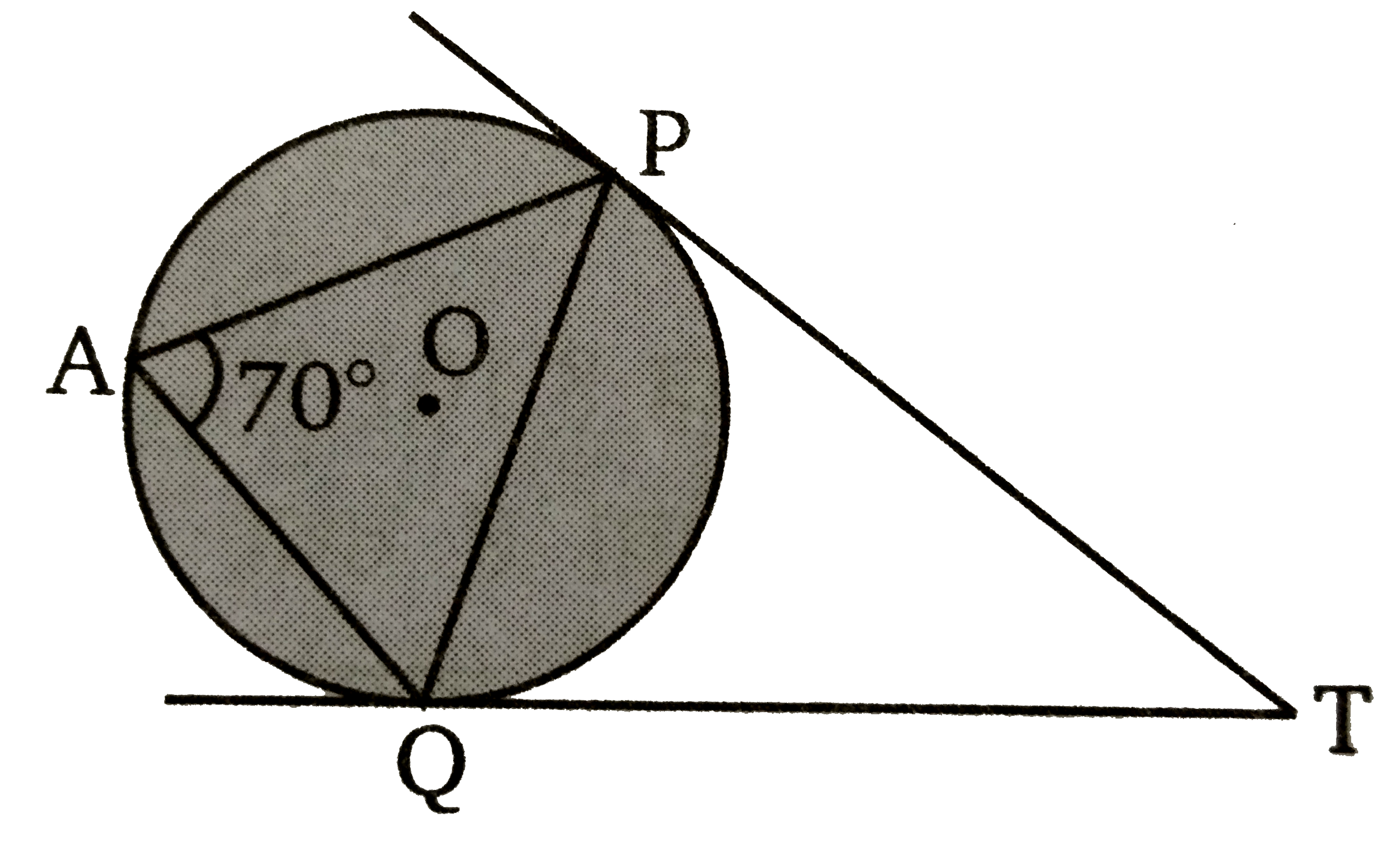 02:40View Solution
02:40View SolutionP is any point on diameter of a circle with centre O.A perpendicular drawn on diameter at the point O intersects the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R.A tangent drawn at the point R intersects extended OP at the point S. Prove theat SP=SR.[GP−X]
02:28View SolutionTwo tangents are drawn from an external point A of the circle with centre at O which touches the circle at the points B and C. Prove that AO is the perpendicular bisector of BC.
03:56View SolutionProve that the internal bisector of the angle between two tangents drawn from an external point of a circle will pass through the centre of the circle.
03:34View SolutionIn the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ=60∘, find ∠ABC :
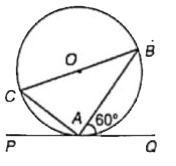 09:10View Solution
09:10View SolutionProve that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
07:07View Solutionপ্রমাণ করো যে, স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব বৃত্তের কেন্দ্রগামী
03:06View SolutionO কেন্দ্রীয় একটি বৃত্ত এঁকেছি যার একটি ব্যাস AB এবং A বিন্দুতে বৃত্তের স্পর্শক PAQ,PAQ-এর সমান্তরাল জ্যা RS,যুক্তি দিয়ে প্রমাণ করো যে AB, RS-এর লম্বসমদ্বিখন্ডক।
04:39View Solution

