The length of radius of a circel with centre O is 5 cm. P is a point at a distacne of 13 cm from the point O. PQ and PR are two tangensts from the point P to the circles, the area of the quadrilaterals PQOR is Solution in Bengali
60 sq-cm
30 sq-cm
120 sq-cm
150 sq-cm
The length of the radius of a circle with centre O.∴OQ=OR=5cm.
P is a point at a distance of 13 cm from the point O.∴OP=13cm
Now, PQ and PR are two tangents from P and OP and OR are radii passing through the point of contact.
∴OQ⊥PQandOR⊥PR
∴∠OQP=90∘and∠ORP=90∘
i.e., ΔPOQandΔPOR are both right-angled triangles.
∴ΔPOQ=12×PQ×OQ[∵PQ= base and OQ = height]
=12×12×5sq−cm.[∵PQ=√OP2−OQ2=√132−52cm
=30sq.cm=√169−25cm=√144cm=12 cm.
Similarly, ΔPOR=12×PR×OR[∵PR= baseand height = OR]
=12×12×5sq−cm[∵PR=PQ=12cm]=30sq−cm.
∴ Ares of the quadrilateral PQOR=ΔPOQ+ΔPOR=30sq−cm+30sq−cm=60sq−cm.
∴ (a) is correct

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View Solution5 cm त्रिज्या तथा O केन्द्र वाले वृत्त से 13 cm दूरी पर बिंदु P स्थित है। बिंदु P से दो स्पर्श रेखाऐं PQ तथा PR खींची गई तब चतुर्भुज PQOR का क्षेत्रफल ज्ञात करें?
View SolutionFrom a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral POQR is
View SolutionFrom a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Find the area of quadrilateral PQOR,
View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
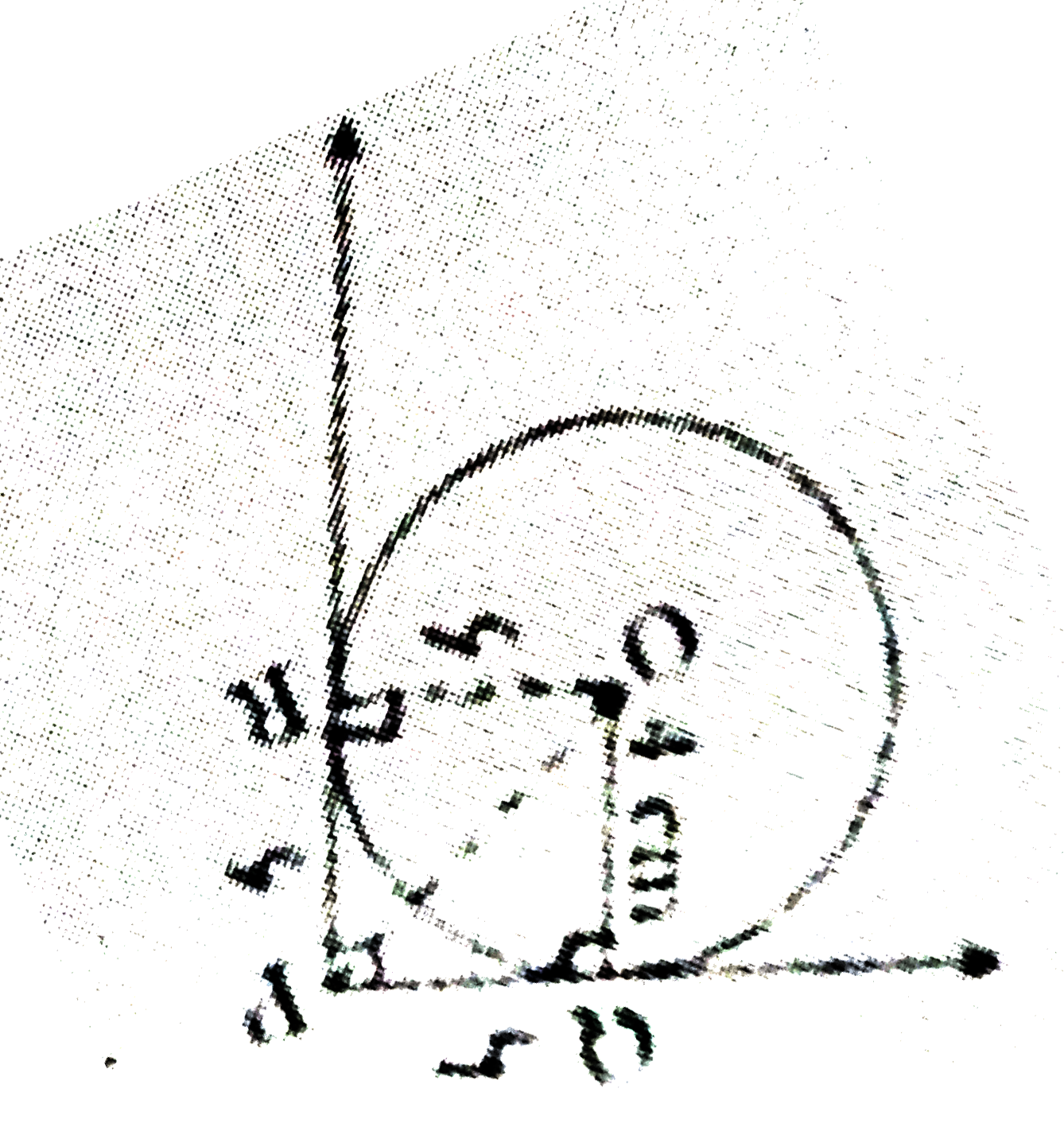
View Solutionएक बिन्दु P से जो 5 सेमी त्रिज्या के वृत्त के केन्द्र O से 13 सेमी दूर है, वृत्त की दो स्पर्श रेखायें PQ और PR खींची गई है। चतुर्भुज PQOR का क्षेत्रफल ज्ञात कीजिए।
View Solutionकिसी बिन्दु P से, जो त्रिज्या 5 सेमी वाले एक वृत्त के केन्द्र O से 13 सेमी की दुरी पर है, वृत्त पर दो स्पर्श रेखाएँ PQ और PR खींची गई है। चतुर्भुज PQOR का क्षेत्रफल है :
View SolutionO The length of the radius of the central circle is 5 cm. . 13 cm from point O. P is a point in the distance. Length of two tangents to the circle from point P PQ and PR, area of quadrilateral PQOR
View SolutionFrom a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral PQOR is
View SolutionFrom a point P, the length of the tangent to a circle is 12 cm, and the distance of P from the centre is 13 cm. The radius of the circle is
View SolutionThe radius of a circle with centre O is 5cm. P is a point at a distance 13cm from O. PQ and PR are two tangents to this circle. Find the area of the quadrilaterral PQOR.
View SolutionFrom a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is :
View Solution
