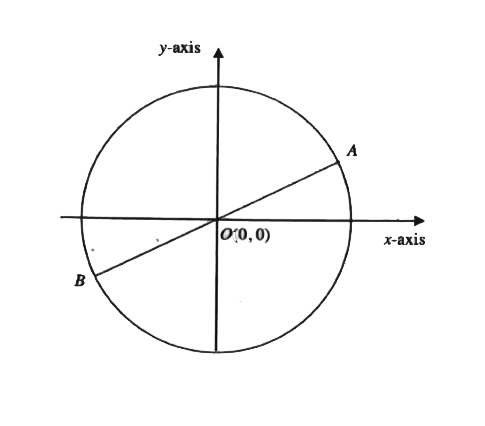
AB is a diameter of the circle with centre at O. R is any point on the circumference of the circle. If ∠ROA=120∘, then firnd the volue of ∠RBO/Solution in Bengali
60∘
Topper's Solved these Questions
Similar Questions
A hollow cylindrical pipe open at two ends is made of iron and its thickness is 2 cm. If the external diameter of the pipe be 50 cm and length be 140 cm, how many cubic centimetres of iron does it contain ?
View SolutionIn ΔPQR and ΔDEF, PQDE=QREF=RPFD. Then which one of the following is correct?
View SolutionAB, एक वृत का व्यास है, जिसका केंद्र O है। P वृत की परिधि पर एक बिन्दु है। यदि ∠POA=120∘है, तो ∠PBO का माप क्या है
View Solutionकिसी वृत्त का वायस AB है और उसका केंद्रे O है तथा उसकी परिधि पर P एक बिंदु है यदि कौन POA =120∘ हो तो कौन PBO का मान ज्ञात कीजिये ?
View SolutionAB is diametr of the circle with centre at O and P is any point on the circle. If ∠AOP=120∘ then ∠PBO=
View SolutionIn the adjoining figure, O is the centre of the circle and AB is one of its diameter . If ∠ADC=120∘ , then the value of ∠BAC is
View SolutionIn the figure shown , AB is a diameter of the circle and O is the center of the circle If A=(3,4), then what is the circumference of the circle?
View Solutionएक वृत्त का व्यास AB है तथा C उसकी परिधि पर स्थित एक बिन्दु है, तब
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle, then :
View SolutionABCD एक चतुर्भज है जिसके बिन्दु A, B, C D एक वृत्त की परिधि पर है। यदि AB वृत्त का व्यास हो तथा ∠ADC=120∘ हो, तो ∠BAC होगा
View SolutionAB is a diameter of a circle and 'C' is any point on the circumference of the circle .Then
View SolutionPQ is tangent drawn from point P to a circle with centre O and QR is a diameter of the circle, such that ∠POR=120∘. Then, ∠OPQ=……...
View SolutionAB is a diameter of a circle with centre at O. C is any point on the circle. If ∠BOC=110∘, then ∠BAC =
View SolutionAB is a diameter of a circle. C is any point on the circle, ∠ACB=
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then
View Solution
