Find the mean, median and mode of the following frequency distribution:

Text Solution
Let us draw the following table:

Let us take , A = 115 as the origin, which is the mid-value of the interval (110-120) and class length, c = 10
∴u=x−11510⇒−x=115+10−u∴−u=∑uf∑f=231300=0.77
∴−x=115+10−u=115+10×0.77=115+7.70=122.70
∴ Arithmetic mean = 122.70
To determine the median, let us draw the following table:

Here , total frequency, n=300andn2=3002=150 The number 150 lies between 50 and 150. ∴ the median lies in the interval 110-120. Here, xl=110,F=50,f0=100andc=100
∴ The mode M0=xl+f0−f−12f0−f−1−f1×c
Here, xl=110,f0=100,f−1=f1=17andc=10
∴ The mode =100+100−102×100−10−17×10=110+90×10200−27
=110+900173=19030+900173=19930173
=115.20
∴ The required mean = 122.70, median = 120 and mode = 115.20
|
Topper's Solved these Questions
Similar Questions
Find mode of the following frequency distribution.
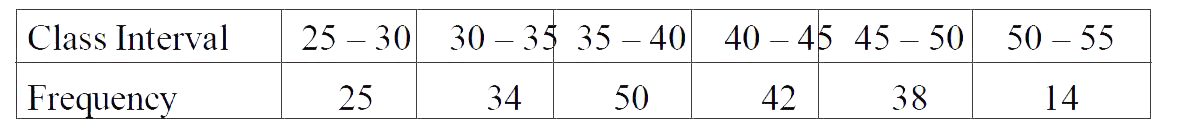
View SolutionFind the mean, median and mode of the following data

View SolutionFind the mode of the following frequency distribution:

View SolutionFind the mode of the following frequency distribution

View SolutionFind the mode of the following frequency distribution

View SolutionFind the mode of the following frequency distribution
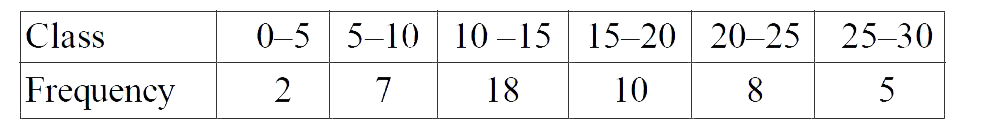
View SolutionFind the mean, median and mode of the following data.

View SolutionFind the mean, median and mode of the following data:
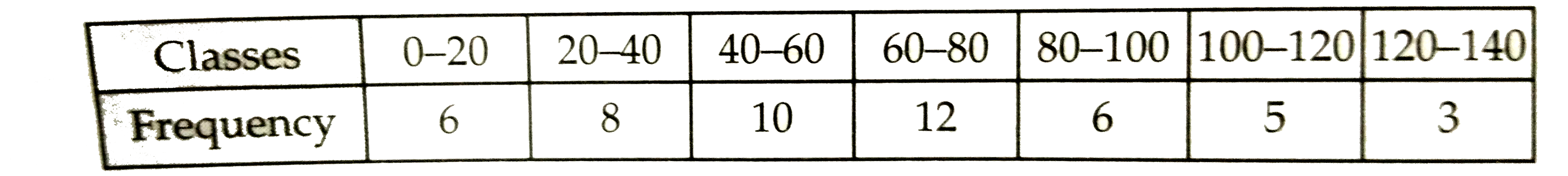
View SolutionFind the mode of the following frequency distribution.

View SolutionFind the mode of the following frequency distribution.
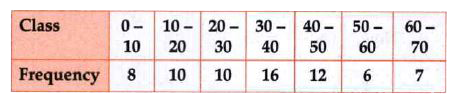
View Solution
