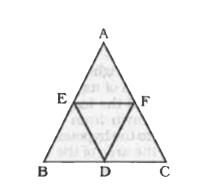
lf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
F,E is bisect ofAB&AC
=FE∣∣BC
=FE∣∣BD
BD=BF=FD
=FEDBis a ||gram
∠FED=∠DBF=60∘
similarly
FD||EC&DE||AF
∠DFE=∠ECD=60∘
&∠FDE=∠FAE60∘
∠DEFis an equilateral triangle
Similar Questions
lf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View Solution