Consider two points $P_{1} (2, 7)$ and $P_{2} (6, 15)$ . Write the equation and draw a straight line through these points.

A

$y = 2 x + 3$

B

$y = 2 x + 5$

C

$y = x + 3$

D

$2 y = 2 x + 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Step 1. Obtain the gradient or slope, which is $m$ .
Step 2. c can be found by using the $(x, y)$ values at any given point.
Step 1. Gradient $= \frac{x_{2} - y_{1}}{x_{2} - x_{1}} = \frac{15 - 7}{6 - 2} = \frac{Height}{Distance} = \frac{8}{4} = 2$
So, $y = 2 x + c$ .

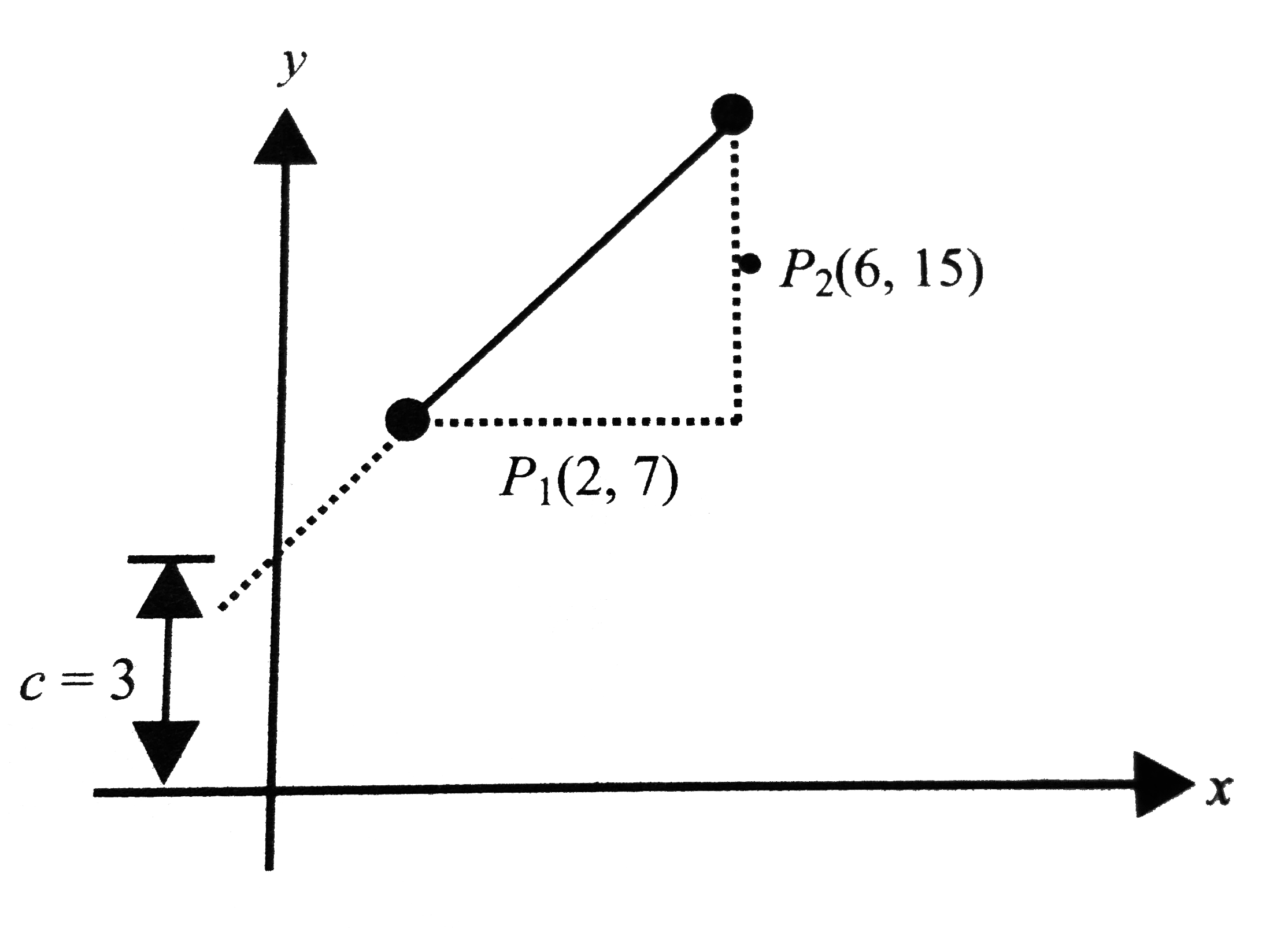
Step 2. To find $c$ , put $x = 2, y = 7$ or $x = 6, y = 15$ in Eq. (i).
$7 = 2 \times 2 + c \Rightarrow c = 3$
So, $m = 2, c = 3$ .
Hence, the equation becomes $y = 2 x + 3$ .

|

Updated on:21/07/2023

Class 11 PHYSICS BASIC MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The differential equation of all straight lines passing through the point (1,-1) is
A $y = (x + 1) \frac{d y}{d x} + 1$
B $y = (x + 1) \frac{d y}{d x} - 1$
C $y = (x - 1) \frac{d y}{d x} + 1$
D $y = (x - 1) \frac{d y}{d x} - 1$
Question 2 - Select One
The equation of a straight line passing through the points $(- 5, - 6) and (3, 10)$ is
A $x - 2 y = 4$
B $2 x - y + 4 = 0$
C $2 x + y = 4$
D $x - 2 y + 4 = 0$
Question 3 - Select One
Equation of straight line passing through the points $(2, 0) and (0, - 3)$ is
A $\frac{x}{2} - \frac{y}{3} = 1$
B $\frac{y}{3} - \frac{x}{2} = 1$
C $\frac{x}{3} - \frac{y}{2} = 1$
D $\frac{y}{2} - \frac{x}{3} = 1$

CENGAGE PHYSICS-BASIC MATHEMATICS-Exercise 2.6

Home
Ask Doubt
Profile