ˆi and ˆj are unit vectors along x-and y-axes respectively. What is the magnitude and the direction of the vectors ˆi+ˆj and ˆi−ˆj? What are the components of a vector →A=2ˆi+3ˆj along the direction ˆi+ˆjand ˆi−ˆj?
Video Solution
Text Solution
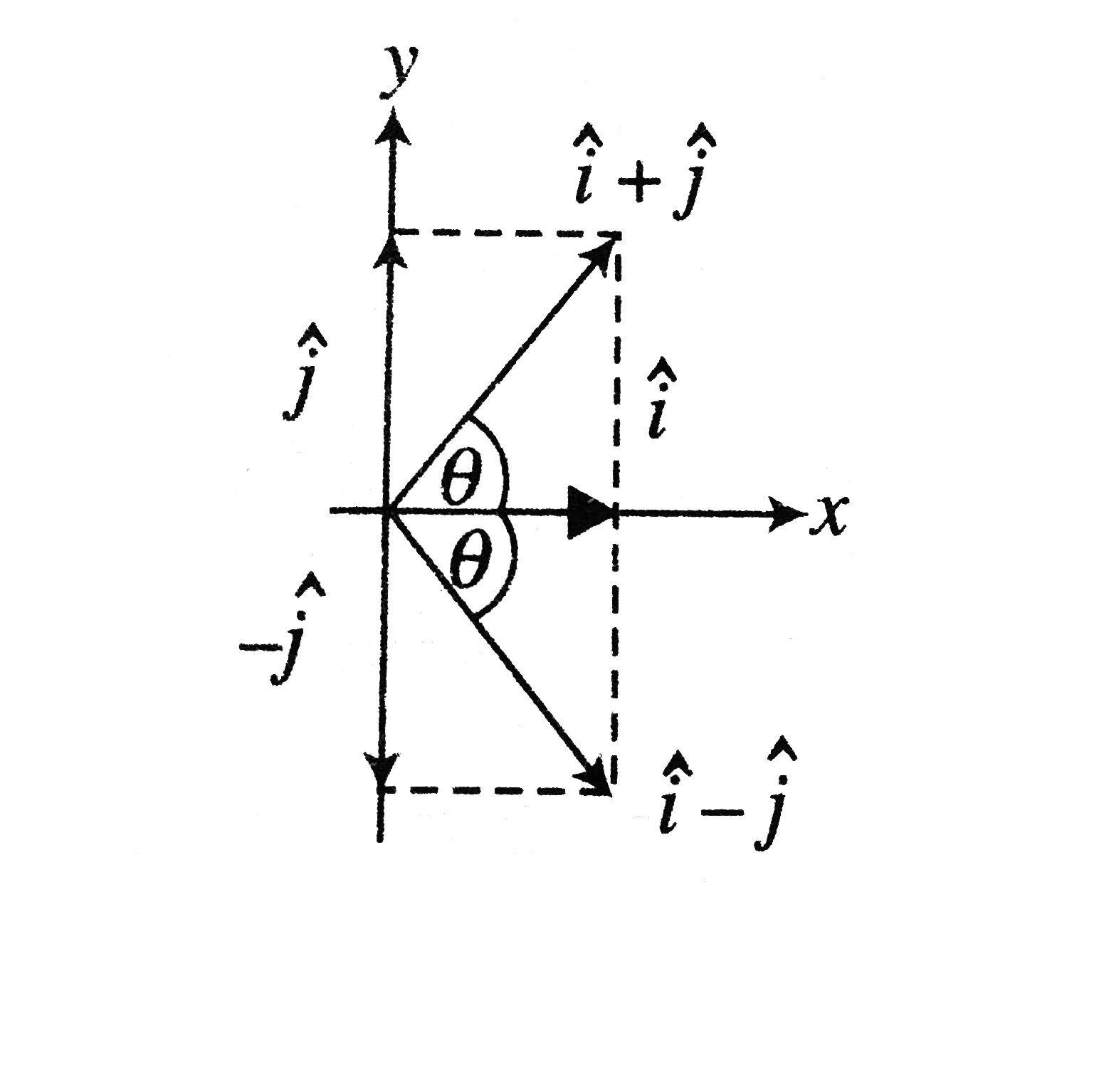
a.∣∣ˆi+ˆj∣∣=√12+12+2×1×1×cos90∘
=√2=1.414 units
tanθ=11=1
∴θ=45∘
So, the vector ˆi+ˆj makes an angle of 45∘ with x-axis.
b. ∣∣ˆi−ˆj∣∣=∣∣ˆi+(−ˆj)∣∣
=√12+(−1)2+2(1)(−1)cos90∘=√2
tanθ=1−1=−1∴θ=−45∘
The vector →A=2ˆi+3ˆj makes an angle of −45∘ with x=axis.
Let us know determine the component of →A=2ˆi+3ˆj in the direction of ˆi+ˆj.
Then, →B=ˆi+ˆj
→A.→B=ABcosθ=(Acosθ)B
So component of →A in the direction of →B
=→A⋅→BB=(2ˆi+3ˆj).(ˆi+ˆj)√12+12=2.1+3.1√2=5√2 units
Component of →A in the direction of ˆi−ˆj
(2ˆi+3ˆj).(ˆi−ˆj)√2=−1√2 units.
Here,PM is the component of →A in the direction of →B. So, dot product of two vectors →A and →B may be defined as the product of the magnitude of →B and the component of →Ain the direction →B.
|
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.1
19 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
Knowledge Check
The component of vector A=2ˆi+3ˆj along the vector ˆi+ˆj is
A5√2B10√2C5√2D5What is the vector equally inclined to the vectors ˆi+3ˆjand3ˆi+ˆj ?
Aa) hat(i) + hat(j)Bb) 2 hat(i)- hat(j)Cc) 2 hat(i) + hat(j)Dd) none of theseWhat is the vector equally inclined to the vectors ˆi+3ˆjand3ˆi+ˆj?
Aˆi+ˆjB2ˆi−ˆjC2ˆi+ˆjDNone of these
Find the component of a vector →A=3ˆI+4ˆj along the direction of 2ˆI−3ˆj.
View SolutionFind the component of a vectro →A=3ˆI+2ˆj along the direction of (ˆI+ˆj)
View SolutionFind the projection of the vector ˆi−ˆjon the vector ˆi+ˆj
View SolutionIf ˆi,ˆjandˆk are unit vectors along x,y and z-axis respectively, the angle θ between the vector ˆi+ˆj+ˆk and vectorˆj is given by
View SolutionWhat is the projection of the vector ˆi−2ˆj−ˆk on the vector 4ˆi−4ˆj+7ˆk?
View Solution
