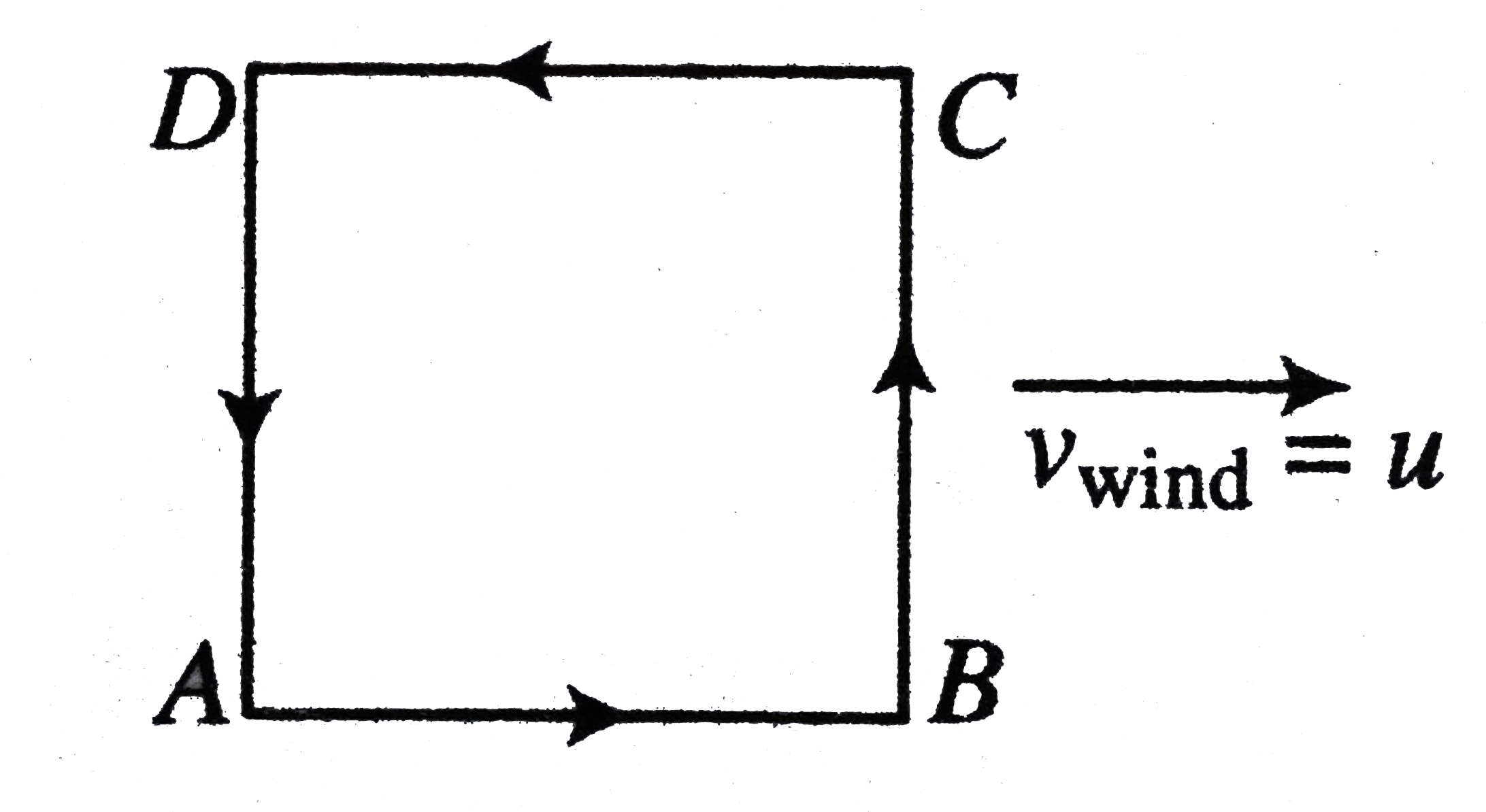
Find the time an aeroplane having velocity v takes to fly around a square with side a if the wind is blowing at a velocity u along one side of the square.\
Velocity of aeroplane while flying through AB,
vA=v+u
tAB=av+u
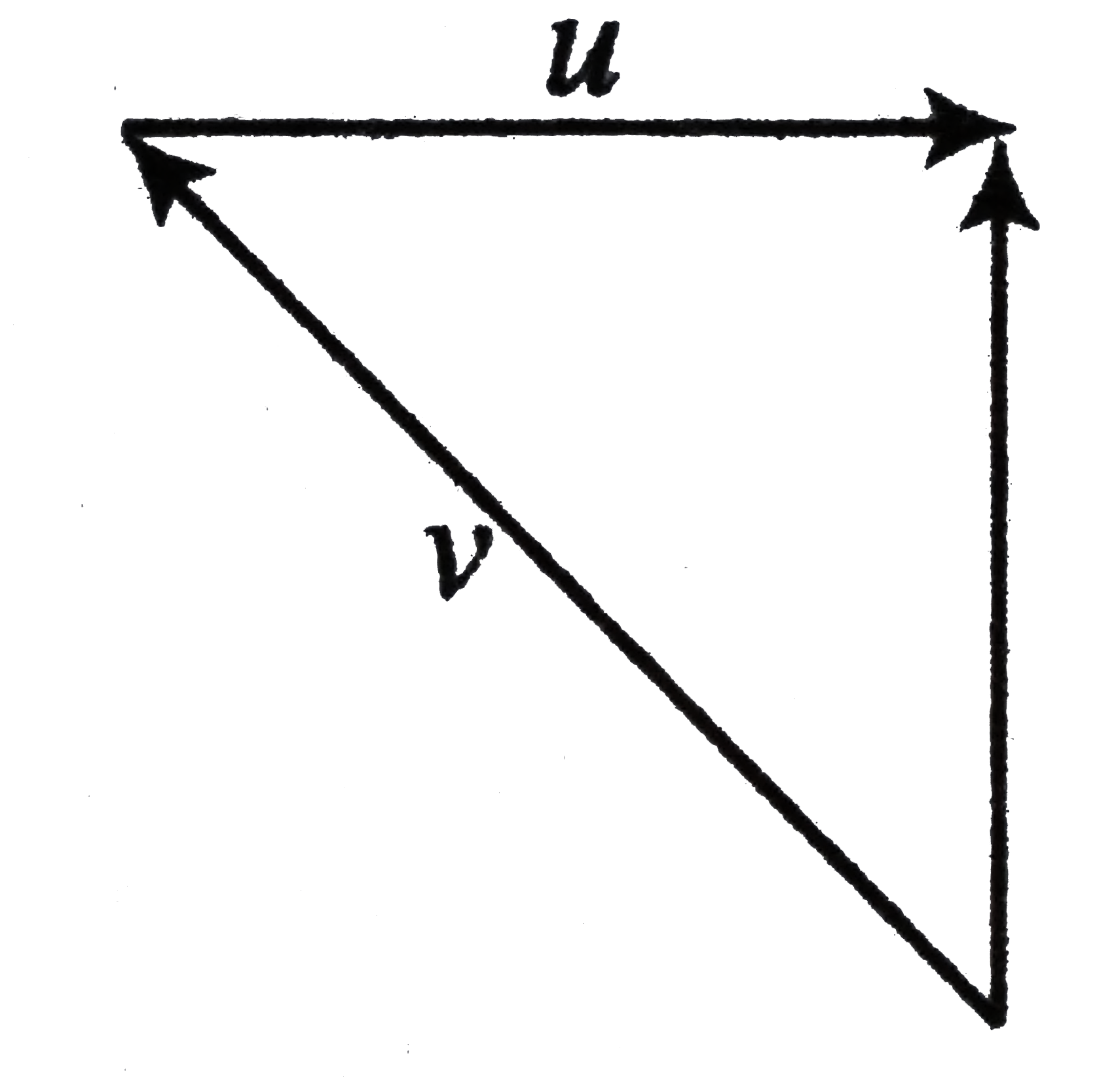
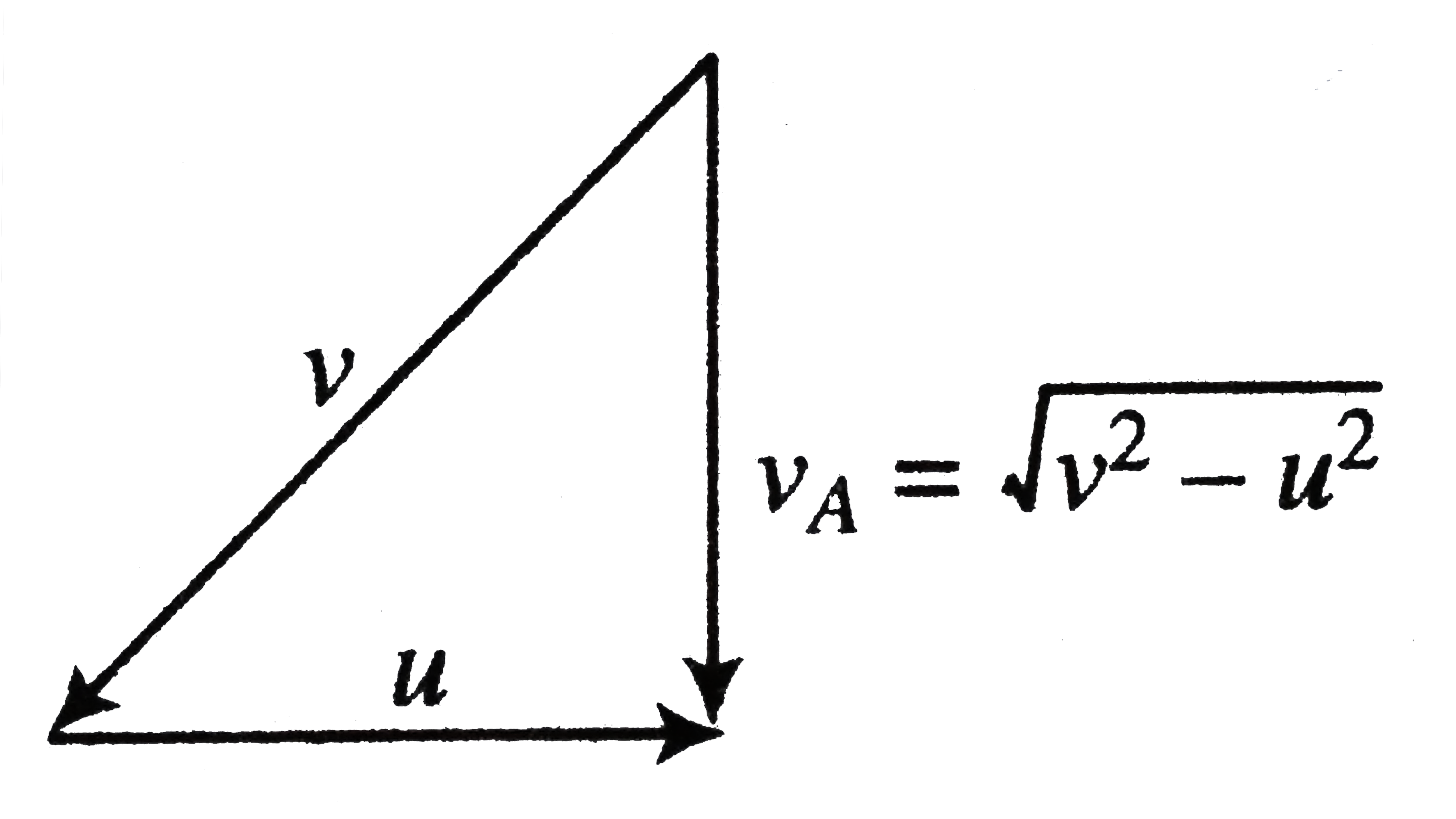
Velocity of aeroplane while flying through BC,
vA=√v2−u2
tBC=a√v2−u2
Velocity of aeroplane while flying through CD
vA=v−u
tCD=av−u
Velocity of aeroplane while flying through DA,
vA=√v2−u2
tDA=a√v2−u2
Total time =tAB+tBC+tCD+tDA
=av+u+a√v2−u2+av−u+a√v2−u2
=2av2−u2(v+√v2−u2).
 ,
,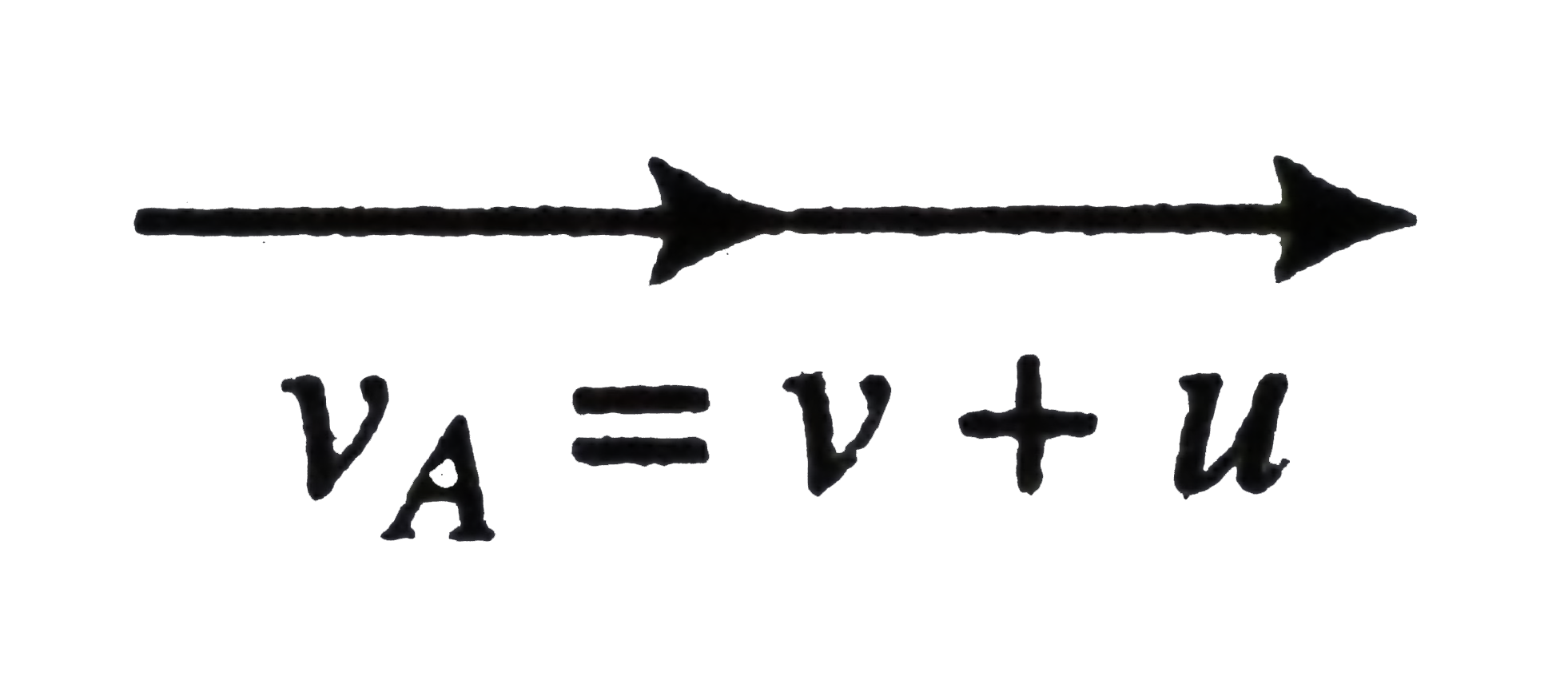 ,
, ,
,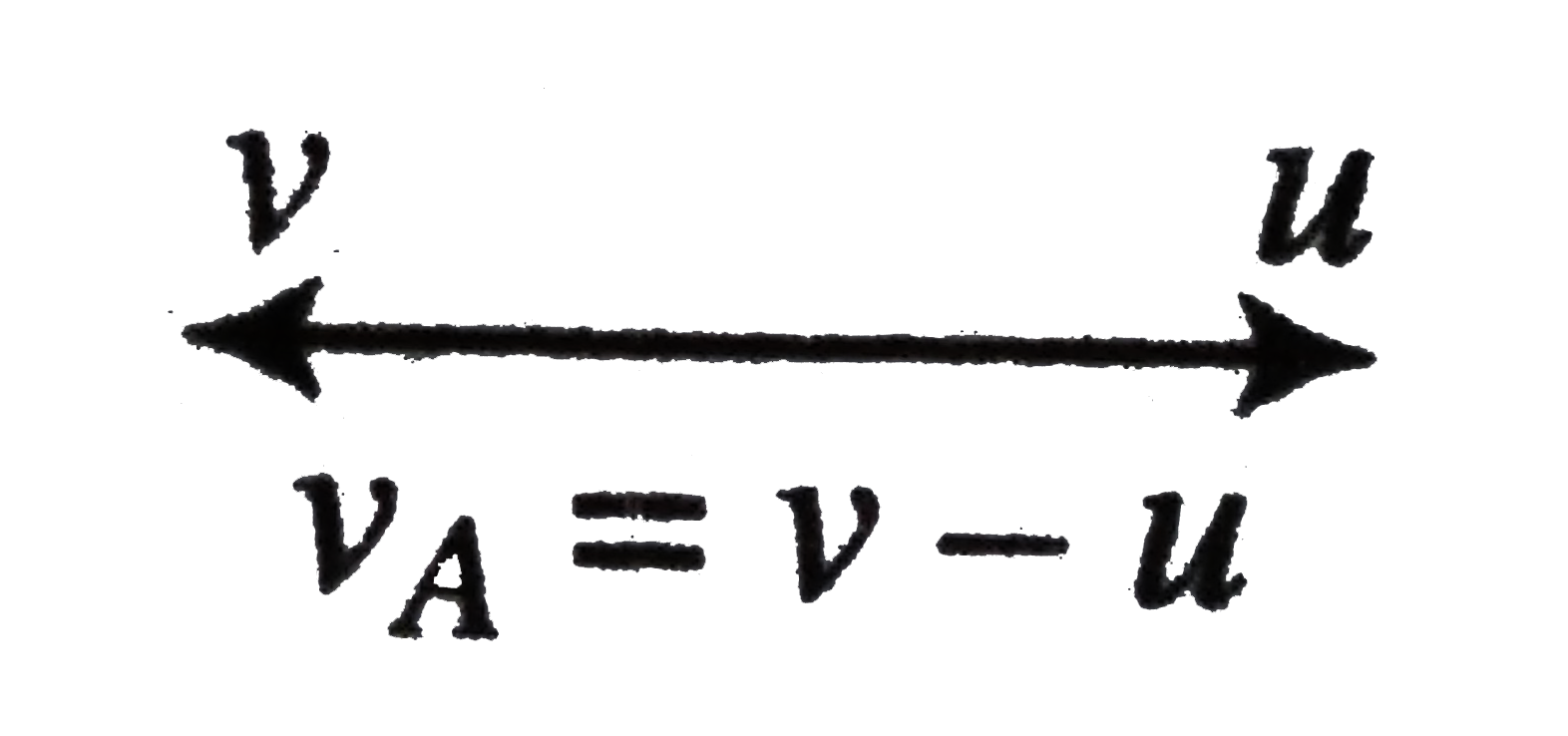 ,
,
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
How long will a plane take to fly around a square with side a with the wind blowing at a velocity u, in the two cases (a) the direction of the wind coincides with one of the sides (b) the direction of the wind coincides with one diagonal of the square. The velocity of the plane in still air is v>u..
View SolutionA plane takes t×102 seconds to fly around a square with side 3.5km when the wind is blowing steady at a speed 30√2ms parallel to one of the diagonals of square.The velocity of plane in still air is 50m/s .Find t.
View Solution
Knowledge Check
If the side of an square is a, then find the side of the regular octagon that can be inscribed in this square.
AA)a1+√2√2BB)a3CC)a2+√2DD)none of theseThe midpoints of alternating sides of a regular octagon are joined to form a square. If each side of the octagon is a, find each side of the square.
A(2+√2)a2B(4+√2)a2C2(1+√2)a√2D(2+√2)a
Ina square one diagonal is 16cm .Find the side of the square
View SolutionA vertex of a square is at the origin and its one side lies along the line 3x-4y-10=0. Find the area of the square.
View SolutionLength of the diagonal of a square is 12 cm. Find the length of each side of the square.
View SolutionIf one side of the square is 2x−y+6=0, then one of the vertices is (2,1) . Find the other sides of the square.
View SolutionIf the length of a diagonal of square is 6cm. Find the length of the side of the square.
View SolutionTwo squares have sides xcm and (x+4) . The sum of their areas is 656cm2 . Find the sides of the squares.
View Solution
