Question

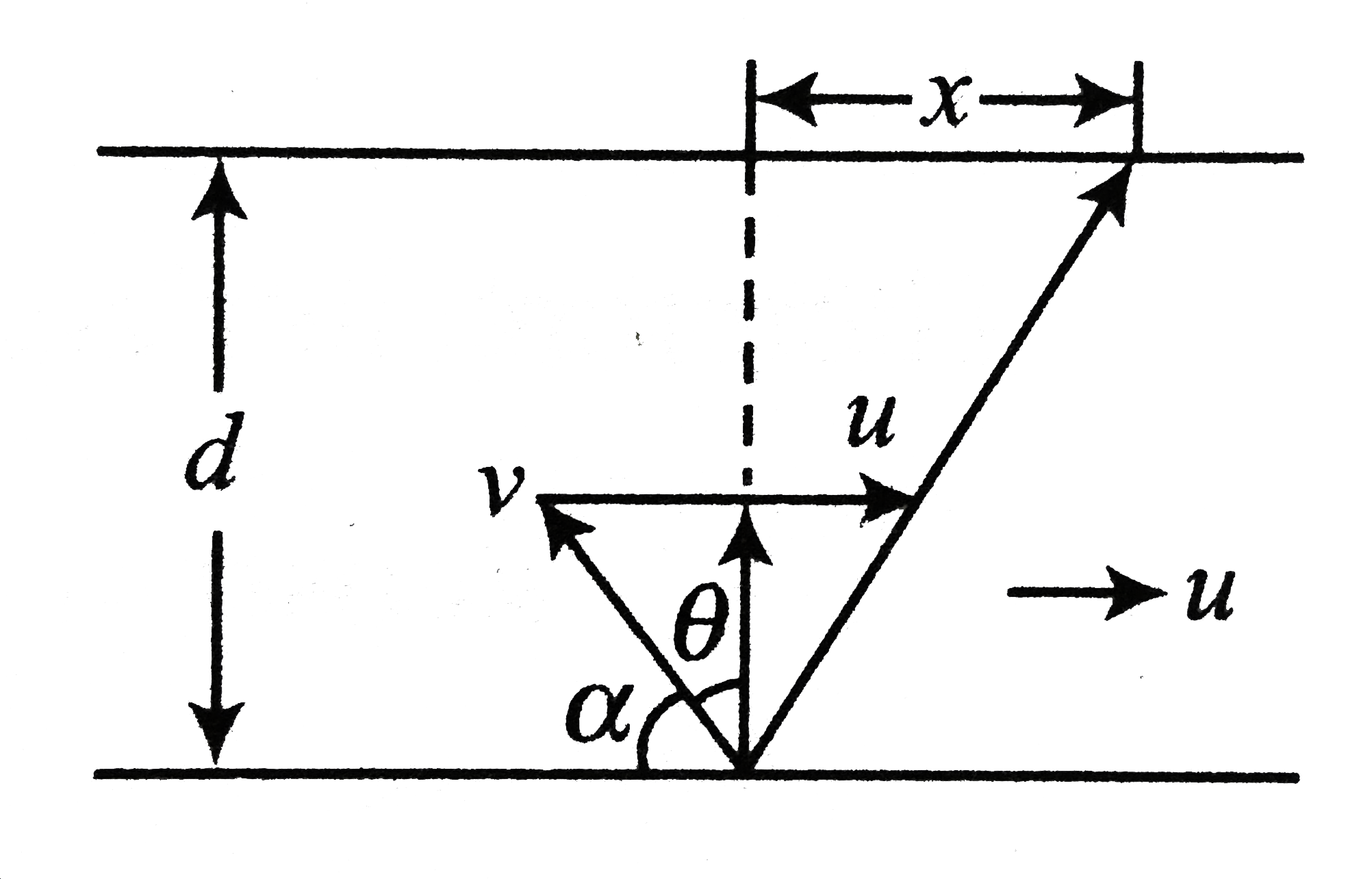
The velocity if a swimmer $\left(v\right)$ in stil water is less than the velocity of water $\left(u\right)$ in a river. Show that the swimmer must aim himself at an angles ${\cos }^{-1}$ $(v/u)$ with upstream in order to cross the river along the shortest possible path. Find thr drifting (distance moved along the direction of stream in crossing the river) of the swimmer along this shortest possible path.

Answer

`((sqrt(u^2 - v^2)) d)/(v)`.

Explanation

`x = ((u - v sin theta)/(cos theta)) (d)/(v) rArr (d x)/(d theta) = 0 rArr theta = (v)/(u)`
`cos prop = (v)/(u) rArr prop = cos^-1 ((v)/(u))`
We can get
`x = ((u - (v^2)/(u))(d)/(v))/(sqrt(1 - (v^2)/(u^2))) = ((sqrt(u^2 - v^2))d)/(v)`.
.