A small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width $x (x < < 2 R)$ . (All the surfaces are frictionless).

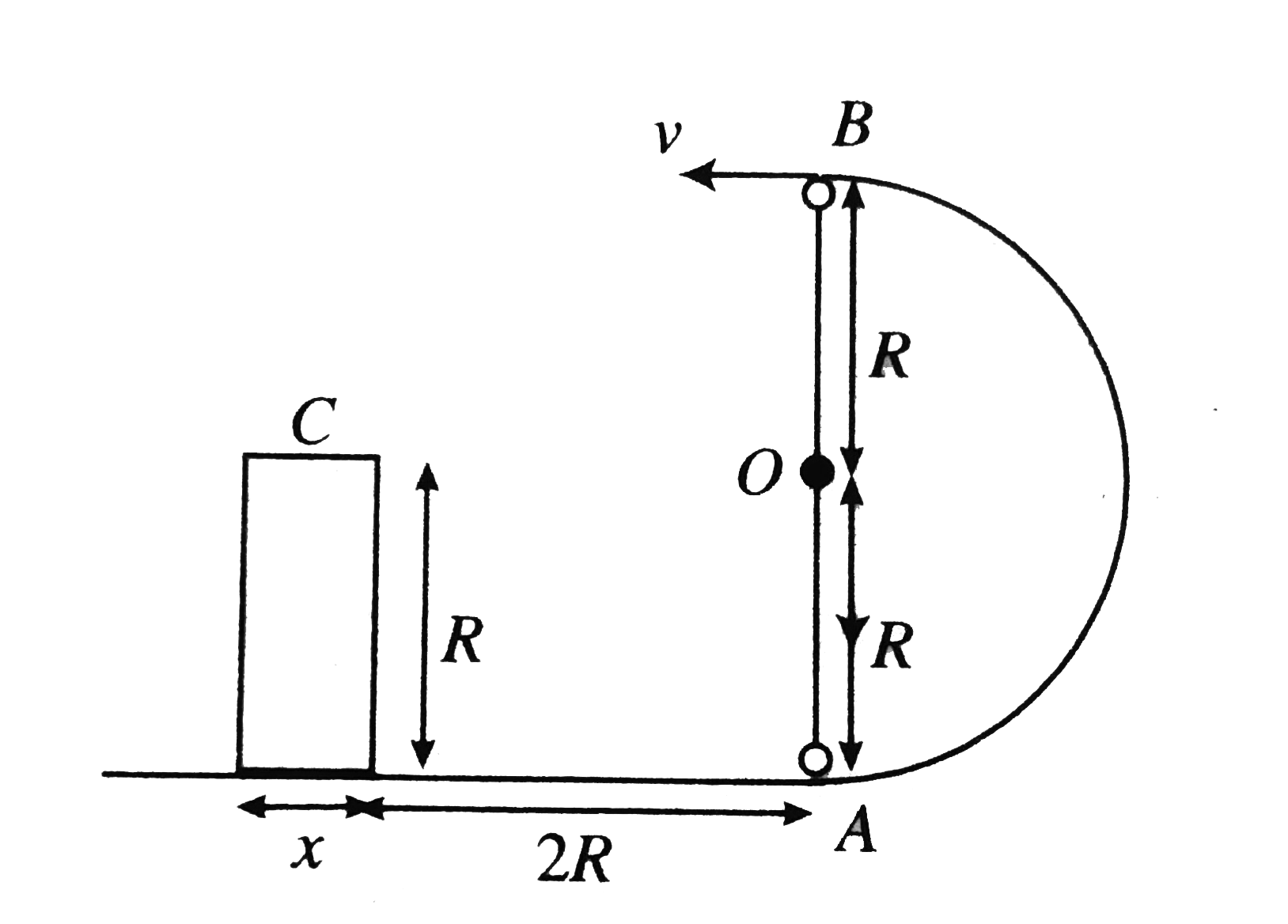
If the collision of ball with the building is elastic, then the angle with the horizontal at which the ball will rebound from the top of the building is

A

(a) $60^{\circ}$

B

(b) $45^{\circ}$

C

(c) $30^{\circ}$

D

(d) None

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$v_{y} = g t$
$v_{y} = g \sqrt{\frac{2 R}{g}} = \sqrt{2 g R}$ , $v_{x} = \sqrt{2 g R}$
$tan θ = \frac{v_{y}}{v_{x}} = 1$
$θ = 45^{\circ}$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width $x (x < < 2 R)$ . (All the surfaces are frictionless).

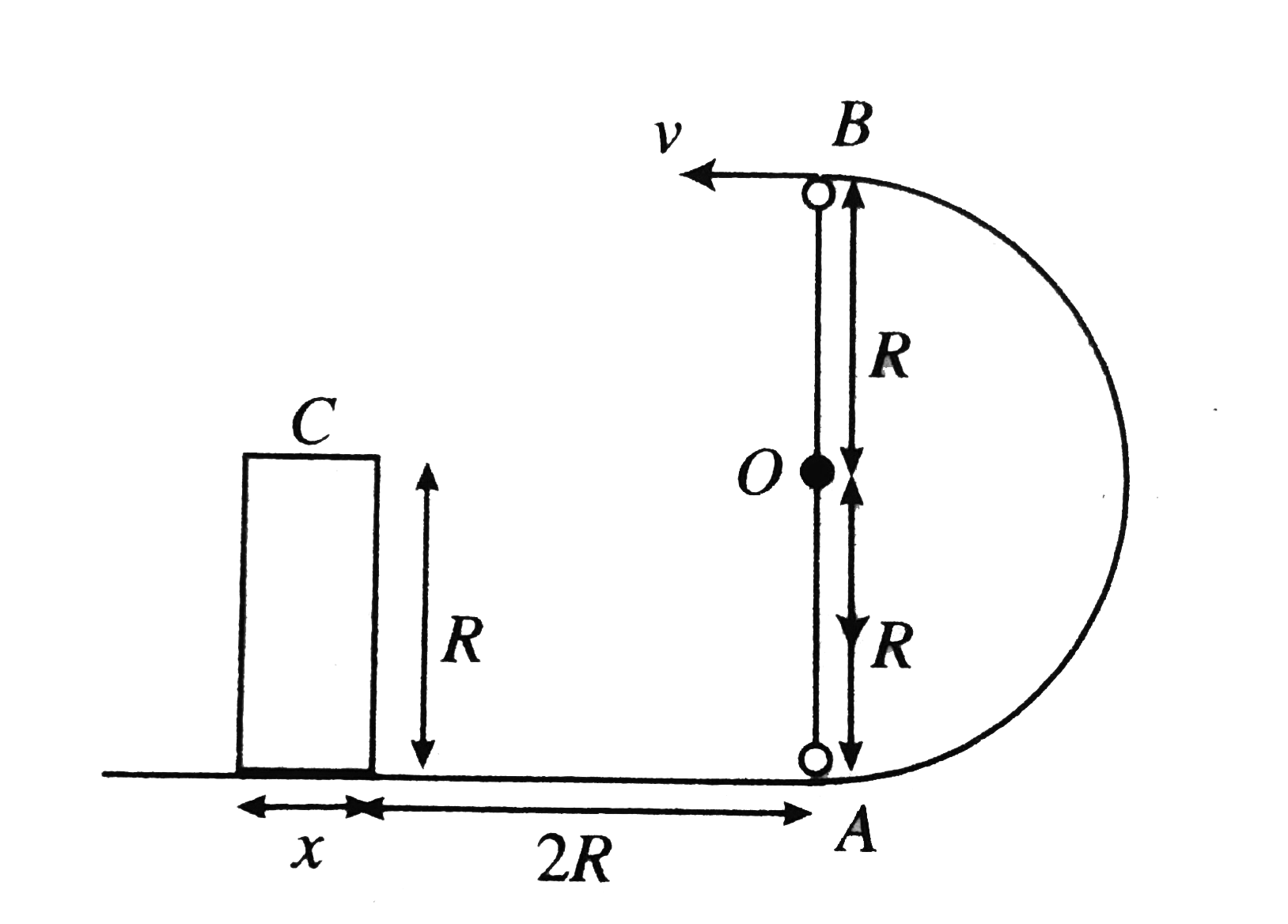
The horizontal distance of the ball from the foot of the builing where the ball strikes the horizontal ground will
A(a) $\sqrt{2} R$
B(b) $(1 + \sqrt{2}) R$
C(c) $2 (1 + \sqrt{2}) R$
D(d) $12 R$
Question 2 - Select One
A small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width $x (x < < 2 R)$ . (All the surfaces are frictionless).

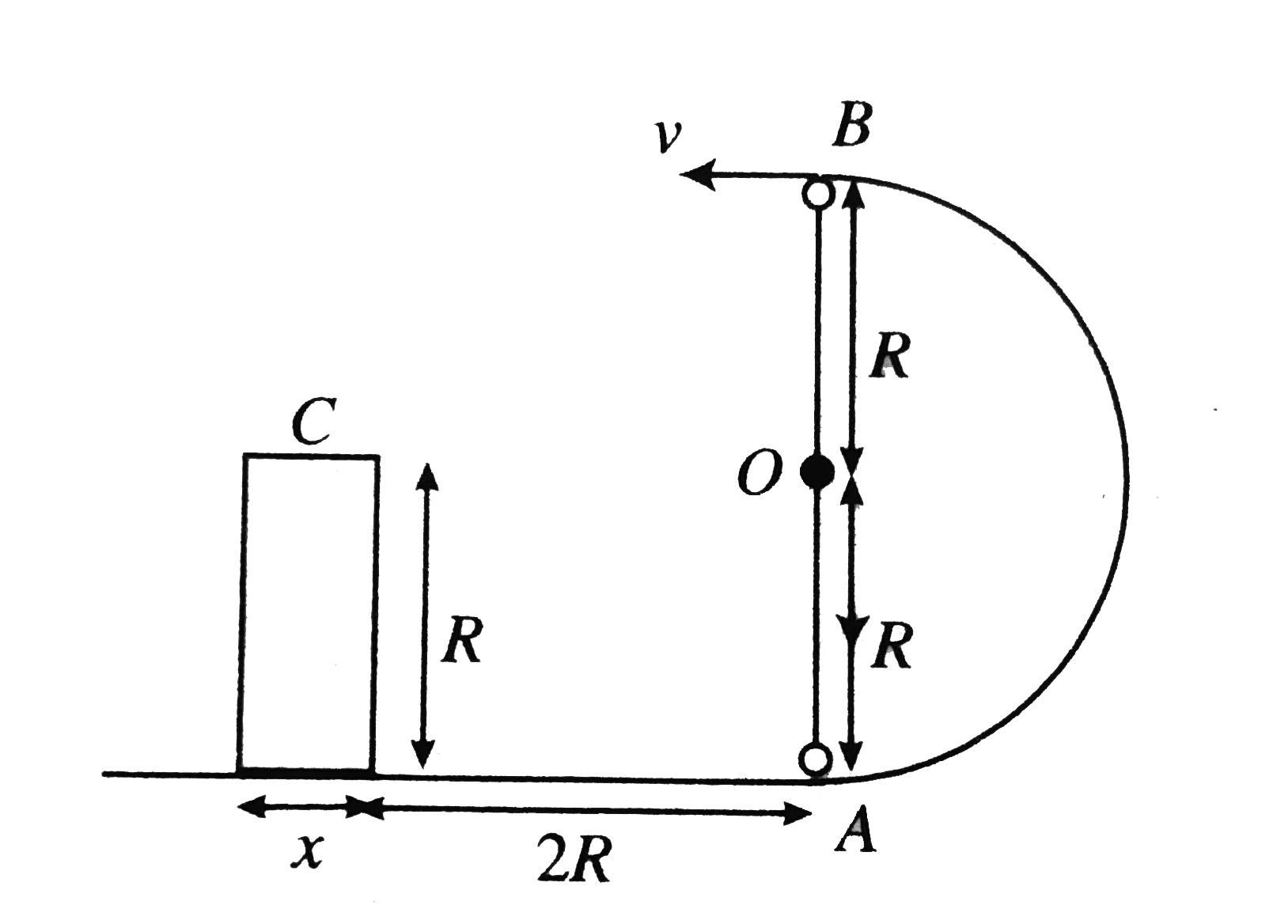
The velocity given to the ball at point A so that it may hit the top of the building is
A(a) $\sqrt{4 g R}$
B(b) $\sqrt{2 g R}$
C(c) $\sqrt{g R}$
D(d) $\sqrt{6 g R}$
Question 3 - Select One
If a ball is thrown up with a velocity v from the top of a building the ball reaches the ground with a velocity 3u. Find the height of the building.
A $9 u^{2} / g$
B $6 u^{2} / g$
C $4 u^{2} / g$
D $3 u^{2} / g$

CENGAGE PHYSICS-WORK, POWER & ENERGY-Linked Comprehension

Home
Ask Doubt
Profile