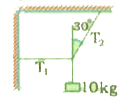
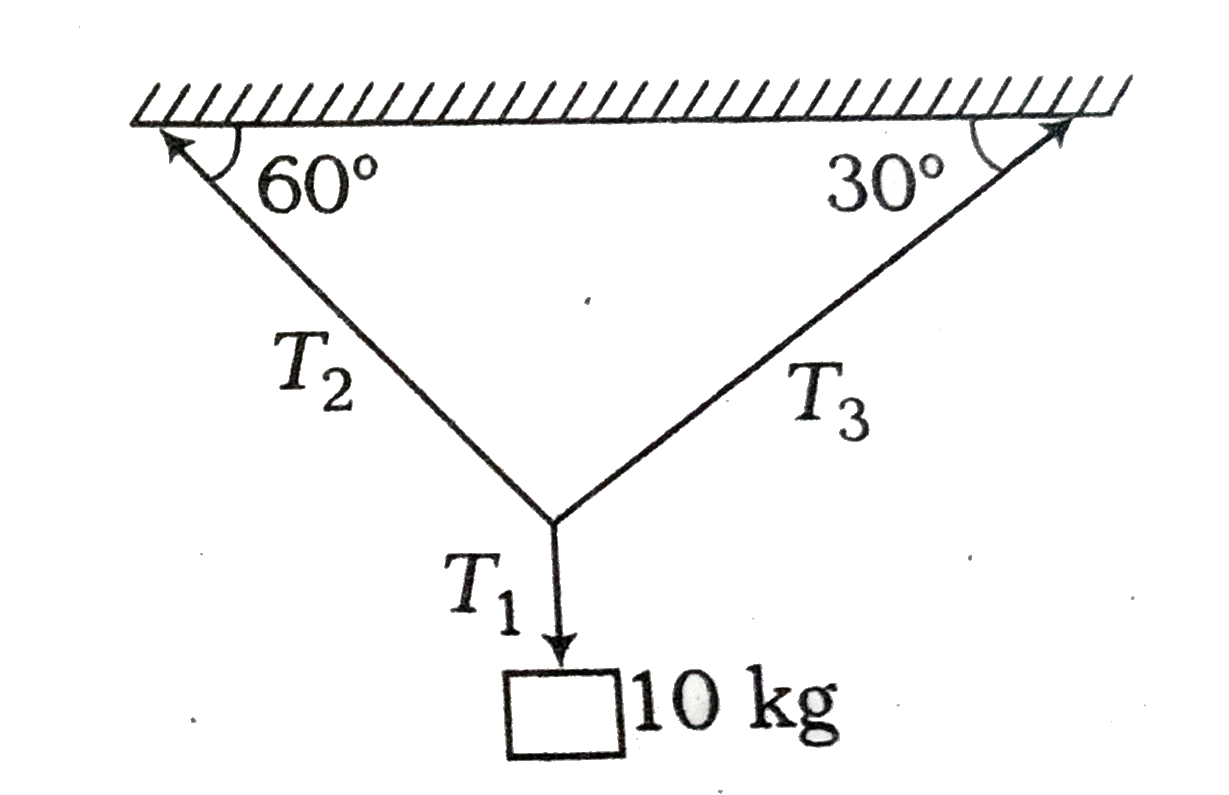
A block of mass 10 kg is suspended by three strings as shown in the figure. The tension $T_{2}$ is

$100 N$

$\frac{100}{\sqrt{3}} N$

$\sqrt{3} \times 100 N$

$50 \sqrt{3} N$

Text Solution

Verified by Experts

The correct Answer is:D

$T_{3} {sin 60}^{\circ} = T_{2} {sin 30}^{\circ}$
$∴ T_{3} = \frac{T_{2}}{\sqrt{3}}$

Now, $T_{2} {cos 30}^{\circ} + T_{3} {cos 60}^{\circ} = T_{1} = 100$
or $\frac{\sqrt{3} T_{2}}{2} + \frac{T_{2}}{\sqrt{3}} \times \frac{1}{2} = 100$ or $\frac{8 T_{2}}{4 \sqrt{3}} = 100$
$T_{2} = 50 \sqrt{3} N$

Updated on:21/07/2023

Class 12 PHYSICS FORCE

Topper's Solved these Questions

BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)
19videos
FORCE
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)
19videos
FORCE
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29videos
ELECTROSTATICS
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)
24videos
FRICTION IN SOLID AND LIQUIDS

Knowledge Check

Question 1 - Select One
A block of mass 10 kg is suspended by three strings as shown in figure . Tension $T_{2}$ is

A100N
B $\frac{100}{\sqrt{3}} N$
C $\sqrt{3} \times 100 N$
D $50 \sqrt{3} N$

A block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

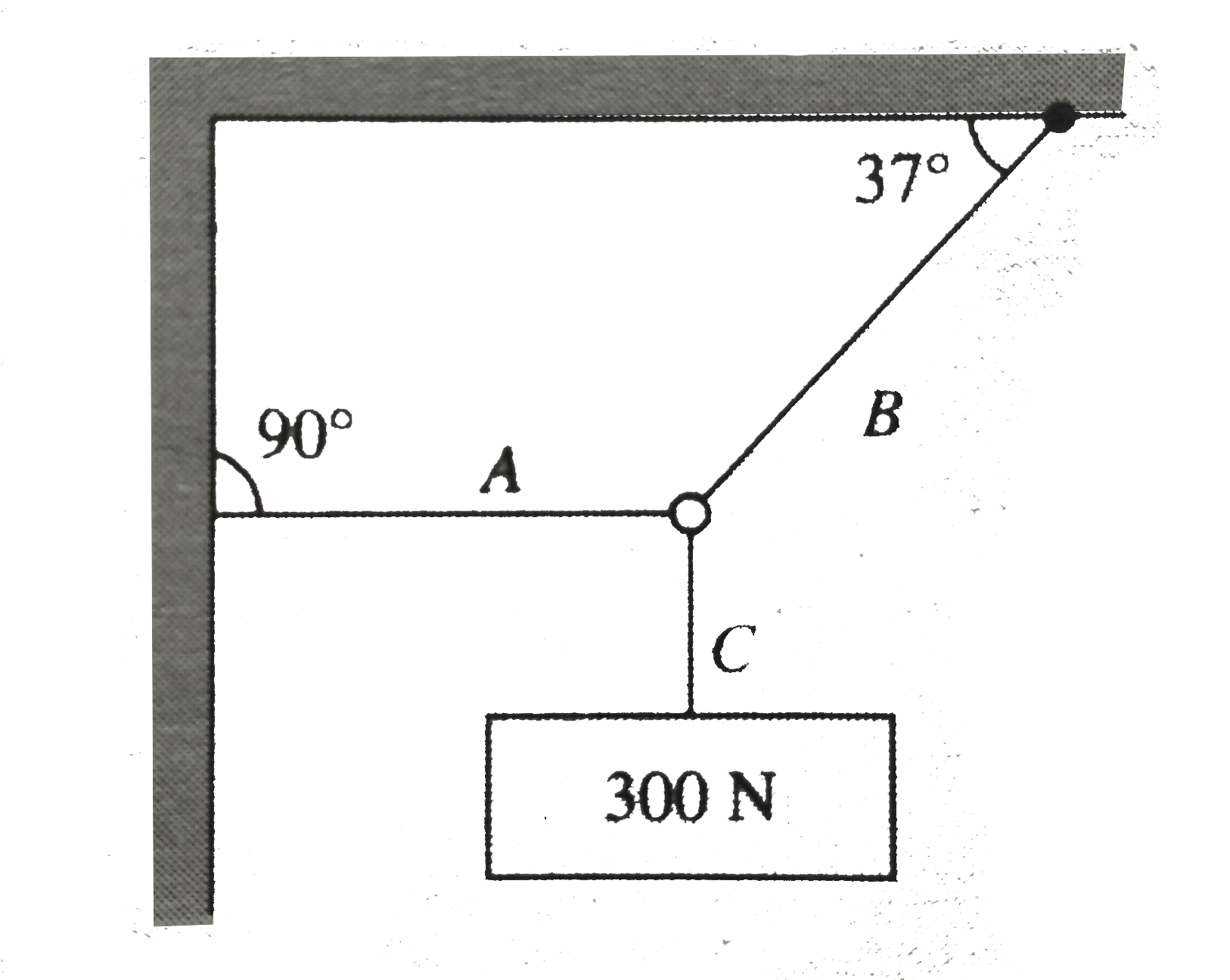
View Solution
A block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View Solution
A 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. $(g = 10 m / s^{2})$

View Solution
A block of mass 20kg is balanced by three strings A, B & C as shown in figure. Ratio of tensions in strings AC and $B C (T_{A} / T_{B})$ is

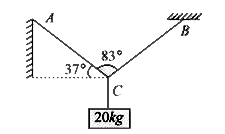
View Solution
A block of mass 20kg is balanced by three strings A, B & C as shown in figure. Ratio of tensions in strings AC and $B C (T_{A} / T_{B})$ is

View Solution
A block of mass 20kg is balanced by three strings A, B & C as shown in figure. Ratio of tensions in strings AC and $B C (T_{A} / T_{B})$ is

View Solution
A block of mass 10 kg is suspended throug two light spring balances as shown in figure

View Solution

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-FORCE-Exercise 1

Three blocks are placed at rest on a smooth inclined plane with force ...
Text Solution
In the arrangement shown, the mass m will ascend with an acceleration ...
Text Solution
A block of mass 10 kg is suspended by three strings as shown in the fi...
Text Solution
If impulse I varies time t as I(kg ms^(-1))=20t^(2)-40t. The change ...
01:51
An initially stationary device lying on a frictionless floor explodes ...
Text Solution
A bullet of mass 10 g is fired from a gun of mass 1 kg with recoil vel...
04:00
A bullet of mass 0.1 kg is fired with a speed of 100 ms^(-1). The mass...
03:33
A gradener pushes a lawn roller through a distance 20 m. If he applies...
02:38
How much work must work be done by a force on 50 kg body in order to a...
01:23
A force (3 hat(i)+4 hat(j)) acts on a body and displaces it by (3 hat(...
01:29
Force acting on a particale is (2hat(i)+3hat(j))N. Work done by this f...
03:07
A force F = Ay^(2)+By+C acts on a body at rest in the Y-direction. The...
04:31
The force F acting on a particle is moving in a straight line as shown...
Text Solution
If the force acting on a body is inversely proportional to its speed, ...
04:51
The kinetic energy acquired by a body of mass m in travelling a certai...
02:29
Under the action of a force, a 2 kg body moves such that its position ...
01:54
An object of mass 5 kg is acted upon by a force that varies with posit...
Text Solution
A block of mass 20 kg is moving in x-direction with a constant speed o...
04:07
In an elastic collison
01:29
If a body of mass m collides head on, elastically with velocity u with...
02:45

Home
Ask Doubt
Profile

A block of mass 10 kg is suspended by three strings as shown in the figure. The tension T2 is

The correct Answer is:D

T3sin60∘=T2sin30∘ ∴T3=T2√3 Now, T2cos30∘+T3cos60∘=T1=100 or √3T22+T2√3×12=100 or 8T24√3=100 T2=50√3N

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-FORCE-Exercise 1

A block of mass 10 kg is suspended by three strings as shown in the figure. The tension $T_{2}$ is

$T_{3} {sin 60}^{\circ} = T_{2} {sin 30}^{\circ}$
$∴ T_{3} = \frac{T_{2}}{\sqrt{3}}$

Now, $T_{2} {cos 30}^{\circ} + T_{3} {cos 60}^{\circ} = T_{1} = 100$
or $\frac{\sqrt{3} T_{2}}{2} + \frac{T_{2}}{\sqrt{3}} \times \frac{1}{2} = 100$ or $\frac{8 T_{2}}{4 \sqrt{3}} = 100$
$T_{2} = 50 \sqrt{3} N$

A block of mass 10 kg is suspended by three strings as shown in figure . Tension $T_{2}$ is