Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
GmR
√2√2GMR
√GMR(2√2+1)
√GMR2√2+14
The correct Answer is:D
To find the speed of each particle moving in a circle of radius R under the action of their mutual gravitational attraction, we can follow these steps:
Step 1: Understand the System
We have four particles, each of mass M, moving in a circle of radius R. The gravitational attraction between these particles provides the necessary centripetal force for circular motion.
Step 2: Calculate the Gravitational Force
The gravitational force F between two particles is given by Newton's law of gravitation:
F=GM2d2
where G is the gravitational constant and d is the distance between the two particles.
Step 3: Determine the Distances
In a square configuration (since there are four particles), the distance between any two adjacent particles is R, and the distance between diagonally opposite particles is √2R.
Step 4: Calculate the Net Gravitational Force on One Particle
For one particle, the net gravitational force will be the vector sum of the forces exerted by the other three particles.
1. The force from each adjacent particle (2 particles) at distance R:
Fadjacent=GM2R2
There are two such forces.
2. The force from the diagonally opposite particle (1 particle) at distance √2R:
Fdiagonal=GM2(√2R)2=GM22R2
Step 5: Calculate the Total Force
The total gravitational force acting on one particle can be expressed as:
Fnet=2Fadjacent+Fdiagonal=2(GM2R2)+GM22R2
Combining these:
Fnet=2GM2R2+GM22R2=4GM22R2+GM22R2=5GM22R2
Step 6: Relate the Net Force to Centripetal Force
For circular motion, the net gravitational force provides the centripetal force required to keep the particle moving in a circle:
Fnet=Mv2R
Setting the two expressions for force equal gives:
5GM22R2=Mv2R
Step 7: Solve for Velocity v
Rearranging the equation to solve for v2:
v2=5GM2R
Taking the square root gives:
v=√5GM2R
Final Answer
The speed of each particle is:
v=√5GM2R
We have four particles, each of mass M, moving in a circle of radius R. The gravitational attraction between these particles provides the necessary centripetal force for circular motion.
The gravitational force F between two particles is given by Newton's law of gravitation:
F=GM2d2
where G is the gravitational constant and d is the distance between the two particles.
In a square configuration (since there are four particles), the distance between any two adjacent particles is R, and the distance between diagonally opposite particles is √2R.
For one particle, the net gravitational force will be the vector sum of the forces exerted by the other three particles.
Fadjacent=GM2R2
There are two such forces.
Fdiagonal=GM2(√2R)2=GM22R2
The total gravitational force acting on one particle can be expressed as:
Fnet=2Fadjacent+Fdiagonal=2(GM2R2)+GM22R2
Combining these:
Fnet=2GM2R2+GM22R2=4GM22R2+GM22R2=5GM22R2
For circular motion, the net gravitational force provides the centripetal force required to keep the particle moving in a circle:
Fnet=Mv2R
Setting the two expressions for force equal gives:
5GM22R2=Mv2R
Rearranging the equation to solve for v2:
v2=5GM2R
Taking the square root gives:
v=√5GM2R
The speed of each particle is:
v=√5GM2R
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - MHT CET Corner20videos
GRAVITATION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - Exercise 169videos
GRAVITATION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)24videos
FRICTION IN SOLID AND LIQUIDS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner24videos
INTERFERENCE AND DIFFRACTION OF LIGHT
Similar Questions
For particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
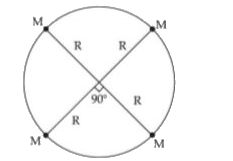 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2) - Question 2 - Select One
Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmR - Question 3 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2R
Two particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.
 View Solution
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View Solution

