A rope 1 cm in diameter breaks, if the tension in it exceeds 500 N. The maximum tension that may be given to similar rope of diameter 3 cm is
500 N
3000 N
4500 N
2000 N
The correct Answer is:c
To solve the problem, we need to determine the maximum tension that a rope with a diameter of 3 cm can withstand, given that a rope with a diameter of 1 cm breaks at a tension of 500 N.
1. Understand the relationship between tension and area:
The breaking stress (σ) of a material is defined as the force (tension, T) applied per unit area (A). It can be expressed as:
σ=TA
2. Calculate the area of the first rope:
The diameter of the first rope (D1) is 1 cm, so the radius (R1) is:
R1=D12=1cm2=0.5cm=0.005m
The cross-sectional area (A1) of the first rope is given by:
A1=πR12=π(0.005)2=π×0.000025=7.85×10−5m2
3. Calculate the breaking stress of the first rope:
Given that the maximum tension (T1) the first rope can withstand is 500 N, we can calculate the breaking stress (σ) as:
σ=T1A1=500N7.85×10−5m2≈6.37×106N/m2
4. Calculate the area of the second rope:
The diameter of the second rope (D2) is 3 cm, so the radius (R2) is:
R2=D22=3cm2=1.5cm=0.015m
The cross-sectional area (A2) of the second rope is given by:
A2=πR22=π(0.015)2=π×0.000225=7.07×10−4m2
5. Determine the maximum tension for the second rope:
Since the breaking stress remains the same for both ropes (as they are made of the same material), we can set up the equation:
σ=T2A2
Rearranging gives us:
T2=σ×A2
Substituting the values we found:
T2=(6.37×106N/m2)×(7.07×10−4m2)≈4500N
Final Answer:
The maximum tension that may be given to the similar rope of diameter 3 cm is approximately 4500 N.
The breaking stress (σ) of a material is defined as the force (tension, T) applied per unit area (A). It can be expressed as:
σ=TA
The diameter of the first rope (D1) is 1 cm, so the radius (R1) is:
R1=D12=1cm2=0.5cm=0.005m
The cross-sectional area (A1) of the first rope is given by:
A1=πR12=π(0.005)2=π×0.000025=7.85×10−5m2
Given that the maximum tension (T1) the first rope can withstand is 500 N, we can calculate the breaking stress (σ) as:
σ=T1A1=500N7.85×10−5m2≈6.37×106N/m2
The diameter of the second rope (D2) is 3 cm, so the radius (R2) is:
R2=D22=3cm2=1.5cm=0.015m
The cross-sectional area (A2) of the second rope is given by:
A2=πR22=π(0.015)2=π×0.000225=7.07×10−4m2
Since the breaking stress remains the same for both ropes (as they are made of the same material), we can set up the equation:
σ=T2A2
Rearranging gives us:
T2=σ×A2
Substituting the values we found:
T2=(6.37×106N/m2)×(7.07×10−4m2)≈4500N
The maximum tension that may be given to the similar rope of diameter 3 cm is approximately 4500 N.
Topper's Solved these Questions
- ELASTICITY BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - MHT CET CORNER
16 Videos
- ELASTICITY BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - EXERCISE 1
66 Videos
- CURRENT ELECTRICITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - MHT CET CONER
34 Videos
Similar Questions
A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that any be given to a similar rope of diameter 2 cm is
View SolutionA wire of diameter 1 mm breaks under a tension of 1000 N. Another wire of same materials as that of the first one but of diameter 2 mm breaks under a tension of
View Solution
Knowledge Check
A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that any be given to a similar rope of diameter 2 cm is
A500 NB250 NC1000 ND2000 NA rope of 1 cm in diameter breaks if tension in it exceeds 500 N the maxmum tension that may be given to a smilar rope of diameter 2 cm is
A500 NB250 NC1000 ND2000 NA nylon rope 2cm in diameter has a breaking strength of 1.5×105N. The breaking strength of a similar rope 1cm in diameter is
A0.375×105NB2×105NC6×105ND9×104N
A wire of diameter 1mm breaks under a tension of 1000 N. Another wire, of same material as that of the first one, but of diameter 2mm breaks under a tension of
View SolutionIf a steel wire of diameter 2 mm has a breaking strength of 4×105N. Then the breaking strength of similar wire of diameter 1 mm will be
View SolutionThe surface tension of a soap solution is 2.1×10−2 N//m . The work done in blowing a soap bubble of diameter 6.0 cm is
View SolutionOne end of a massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum tension that the rope can bear is 360 N. With what value of maximum safe acceleration (in ms−2) can a man of 60kg climb down the rope?
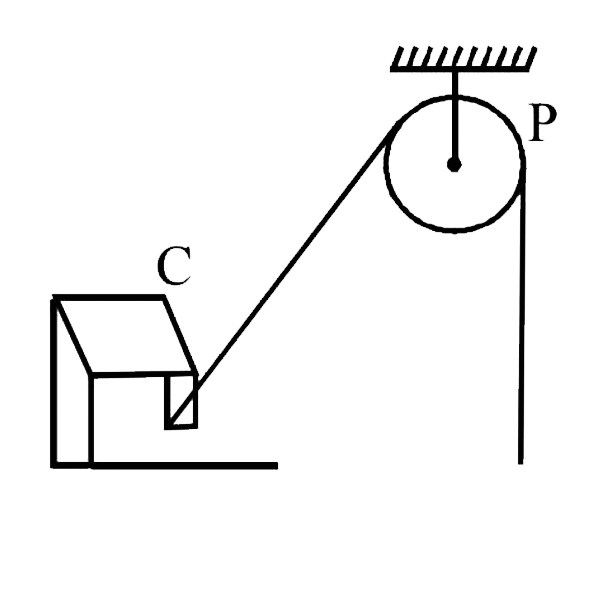
View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View Solution
