Under elastic limit the stess is
indirectly proportional to strain
directly proportional to strain
independent to strain
None of the above
The correct Answer is:b
Hooke's law is applicable.
By Hooke's law, for small deformations.
Tensile stressTensile strain=Y
Is a constant for the given material. This ratio is called Young's modulus.
So. Within elastic limit, the stress developed is directly proportional to the strain produced in a body.
i.e., stress ∝ strain
or stress =E× strain
Topper's Solved these Questions
- ELASTICITY BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - EXERCISE 2
48 Videos
- CURRENT ELECTRICITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - MHT CET CONER
34 Videos
Similar Questions
The elastic limit of stees is 8×108Nm−2 andits Young modulus 2x1011Nm−2. Find the maximum eleongatin of a half metre steel wire that can be given without exceeding the elastic limit.
View SolutionTRUE/FALSE TYPE QUESTIONS Any metallic part of a machinery is never subjected to a stress beyond the elastic limit of the material.
View Solution
Knowledge Check
Within the elastic limit, stress is directly proportional to strain produced in a body is the statement of
ARobert's lawBHooke's lawCNewton's lawDBoyle's lawWithin the elastic limit, the ratio of shear stress and shearing strain is called
AYBKCηDσAccording to Hooke's law, within the elastic limit stress/strain = constant. This constant depends on the type of strain or the type of force acting. Tensile stress might result in compressional or elongative strain, however, a tangential stress can only cause a shearing strain. After crossing the elastic limit, the material undergoes elongation and beyond a stage beaks. All modulus of elasticity are basically constants for the materials under stress.
If stress/strain is x in elastic region and y in the region of yield, thenAx=yBx>yCx<yDx=2y
The property of metals which allows to form a thin wires beyond their elastic limit without rupture is
View SolutionThe property of metals where by they could be drawn into thin wires beyond their elastic limit without breaking is
View SolutionWhen the stress is increased beyond the elastic limit, the length of the wire starts increasing without increasing the force. This point is called
View SolutionThe stain-stress curves of three wires of different material are showm in the figure P,Q,R are the elastic limits of the wires, the figure shows that
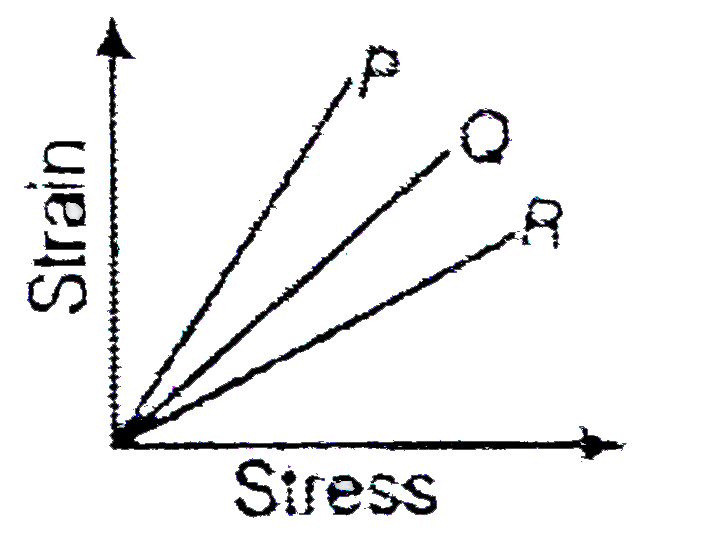
View SolutionA wire is progressively loaded slightly beyond the elastic limit and then the load is completely removed. It is found that a small strain remains in the wire. This small strain is known as
View Solution
