The rate of flow of liquid through a capillary tube of radius r is V, when the pressure difference across the two ends of the capillary is p. If pressure is increased by 3p and radius is reduced to r/2, then the rate of flow becomes
V/9
3V/8
V/4
V/3
The correct Answer is:C
To solve the problem step by step, we will use the principles of fluid dynamics, particularly Poiseuille's law, which relates the flow rate of a liquid through a capillary tube to the pressure difference, the radius of the tube, and the viscosity of the liquid.
Step 1: Understand the initial conditions
We are given:
- Initial flow rate V
- Initial pressure difference P
- Initial radius r
According to Poiseuille's law, the flow rate V through a capillary tube can be expressed as:
V=k⋅Pr4
where k is a constant that depends on the viscosity of the liquid and the length of the tube.
Step 2: Determine the new conditions
Now, the pressure is increased by 3P, making the new pressure difference:
P′=P+3P=4P
The radius is reduced to r2.
Step 3: Write the new flow rate equation
Using the same formula for the new conditions, the new flow rate V′ can be expressed as:
V′=k⋅P′(r′)4
Substituting the new values:
V′=k⋅4P(r2)4
Step 4: Simplify the expression for the new radius
Calculating (r2)4:
(r2)4=r416
Thus, we can rewrite the new flow rate as:
V′=k⋅4Pr416=k⋅4P⋅16r4=k⋅64Pr4
Step 5: Relate the new flow rate to the initial flow rate
Since the initial flow rate V is given by:
V=k⋅Pr4
We can express the new flow rate V′ in terms of V:
V′=64⋅Pr4⋅k=64⋅V
Step 6: Finalize the answer
Thus, the new flow rate V′ is:
V′=64V
Conclusion
The new rate of flow becomes 64V.
---
We are given:
- Initial flow rate V
- Initial pressure difference P
- Initial radius r
V=k⋅Pr4
where k is a constant that depends on the viscosity of the liquid and the length of the tube.
Now, the pressure is increased by 3P, making the new pressure difference:
P′=P+3P=4P
The radius is reduced to r2.
Using the same formula for the new conditions, the new flow rate V′ can be expressed as:
V′=k⋅P′(r′)4
Substituting the new values:
V′=k⋅4P(r2)4
Calculating (r2)4:
(r2)4=r416
Thus, we can rewrite the new flow rate as:
V′=k⋅4Pr416=k⋅4P⋅16r4=k⋅64Pr4
Since the initial flow rate V is given by:
V=k⋅Pr4
We can express the new flow rate V′ in terms of V:
V′=64⋅Pr4⋅k=64⋅V
Thus, the new flow rate V′ is:
V′=64V
The new rate of flow becomes 64V.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner15videos
SURFACE TENSION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - Exercise 130videos
SURFACE TENSION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner28videos
STATIONARY WAVES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE MOTIONEXERCISE - MHT CET CORNER23videos
WAVE MOTION
Similar Questions
Water flows in a stream line manner through a capillary tube of radius a. The pressure difference being P and the rate of flow is Q. If the radius is reduced to a4 and the pressure is increased to 4P. then the rate of flow becomes
View SolutionWhen water flows at a rate Q through a capillary tube of radius r placed horizontally a pressure difference p develops across the ends of the tube. If the radius of the tube is doubled and the rate of flow halved the pressure difference becomes
View Solution
Knowledge Check
- Question 1 - Select One
The rate of flow of a liquid through a capillary tube is
Adirectly proportional to the length of tube.Binversely proportional to the difference of pressure between the ends of the tube.Cdirectly proportional to the 4th power of the radius of the tube.Dindependent of the nature of the liquid. - Question 2 - Select One
Water flows in a stream line manner through a capillary tube of radius a. the pressure difference being P and the rate of the flows is Q. If the radius is reduced to a4 and the pressure is increased to 4P, then the rate of flow becomes
AQ2=64QBQ2=Q/64CQ2=Q/32DQ2=Q/16 - Question 3 - Select One
The rate of flow of liquid through a capillary tube in an experiment to determine the viscosity of the liquid increases
Awhen the pressure of the tube is increasedBwhen the length of the tube is increasedCwhen the radius of the tube is decreasedDnone of the above
Water flows in a streamline manner through a cappilary tube of radius a. The pressure difference being P and the rate of flow is Q . If the radius is reduced to a/2 and the pressure difference is increased to 2P, then find the rate of flow.
View SolutionThe rate of flow of liquid through a capillary tube of length l and radius r is Q at a constant pressure p. The rate of flow of liquid through a capillary tube of radius r2 and length 21 at the same pressure head will be_____
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
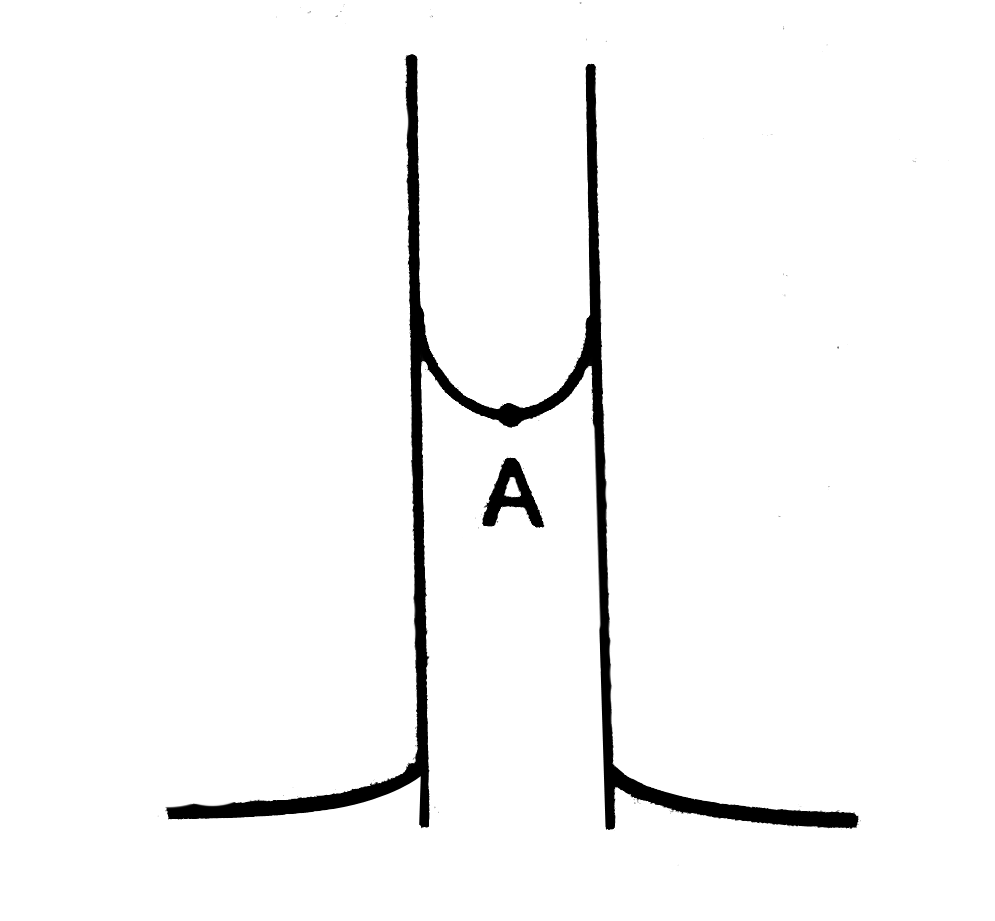 View Solution
View SolutionIf Q is the rate of flow of liquid through a capillary tube of length l and radius r at constant pressure P, then the rate of flow of liquid through a capillary head is
View SolutionThe rate of flow of liquid ina tube of radius r, length l, whose ends are maintained at a pressure difference P is V=πQPr4ηl where η is coefficient of the viscosity and Q is
View Solution

