The vibrating of four air columns are represented in
the figure. The ratio of frequencies np:nq:nr:ns is
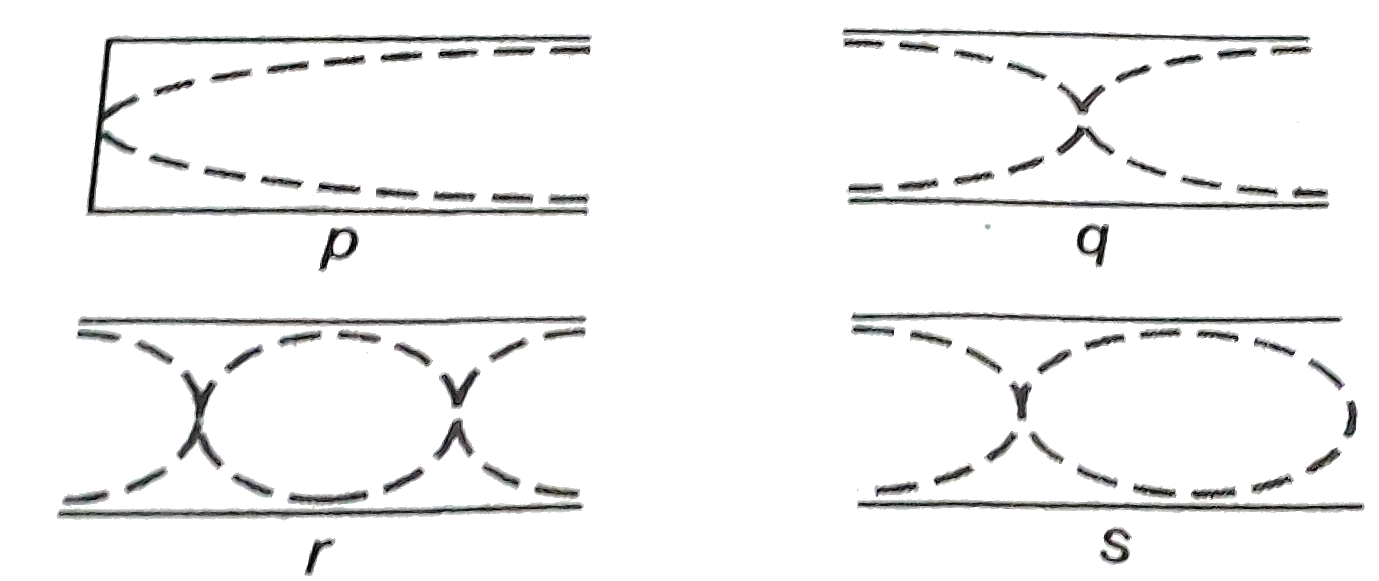
12:6:3:5
1:2:4:3
4:2:3:1
6:2:3:4
The correct Answer is:b
As it is clear from figure of question,
l=λp4,λp=4l,np=vλp=v4l
l=λp4,λq=2l,nq=vλq=v2l
l=λr,λr=1,nr=vλr=vl
l=3λs4,λs=4l3,ns=vλs=3v4l
∴np:nq:nr:ns=v4l:v2l:vl:3vl=1:2:4:3
Topper's Solved these Questions
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - EXERCISE 2
27 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- SEMICONDUCTORSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEMICONDUCTORSEXERCISE - MHT CET Corner
25 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
Similar Questions
Knowledge Check
The vibrations of four air columns are represented in the figure below. The ratio of frequencies np:nq:nr:ns is
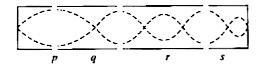 A12:6:3:4B1:2:4:3C4:2:3:1D6:2:3:4
A12:6:3:4B1:2:4:3C4:2:3:1D6:2:3:4The vibrations of four air columns are represented in the adjoining figures. The ratio of frequencies np:nq:nr:ns is
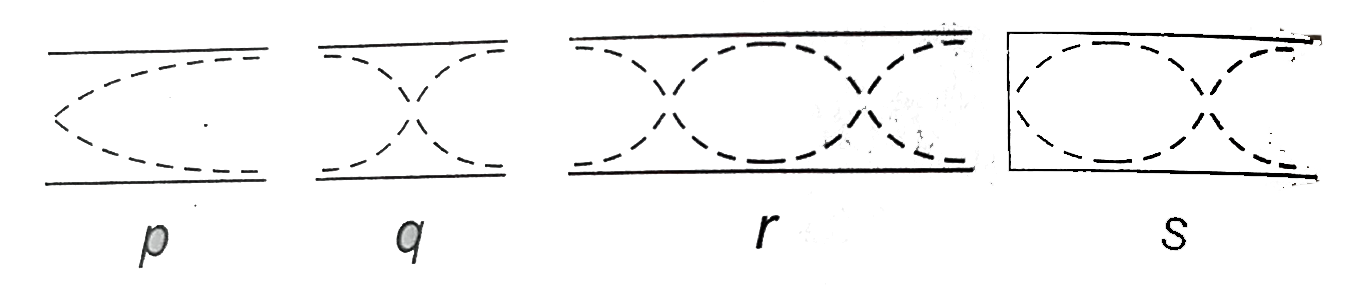 A12:6:3:4B4:2:3:1C1:2:4:3D1:2:3:4
A12:6:3:4B4:2:3:1C1:2:4:3D1:2:3:4Figures shows the vibrations of foue air columns. The ratio of frequencies np:nq:nr:ns is
 A12:3:3:4B1:2:4:3C4:2:3:1D4:3:2:1
A12:3:3:4B1:2:4:3C4:2:3:1D4:3:2:1
The vibrations of four air columns under identical conditions are represented in the figure below. The ratio of frequencies np:nq:nr:ns will be
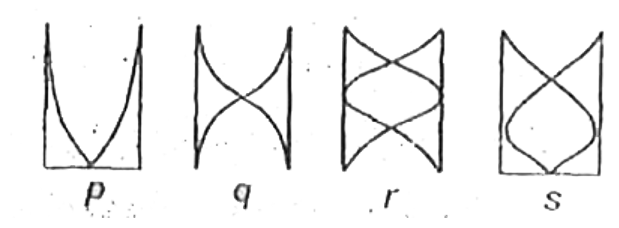
View SolutionFigures shows the vibrations of four air column. The ratio of frequencies np:nq:nr:ns is

View SolutionThe frequency of vibration of air column in a pipe closed at one end is n1and that of the one closed at both end is n2. When both the pipes are joined to form a pipe closed atone end, the frequency of vibration of air column in it is (neglecting end correction )
View SolutionA string A has double the length, double the tension, double the diameter and double the density as another string B. Their fundamental frequencies of vibration are nA and nB respectively. The ratio nA/nB is equal to
View SolutionTwo vibrating strings of the same material but lengths L and 2L have radii 2r and r respectively. They are stretched under the same tension. Both the strings vibrate in their fundamental modes, the one of length L with frequency n1 and the other with frequency n2 the ratio n1/n2 is given by
View Solution
